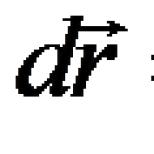Matris türleri ve özellikleri. Matrislerde temel işlemler. İki matrisi çarpma işleminin tanımı

Matrislerde işlemlerin bazı özellikleri.
matris ifadeleri

Ve şimdi, sadece yeni materyalleri değil, aynı zamanda üzerinde çalışacağımız konunun devamı gelecek. matris işlemleri.

Matrislerdeki işlemlerin bazı özellikleri

Matrislerle işlemlerle ilgili pek çok özellik vardır, aynı Wikipedia'da ilgili kuralların ince sıralarına hayran olabilirsiniz. Bununla birlikte, pratikte, gerçek problemlerin çözümü sırasında sadece bazıları kullanıldığından, birçok özellik bir anlamda "ölüdür". Amacım somut örneklerle özelliklerin uygulanmasına bakmak ve titiz bir teoriye ihtiyacınız varsa, lütfen başka bir bilgi kaynağı kullanın.

biraz düşünün kuralın istisnaları pratik görevleri yerine getirmek için gereklidir.

Bir kare matris varsa ters matris, o zaman çarpmaları değişmeli:

kimlik matrisi ile kare matris denir ana köşegen birimler bulunur ve kalan elemanlar sıfıra eşittir. Örneğin: , vb.

nerede aşağıdaki özellik doğrudur: keyfi bir matris çarpılırsa sol veya sağ uygun boyutlarda bir kimlik matrisi ile, sonuç orijinal matristir:

Gördüğünüz gibi, matris çarpımının değişebilirliği de burada gerçekleşir.

Biraz matris alalım, peki, diyelim ki önceki problemin matrisi: .

İlgilenenler şunları kontrol edebilir ve şunlardan emin olabilir:

Matrisler için kimlik matrisi, özellikle az önce ele alınan örneklerden açıkça görülen, sayılar için sayısal birimin bir analogudur.

Matris çarpımına göre sayısal bir faktörün değiştirilebilirliği

Aşağıdaki özellik matrisler ve gerçek sayılar için geçerlidir:

Yani, sayısal faktör, matrislerin çarpımına "karışmaması" için ileriye doğru hareket ettirilebilir (ve edilmelidir).

Not : Genel olarak, özelliğin ifadesi eksiktir - "lambda" matrislerin arasına herhangi bir yere, hatta sonuna yerleştirilebilir. Üç veya daha fazla matris çarpılırsa kural geçerliliğini korur.

Örnek 4

Ürün Hesapla

Karar:

(1) Mülkiyete göre sayısal faktörü ileri doğru hareket ettirin. Matrislerin kendileri yeniden düzenlenemez!

(2) - (3) Matris çarpımı gerçekleştirin.

(4) Burada her bir sayıyı 10'a bölebilirsiniz, ancak daha sonra matrisin öğeleri arasında ondalık kesirler görünecektir, bu iyi değildir. Bununla birlikte, matristeki tüm sayıların 5'e bölünebildiğini fark ettik, bu yüzden her elemanı .

Cevap:

Kendi başınıza çözmek için küçük bir maskaralık:

Örnek 5

Eğer hesapla

Çözüm ve cevap dersin sonunda.

Bu tür örnekleri çözmek için hangi teknik önemlidir? sayılarla uğraşmak geçen .

Lokomotife bir vagon daha bağlayalım:

Üç matris nasıl çarpılır?

Her şeyden önce, üç matrisin çarpılmasının sonucu NE olmalıdır? Kedi fare doğurmaz. Matris çarpımı mümkünse, sonuç da bir matris olacaktır. Cebirsel yapının elemanlarına göre kapalılığını nasıl açıkladığımı cebir hocam görmüyor =)

Üç matrisin çarpımı iki şekilde hesaplanabilir:

1) "ce" matrisini bulun ve bununla çarpın: ;

2) önce bulun, ardından çarpma işlemini gerçekleştirin.

Sonuçlar mutlaka çakışacaktır ve teoride bu özelliğe matris çarpımının ilişkiselliği denir:

Örnek 6

Matrisleri iki şekilde çarpma

algoritma çözümler iki adımlı: iki matrisin çarpımını bulun, sonra tekrar iki matrisin çarpımını bulun.

1) formülü kullanın

Birinci işlem:

Eylem iki:

2) formülü kullanın

Birinci işlem:

Eylem iki:

Cevap:

Elbette daha tanıdık ve standart olan, orada "sanki her şey yolundaymış gibi" çözmenin ilk yoludur. Bu arada, sipariş hakkında. İncelenen görevde, genellikle bir tür matris permütasyonundan bahsettiğimiz yanılsaması ortaya çıkar. Burada değiller. tekrar hatırlatırım Genel olarak MATRİSLERİ DEĞİŞTİRMEYİN. Yani ikinci paragrafta ikinci adımda çarpma işlemi yapıyoruz ama hiçbir durumda yapmıyoruz. Sıradan sayılarla böyle bir sayı geçer, ancak matrislerle olmaz.

Çarpmanın birleştirilebilirlik özelliği sadece kare için değil, aynı zamanda keyfi matrisler için de geçerlidir - eğer sadece çarpılırlarsa:

Örnek 7

Üç matrisin ürününü bulun

Bu bir kendin yap örneğidir. Örnek çözümde hesaplamalar iki şekilde gerçekleştirilmiştir, hangi yolun daha karlı ve daha kısa olduğu analiz edilmiştir.

Matris çarpımının birleştirilebilirlik özelliği, daha fazla sayıda faktör için gerçekleşir.

Şimdi matrislerin güçlerine dönme zamanı. Matrisin karesi en başta düşünülür ve gündemdeki soru şudur:

Bir matris ve daha yüksek güçler nasıl küplenir?

Bu işlemler de sadece kare matrisler için tanımlanmıştır. Bir kare matrisi bir küp haline getirmek için ürünü hesaplamanız gerekir:

Aslında bu, matris çarpımının çağrışım özelliğine göre üç matrisin çarpılmasının özel bir durumudur: . Ve kendisiyle çarpılan bir matris, matrisin karesidir:

Böylece, çalışma formülünü elde ederiz:

Yani görev iki adımda gerçekleştirilir: ilk önce matrisin karesi alınmalı ve ardından ortaya çıkan matris matris ile çarpılmalıdır.

Örnek 8

Matrisi bir küp haline getirin.

Bu, kendi başınıza çözmeniz gereken küçük bir sorundur.

Bir matrisi dördüncü güce yükseltmek doğal bir şekilde gerçekleştirilir:

Matris çarpımının ilişkilendirilebilirliğini kullanarak, iki çalışma formülü elde ederiz. Birincisi: üç matrisin ürünüdür.

1) . Başka bir deyişle, önce buluruz, sonra onu “olmak” ile çarparız - bir küp alırız ve son olarak çarpmayı tekrar yaparız - dördüncü derece olacaktır.

2) Ama bir adım daha kısa bir çözüm var: . Yani, ilk adımda kareyi buluyoruz ve küpü atlayarak çarpma işlemini gerçekleştiriyoruz.

Örnek 8'e ek görev:

Matrisi dördüncü güce yükseltin.

Az önce belirtildiği gibi, bu iki şekilde yapılabilir:

1) Küp bilinir bilinmez çarpma işlemi yaparız.

2) Ancak, sorunun durumuna göre bir matris oluşturulması gerekiyorsa, sadece dördüncü derecede, o zaman yolu kısaltmak avantajlıdır - matrisin karesini bulun ve formülü kullanın .

Hem çözümler hem de cevap dersin sonunda.

Benzer şekilde, matris beşinci ve daha yüksek güçlere yükseltilir. Pratik deneyimlerden, bazen 4. dereceye yükseltme örnekleri olduğunu söyleyebilirim, ancak beşinci dereceden bir şey hatırlamıyorum. Ama her ihtimale karşı en uygun algoritmayı vereceğim:

1) bul;
2) bul;
3) matrisi beşinci güce yükseltin: .

Burada, belki de, pratik problemlerde faydalı olabilecek matris işlemlerinin tüm ana özellikleri verilmiştir.

Dersin ikinci bölümünde daha az renkli bir parti beklenmiyor.

matris ifadeleri

Her zamanki okul ifadelerini sayılarla tekrarlayalım. Sayısal bir ifade sayılardan, matematiksel sembollerden ve parantezlerden oluşur, örneğin: . Hesaplamalarda, bilinen cebirsel öncelik geçerlidir: ilk olarak, parantez, ardından idam edildi üs alma / köklerin çıkarılması, sonrasında çarpma / bölme ve son olarak - Ekleme çıkarma.

Sayısal bir ifade anlamlıysa, değerlendirmesinin sonucu bir sayıdır., Örneğin:

matris ifadeleri neredeyse tamamen aynı! Ana aktörlerin matrisler olması farkıyla. Ayrıca, bir matrisin yer değiştirmesi ve tersinin bulunması gibi bazı belirli matris işlemleri.

Matris ifadesini düşünün , bazı matrisler nerede. Bu matris ifadesinin üç terimi vardır ve toplama/çıkarma işlemleri en son yapılır.

İlk terimde, önce "be": matrisini transpoze etmeniz, ardından çarpma işlemini gerçekleştirmeniz ve elde edilen matrise "iki" eklemeniz gerekir. Bunu not et devrik işlemi çarpma işleminden daha yüksek önceliğe sahiptir. Parantezler, sayısal ifadelerde olduğu gibi, eylemlerin sırasını değiştirir: - burada, önce çarpma yapılır, ardından ortaya çıkan matris aktarılır ve 2 ile çarpılır.

İkinci terimde ilk önce matris çarpımı yapılır ve ters matris zaten üründen bulunur. Parantezler kaldırılırsa: önce ters matrisi bulmanız ve ardından matrisleri çarpmanız gerekir: . Ters matrisi bulmak da çarpmaya göre önceliklidir.

Üçüncü terim ile her şey açıktır: matrisi bir küp haline getiriyoruz ve ortaya çıkan matrise “beş” i ekliyoruz.

Matris ifadesi mantıklıysa, değerlendirmesinin sonucu bir matristir..

Tüm görevler gerçek testlerden olacak ve en basitinden başlayacağız:

Örnek 9

matris verileri . Bulmak:

Karar: işlem sırası bellidir, önce çarpma, sonra toplama yapılır.

Matrisler farklı boyutlarda olduğu için toplama yapılamamaktadır.

Şaşırmayın, bu tür görevlerde genellikle imkansız eylemler sunulur.

İkinci ifadeyi hesaplamaya çalışalım:

Burada her şey iyi.

Cevap: eylem gerçekleştirilemez, .

matrisler. Matrisler üzerindeki işlemler. Matrisler üzerinde işlemlerin özellikleri. Matris türleri.

Matrisler (ve buna göre matematiksel bölüm - matris cebiri) Nesnelerin ve süreçlerin matematiksel modellerinin önemli bir bölümünü oldukça basit bir biçimde yazmaya izin verdikleri için uygulamalı matematikte önemlidir. "Matris" terimi 1850'de ortaya çıktı. Matrislerden ilk olarak antik Çin'de, daha sonra Arap matematikçiler tarafından bahsedildi.

Matris A=Amn sipariş m*n denir m - satır ve n - sütun içeren dikdörtgen sayılar tablosu.

matris öğeleri aij , bunun için i=j köşegen olarak adlandırılır ve ana köşegen.

Bir kare matris (m=n) için, ana köşegen a 11 , a 22 ,..., a nn öğelerinden oluşur.

Matris eşitliği.

A=B, eğer matris siparişleri A ve B aynılar ve a ij =b ij (i=1,2,...,m; j=1,2,...,n)

Matrisler üzerindeki işlemler.

1. Matris ekleme - eleman bazında işlem

2. Matris çıkarma - eleman işlemiyle eleman

3. Bir matrisin bir sayı ile çarpımı, eleman eleman bir işlemdir.

4. Çarpma A*B kurala göre matrisler sütun başına satır(A matrisinin sütun sayısı, B matrisinin satır sayısına eşit olmalıdır)

A mk *B kn =C mn ve her eleman ij ile matrisler cmn A matrisinin i-inci satırının elemanlarının, B matrisinin j-inci sütununun karşılık gelen elemanları ile çarpımlarının toplamına eşittir, yani.

Bir örnek kullanarak matris çarpma işlemini gösterelim

5. üs alma

m>1 pozitif bir tamsayıdır. A bir kare matristir (m=n) yani. sadece kare matrisler için geçerlidir

6. A matrisinin aktarılması. Aktarılan matris, AT veya A olarak gösterilir "

Satırlar ve sütunlar değiştirilir

Misal

Matrislerdeki işlemlerin özellikleri

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(λA)"=λ(A)"

(A+B)"=A"+B"

(AB)"=B"A"

matris türleri

1. Dikdörtgen: m ve n- keyfi pozitif tam sayılar

2. Kare: m=n

3. Matris satırı: m=1. Örneğin, (1 3 5 7) - birçok pratik problemde böyle bir matrise vektör denir

4. Matris sütunu: n=1. örneğin

5. Köşegen Matris: m=n ve bir ij =0, Eğer i≠j. örneğin

6. Kimlik matrisi: m=n ve

7. Sıfır matrisi: a ij =0, i=1,2,...,m

j=1,2,...,n

8. Üçgen matris: ana köşegenin altındaki tüm elemanlar 0'dır.

9. Simetrik matris: m=n ve aij=aji(yani, ana köşegene göre simetrik olan yerlerde eşit elemanlar vardır) ve bu nedenle A"=A

Örneğin,

10. Eğrilik matrisi: m=n ve bir ij = -a ji(yani zıt elemanlar ana köşegene göre simetrik olan yerlerde durur). Bu nedenle, ana köşegen üzerinde sıfırlar vardır (çünkü ben=j sahibiz bir ii =-a ii)

Apaçık, A"=-A

11. Hermit matrisi: m=n ve a ii =-ã ii (ı ji- karmaşık - eşlenik bir ji, yani Eğer A=3+2i, daha sonra karmaşık eşlenik Ã=3-2i)

Bu yazımızda aynı sıradaki matrisler üzerinde toplama işleminin nasıl yapıldığını, bir matrisin bir sayı ile çarpma işlemini ve uygun sıradaki matrisleri çarpma işlemini anlayacağız, işlemlerin özelliklerini aksiyomatik olarak ayarlayacağız, ve ayrıca matrislerdeki işlemlerin önceliğini tartışın. Teoriye paralel olarak matrisler üzerinde işlemlerin yapıldığı örneklere detaylı çözümler vereceğiz.

Aşağıdakilerin tümünün, öğeleri gerçek (veya karmaşık) sayılar olan matrisler için geçerli olduğunu hemen belirtelim.

Sayfa gezintisi.

İki matris toplama işlemi.

İki matris toplama işleminin tanımı.

Toplama işlemi SADECE AYNI DÜZEYDEKİ MATRİSLER İÇİN tanımlanır. Başka bir deyişle, farklı boyutlardaki matrislerin toplamını bulmak imkansızdır ve genel olarak farklı boyutlardaki matrislerin toplamından bahsetmek imkansızdır. Ayrıca, bir matrisin ve bir sayının toplamından veya bir matrisin ve başka bir elemanın toplamından bahsedilemez.

Tanım.

iki matrisin toplamı ve elemanları A ve B matrislerinin karşılık gelen elemanlarının toplamına eşit olan bir matristir, yani .

Böylece, iki matrisi toplama işleminin sonucu aynı sıradaki bir matristir.

Matris toplama işleminin özellikleri.

Matris toplama işleminin özellikleri nelerdir? Belirli bir sıradaki iki matrisin toplamının tanımından başlayarak ve gerçek (veya karmaşık) sayıların toplama işleminin özelliklerini hatırlayarak bu soruyu cevaplamak oldukça kolaydır.

1. Aynı sıradaki A, B ve C matrisleri için, toplamanın birleştirilebilirlik özelliği, A + (B + C) \u003d (A + B) + C karakteristiğidir.
2. Belirli bir sıradaki matrisler için, sıfır matrisi olan toplamaya göre nötr bir eleman vardır. Yani, A + O \u003d A özelliği doğrudur.
3. Belirli bir sıradaki sıfır olmayan bir A matrisi için bir matris vardır (-A ), toplamları sıfır matristir: A + (-A) \u003d O .
4. Belirli bir sıradaki A ve B matrisleri için, A+B=B+A toplamasının değişme özelliği geçerlidir.

Sonuç olarak, belirli bir sıradaki matrisler kümesi, toplamalı bir Abel grubu (cebirsel toplama işlemine göre bir Değişken grup) oluşturur.

Matris ekleme - çözme örnekleri.

Şimdi bazı matris toplama örneklerine bakalım.

Misal.

Matrislerin toplamını bulun ve .

Karar.

A ve B matrislerinin mertebeleri aynı ve 4'e 2'ye eşittir, bu yüzden matris toplama işlemini yapabiliriz ve sonuç olarak 4'e 2 mertebesinde bir matris almalıyız. İki matris ekleme işleminin tanımına göre, eleman eleman toplama işlemini gerçekleştiririz:

Misal.

İki matrisin toplamını bulun ve elemanları karmaşık sayılardır.

Karar.

Matris sıraları eşit olduğu için toplama işlemi yapabiliriz.

Misal.

Üç matrisin eklenmesini gerçekleştirin .

Karar.

Önce A matrisini B ile ekleyin, ardından elde edilen matrise C ekleyin:

Sıfır matrisimiz var.

Bir matrisi bir sayı ile çarpma işlemi.

Bir matrisi bir sayı ile çarpma işleminin tanımı.

Bir matrisi bir sayı ile çarpma işlemi HERHANGİ BİR DÜZENLİ MATRİSLER İÇİN tanımlanır.

Tanım.

Bir matris ve bir gerçek (veya karmaşık) sayının çarpımı elemanları orijinal matrisin karşılık gelen elemanlarının bir sayı ile çarpılmasıyla elde edilen bir matristir, yani .

Böylece, bir matrisin bir sayı ile çarpılmasının sonucu aynı dereceden bir matristir.

Bir matrisi bir sayı ile çarpma işleminin özellikleri.

Bir matrisi bir sayı ile çarpma işleminin özelliklerinden, sıfır matrisini sıfırla çarpmanın sıfır matrisi vereceğini ve keyfi bir sayı ile sıfır matrisinin ürününün bir sıfır matrisi olduğunu takip eder.

Bir matrisin bir sayı ile çarpımı - örnekler ve çözümleri.

Örnekler kullanarak bir matrisi bir sayı ile çarpma işlemini ele alalım.

Misal.

2 sayısı ile matrisin çarpımını bulun .

Karar.

Bir matrisi bir sayı ile çarpmak için, elemanlarının her birini şu sayı ile çarpmanız gerekir:

Misal.

Bir sayı ile matris çarpımı gerçekleştirin.

Karar.

Verilen matrisin her elemanını verilen sayı ile çarpıyoruz:

İki matrisi çarpma işlemi.

İki matrisi çarpma işleminin tanımı.

İki A ve B matrisini çarpma işlemi yalnızca, A MATRİSİNİN SÜTUN SAYISI B MATRİSİNİN SATIR SAYISINA EŞİT olduğunda tanımlanır.

Tanım.

A mertebesinde bir matrisin ve mertebeden bir B matrisinin çarpımı- bu, her bir elemanı, matris A'nın i-inci satırının elemanlarının çarpımlarının toplamına, B matrisinin j-inci sütununun karşılık gelen elemanlarına eşit olan böyle bir C matrisidir, yani ,

Böylece bir sıra matrisinin bir sıra matrisi ile çarpılması işleminin sonucu bir sıra matrisidir.

Bir matrisin bir matrisle çarpımı - örneklerin çözümleri.

Örnekler kullanarak matris çarpımını ele alacağız, ardından matris çarpım işleminin özelliklerini listelemeye geçeceğiz.

Misal.

Matrislerin çarpılmasıyla elde edilen C matrisinin tüm elemanlarını bulun ve .

Karar.

A matrisinin mertebesi n=2'ye göre p=3'tür, B matrisinin mertebesi n=2'ye q=4'tür, dolayısıyla bu matrislerin çarpımının sırası p=3'e q=4'tür. formülü kullanalım

Sırayla, 1'den 4'e ( q=4'ten beri) her j için 1'den 3'e (p=3'ten beri) i ​​değerleri alıyoruz ve bizim durumumuzda n=2, o zaman

C matrisinin tüm elemanları bu şekilde hesaplanır ve verilen iki matrisin çarpılmasıyla elde edilen matris şu şekildedir: .

Misal.

Matris çarpımı gerçekleştirin ve .

Karar.

Orijinal matrislerin sıraları çarpma işlemini gerçekleştirmemizi sağlar. Sonuç olarak, 2'ye 3 mertebeden bir matris almalıyız.

Misal.

Verilen matrisler ve . A ve B matrislerinin yanı sıra B ve A matrislerinin çarpımını bulun.

Karar.

A matrisinin mertebesi 3'e 1 ve matris B'nin mertebesi 1'e 3 olduğundan, A⋅B 3'e 3 mertebesine sahip olacak ve B ve A matrislerinin çarpımı 1'e 1 mertebesine sahip olacaktır.

Gördüğünüz gibi, . Bu, matris çarpma işleminin özelliklerinden biridir.

Matris çarpım işleminin özellikleri.

A, B ve C matrisleri uygun mertebeden ise, aşağıdakiler doğrudur. matris çarpma işleminin özellikleri.

Uygun mertebeler için sıfır matrisi O ve matris A'nın çarpımının bir sıfır matrisi verdiğine dikkat edilmelidir. A'nın O'ya çarpımı, siparişler matris çarpma işlemine izin veriyorsa, sıfır matrisi verir.

Kare matrisler arasında sözde vardır permütasyon matrisleri, onlar için çarpma işlemi değişmeli, yani . Permütasyon matrislerine bir örnek, bir birim matris çifti ve aynı sıradaki herhangi bir başka matristir, çünkü .

Matrislerde işlemlerin önceliği.

Bir matrisi bir sayı ile çarpma ve bir matrisi bir matrisle çarpma işlemleri eşit önceliğe sahiptir. Aynı zamanda, bu işlemler iki matris ekleme işleminden daha yüksek önceliğe sahiptir. Böylece önce matris sayı ile çarpılır ve matrisler çarpılır ve ancak o zaman matrisler toplanır. Bununla birlikte, matrisler üzerinde işlemlerin gerçekleştirilme sırası parantezler kullanılarak açıkça belirtilebilir.

Bu nedenle, matrislerdeki işlemlerin önceliği, gerçek sayıların toplama ve çarpma işlemlerine atanan önceliğe benzer.

Misal.

matris verileri . Verilen matrislerle belirtilen eylemleri gerçekleştirin .

Karar.

A matrisini B matrisiyle çarparak başlıyoruz:

Şimdi ikinci dereceden kimlik matrisi E'yi iki ile çarpıyoruz:

Elde edilen iki matrisi ekliyoruz:

Elde edilen matrisi A matrisi ile çarpma işlemini gerçekleştirmek için kalır:

Aynı A ve B mertebesine sahip matrislerin çıkarılması işleminin bu şekilde mevcut olmadığına dikkat edilmelidir. İki matrisin farkı esasen A matrisi ile B matrisinin ön çarpımının eksi bir ile çarpımıdır: .

Bir kare matrisi doğal bir güce yükseltme işlemi, matrislerin ardışık bir çarpımı olduğundan bağımsız değildir.

Özetle.

Matrisler kümesi üzerinde üç işlem tanımlanmıştır: aynı dereceden matrislerin toplanması, bir matrisin bir sayı ile çarpımı ve uygun dereceli matrislerin çarpımı. Belirli bir sıradaki bir dizi matris üzerindeki toplama işlemi, bir Abel grubu oluşturur.

matrisler. Matris türleri. Matrisler ve özellikleri üzerinde işlemler.

n. dereceden matrisin determinantı. N, Z, Q, R, C,

m*n düzeyindeki bir matris, m satırları ve n sütunları içeren dikdörtgen bir sayı tablosudur.

Matris eşitliği:

Birinin satır ve sütun sayısı sırasıyla diğerinin satır ve sütun sayısına eşitse, iki matris eşit olarak adlandırılır. bu matrislerin elemanları eşittir.

Not: Aynı dizinlere sahip öğeler eşleştirilir.

Matris türleri:

Kare Matris: Satır sayısı sütun sayısına eşitse bir matrisin kare olduğu söylenir.

Dikdörtgen: Satır sayısı sütun sayısına eşit değilse bir matrisin dikdörtgen olduğu söylenir.

Satır matrisi: 1*n (m=1) düzeyindeki bir matris a11,a12,a13 biçimindedir ve satır matrisi olarak adlandırılır.

Matris sütunu:………….

Köşegen: Sol üst köşeden sağ alt köşeye giden, yani a11, a22 ...... - öğelerinden oluşan kare matrisin köşegenine ana köşegen denir. (tanım: ana köşegen üzerinde bulunanlar hariç tüm elemanları sıfıra eşit olan bir kare matrise köşegen matris denir.

Kimlik: Tüm elemanlar ana köşegen üzerinde bulunuyorsa ve 1'e eşitse, bir köşegen matrise kimlik denir.

Üst üçgen: A=||aij|| aij=0 ise üst üçgen matris olarak adlandırılır. Sağlanan i>j.

Alt üçgen: aij=0. ben

Sıfır: Bu, El'leri 0 olan bir matristir.

Matrisler üzerinde işlemler.

1. Aktarım.

2. Bir matrisin bir sayı ile çarpımı.

3. Matris ekleme.

4. Matris çarpımı.

Matrislerde temel sv-va eylemi.

1.A+B=B+A (değişebilirlik)

2.A+(B+C)=(A+B)+C (çağrışım)

3.a(A+B)=aA+aB (dağıtılabilirlik)

4.(a+b)A=aA+bA (dağıtıcı)

5.(ab)A=a(bA)=b(aA) (asoots.)

6.AB≠BA (iletişim yok)

7.A(BC)=(AB)C (birleştirici) – eğer tanımlıysa yürütülür. Matriks ürünleri yapılır.

8.A(B+C)=AB+AC (dağıtıcı)

(B+C)A=BA+CA (dağıtıcı)

9.a(AB)=(aA)B=(aB)A

Kare matrisin determinantı - tanımı ve özellikleri. Determinantın satır ve sütunlara ayrıştırılması. Belirleyicileri hesaplama yöntemleri.

A matrisinin mertebesi m>1 ise bu matrisin determinantı bir sayıdır.

A matrisinin aij öğesinin cebirsel tümleyeni Aij, sayı ile çarpılan küçük Mij'dir.

TEOREM1: A matrisinin determinantı, rastgele bir satırın (sütun) tüm elemanlarının ve bunların cebirsel tümleyenlerinin çarpımlarının toplamına eşittir.

Determinantların temel özellikleri.

1. Bir matrisin determinantı transpoze edildiğinde değişmez.

2. İki satıra (sütunlara) izin verilirken, determinant işaret değiştirir, ancak mutlak değeri değişmez.

3. İki özdeş satıra (sütunlara) sahip bir matrisin determinantı 0'dır.

4. Bir matrisin bir satırını (sütununu) bir sayı ile çarparken, determinantı bu sayı ile çarpılır.

5. Matrisin satırlarından (sütunlarından) biri 0 ise bu matrisin determinantı 0'dır.

6. Bir matrisin i. satırının (sütununun) tüm öğeleri iki terimin toplamı olarak temsil ediliyorsa, determinantı iki matrisin determinantlarının toplamı olarak gösterilebilir.

7. Sırasıyla bir sütunun (satırın) öğeleri başka bir sütunun (satırın) öğelerine önceden çarpılarak eklenirse determinant değişmeyecektir. aynı numara için.

8. Belirleyicinin herhangi bir sütununun (satırının) rastgele öğelerinin, başka bir sütunun (satırın) öğelerinin karşılık gelen cebirsel tümleyenine toplamı 0'dır.

https://pandia.ru/text/78/365/images/image004_81.gif" width="46" height="27">

Determinantı hesaplama yöntemleri:

1. Tanım veya Teorem ile 1.

2. Üçgen bir forma indirgeme.

Ters matrisin tanımı ve özellikleri. Ters matrisin hesaplanması. Matris denklemleri.

Tanım: n mertebesinde bir kare matris, aynı mertebeden bir A matrisinin tersi olarak adlandırılır ve şu şekilde gösterilir:

A matrisinin ters bir matrise sahip olması için, A matrisinin determinantının 0'dan farklı olması gerekli ve yeterlidir.

Ters Matris Özellikleri:

1. Teklik: Belirli bir A matrisi için tersi benzersizdir.

2. matris determinantı

3. Transpozisyon alma ve ters matris alma işlemi.

Matris denklemleri:

A ve B aynı sıradaki iki kare matris olsun.

https://pandia.ru/text/78/365/images/image008_56.gif" width="163" height="11 src=">

Matris kolonlarının lineer bağımlılığı ve bağımsızlığı kavramı. Kolon sisteminin lineer bağımlılığı ve lineer bağımsızlığının özellikleri.

А1,А2…An sütunları, bunların 0. sütuna eşit önemsiz olmayan bir doğrusal kombinasyonu varsa, doğrusal bağımlı olarak adlandırılır.

А1,А2…An sütunları, bunların 0. sütuna eşit önemsiz olmayan bir doğrusal kombinasyonu varsa, doğrusal olarak bağımsız olarak adlandırılır.

Tüm katsayılar С(l) 0'a eşitse, doğrusal bir kombinasyon önemsiz olarak adlandırılır ve aksi takdirde önemsiz değildir.

https://pandia.ru/text/78/365/images/image010_52.gif" width="88" height="24">

2. Sütunların lineer bağımlı olabilmesi için bazı kolonların diğer kolonların lineer birleşimi olması gerekli ve yeterlidir.

Sütunlardan 1 tanesi https://pandia.ru/text/78/365/images/image014_42.gif" width="13" height="23 src="> diğer sütunların doğrusal bir birleşimi olsun.

https://pandia.ru/text/78/365/images/image016_38.gif" width="79" height="24"> doğrusal olarak bağımlıdır, bu durumda tüm sütunlar doğrusal olarak bağımlıdır.

4. Bir kolon sistemi lineer bağımsız ise, o zaman onun alt sistemlerinden herhangi biri de lineer bağımsızdır.

(Sütunlar hakkında söylenenler satırlar için de geçerlidir).

Matris küçükleri. Temel küçükler. Matris sıralaması. Bir matrisin sırasını hesaplamak için küçükleri kenarda bırakma yöntemi.

A matrisinin mertebesi, elemanları A matrisinin k satırları ile k satırlarının kesişiminde bulunan determinanttır.

A matrisinin tüm k dereceli minörleri = 0 ise, k + 1 dereceli herhangi bir minör de 0'a eşittir.

Temel minör.

Bir matris A'nın rankı, onun temel minörünün mertebesidir.

Küçükleri sınırlama yöntemi: - A matrisinin sıfır olmayan bir öğesini seçiyoruz (Böyle bir öğe yoksa, A \u003d 0) sırası

1. derecenin bir önceki minörünü 2. derecenin minör ile sınırlıyoruz. (Eğer bu minör 0'a eşit değilse, rank >=2) Eğer bu minörün rankı =0 ise, seçilen 1. dereceden minörü diğer 2. dereceden minörlerle sınırlarız. (2. dereceden tüm küçükler = 0 ise, matrisin sırası = 1).

Matris sıralaması. Bir matrisin rankını bulma yöntemleri.

Bir matris A'nın rankı, onun temel minörünün mertebesidir.

Hesaplama yöntemleri:

1) Küçükleri sınırla yöntemi: -A matrisinin sıfır olmayan bir öğesini seçin (eğer böyle bir öğe yoksa, o zaman 0 sırala) - Önceki 1. dereceden küçük olanı 2. derece küçük ile sınırlayın..gif" width="40 " yükseklik="22" >r+1 Bay+1=0.

2) Bir matrisi basamaklı bir forma getirmek: bu yöntem, temel dönüşümlere dayanmaktadır. Temel dönüşümler altında matrisin sırası değişmez.

Aşağıdaki dönüşümlere temel dönüşümler denir:

İki satırın (sütunların) permütasyonu.

Bir sütunun (satırın) tüm elemanlarının =0 olmayan bir sayı ile çarpımı.

Belirli bir sütunun (satırın) tüm öğelerine, daha önce aynı sayı ile çarpılmış başka bir sütunun (satırın) öğelerinin eklenmesi.

Temel minör teoremi. Determinantın sıfıra eşit olması için gerekli ve yeterli koşul.

A matrisinin temel minörü, 0'dan farklı olan en büyük k'inci mertebenin minörüdür.

Temel minör teoremi:

Temel satırlar (sütunlar) doğrusal olarak bağımsızdır. A matrisinin herhangi bir satırı (sütun), temel satırların (sütunların) doğrusal bir birleşimidir.

Notlar: Kesişmelerinde temel bir minör bulunan satır ve sütunlara sırasıyla temel satırlar ve sütunlar denir.

a11 a12… a1r a1j

a21 a22….a2r a2j

a31 a32….a3r a3j

ar1 ar2 ….arr arj

ak1 ak2…..akr akj

Determinantın sıfıra eşit olması için gerekli ve yeterli koşullar:

n. mertebenin determinantının = 0 olması için satırlarının (sütunlarının) lineer bağımlı olması gerekli ve yeterlidir.

Lineer denklem sistemleri, sınıflandırılması ve gösterim biçimleri. Cramer kuralı.

Üç bilinmeyenli 3 lineer denklem sistemi düşünün:

https://pandia.ru/text/78/365/images/image020_29.gif" alt="(!LANG:l14image048" width="64" height="38 id=">!}

sistemin determinantı denir.

Aşağıdaki gibi üç determinant daha oluşturuyoruz: D determinantında art arda 1, 2 ve 3 sütunu bir serbest terimler sütunu ile değiştiriyoruz

https://pandia.ru/text/78/365/images/image022_23.gif" alt="(!LANG:l14image052" width="93" height="22 id=">!}

Kanıt. Bu nedenle, üç bilinmeyenli 3 denklemli bir sistem düşünün. Sistemin 1. denklemini a11 öğesinin cebirsel tümleyeni A11, 2. denklemi A21 ve 3. denklemi A31 ile çarpıyoruz:

https://pandia.ru/text/78/365/images/image024_24.gif" alt="(!LANG:l14image056" width="247" height="31 id=">!}

Parantezlerin her birini ve bu denklemin sağ tarafını düşünün. 1. sütunun elemanları açısından determinantın genişlemesi üzerine teorem ile

https://pandia.ru/text/78/365/images/image026_23.gif" alt="(!LANG:l14image060)" width="324" height="42 id=">!}

Benzer şekilde, ve gösterilebilir.

Son olarak, bunu görmek kolaydır

Böylece eşitliği elde ederiz: .

Buradan, .

Eşitlikler ve benzer şekilde türetilir, buradan teoremin iddiası gelir.

Lineer denklem sistemleri. Doğrusal denklemler için uyumluluk koşulu. Kronecker-Capelli teoremi.

Bir cebirsel denklem sisteminin çözümü, x1,x2,x3…..xn yerine orijinal sisteme değiştirildiğinde, C1,C2,C3……Cn gibi bir n sayı kümesidir, tüm denklemleri döndürür. sistem kimliklere dönüştürülür.

Bir lineer cebirsel denklem sistemi, en az bir çözümü varsa tutarlı olarak adlandırılır.

Ortak bir sisteme, tek bir çözümü varsa kesin, sonsuz sayıda çözümü varsa belirsiz denir.

Lineer cebirsel denklem sistemlerinin uyumluluğu için koşullar.

a11 a12 ……a1n x1 b1

a21 a22 ……a2n x2 b2

……………….. .. = ..

am1 am2…..amn xn bn

TEOREM: n bilinmeyenli m lineer denklem sisteminin tutarlı olması için, genişletilmiş matrisin rankının A matrisinin rankına eşit olması gerekli ve yeterlidir.

Not: Bu teorem yalnızca bir çözümün varlığı için ölçütler verir, ancak bir çözüm bulmanın bir yolunu göstermez.

10 soru.

Lineer denklem sistemleri. Temel minör yöntemi, lineer denklem sistemlerinin tüm çözümlerini bulmak için genel bir yöntemdir.

A=a21 a22…..a2n

Temel minör yöntemi:

Sistemin uyumlu ve RgA=RgA'=r olmasına izin verin. Temel minör A matrisinin sol üst köşesine boyansın.

https://pandia.ru/text/78/365/images/image035_20.gif" width="22" height="23 src=">…...gif" width="23" height="23 src= ">…...gif" width="22" height="23 src=">…...gif" width="46" height="23 src=">-…..-a

d2 b2-a(2r+1)x(r+1)-..-a(2n)x(n)

… = …………..

Dr br-a(rr+1)x(r+1)-..-a(rn)x(n)

https://pandia.ru/text/78/365/images/image050_12.gif" width="33" height="22 src=">

Açıklamalar: Ana matrisin rankı ve dikkate alınan r=n'ye eşitse, bu durumda dj=bj ve sistemin benzersiz bir çözümü vardır.

Lineer denklemlerin homojen sistemleri.

Tüm serbest terimleri sıfıra eşitse, bir lineer cebirsel denklem sistemine homojen denir.

AX=0 homojen bir sistemdir.

AX = B homojen olmayan bir sistemdir.

Homojen sistemler her zaman tutarlıdır.

X1 =x2 =..=xn =0

Teorem 1.

Homojen sistemler, sistem matrisinin rankı bilinmeyen sayısından az olduğunda homojen olmayan çözümlere sahiptir.

Teorem 2.

A matrisinin determinantı sıfıra eşit olduğunda, n bilinmeyenli homojen bir n-lineer denklem sistemi sıfır olmayan bir çözüme sahiptir. (detA=0)

Homojen sistemlerin çözümlerinin özellikleri.

Homojen bir sistem için bir çözümün herhangi bir lineer kombinasyonu, bu sistemin kendisi için bir çözümdür.

a1C1 +a2C2; α1 ve α2 bazı sayılardır.

A(α1C1 + α2C2) = A(α1C1) + A(α2C2) = α1(A C1) + α2(AC2) = 0, yani. k.(A C1) = 0; (AC2) = 0

Homojen olmayan bir sistem için bu özellik geçerli değildir.

Temel karar sistemi.

Teorem 3.

n bilinmeyenli bir denklemin matris sisteminin rankı r ise, bu sistemin n-r lineer bağımsız çözümü vardır.

Temel minör sol üst köşede olsun. eğer r< n, то неизвестные х r+1;хr+2;..хn называются свободными переменными, а систему уравнений АХ=В запишем, как Аr Хr =Вr

C1 = (C11 C21 .. Cr1 , 1.0..0)

C2 = (C21 C22 .. C2r,0, 1..0)<= Линейно-независимы.

……………………..

Cn-r = (Cn-r1 Cn-r2 .. Cn-rr ,0, 0..1)

Sıra r'nin n-bilinmeyenlerine sahip homojen bir lineer denklem sisteminin n-r lineer bağımsız çözümlerinden oluşan bir sisteme temel çözümler sistemi denir.

Teorem 4.

Bir lineer denklem sisteminin herhangi bir çözümü, temel sistemin bir çözümünün lineer bir birleşimidir.

С = α1C1 + α2C2 + .. + αn-r Cn-r

eğer r

12 soru.

Homojen olmayan bir sistemin genel çözümü.

Uyku (gen. tek tip olmayan) \u003d COO + SCH (özel)

AX=B (heterojen sistem); AX=0

(ASoo) + ASch = ASch = B, çünkü (ASoo) = 0

Uyku \u003d α1C1 + α2C2 + .. + αn-r Cn-r + Orta

Gauss yöntemi.

Bu, bilinmeyenlerin (değişkenlerin) art arda ortadan kaldırılması için bir yöntemdir - temel dönüşümlerin yardımıyla, orijinal denklem sisteminin, diğer tüm değişkenlerin sırayla bulunduğu kademeli bir formun eşdeğer bir sistemine indirgenmesi gerçeğinden oluşur. , son değişkenlerden başlayarak.

a≠0 olsun (eğer durum böyle değilse, o zaman bu denklemler yeniden düzenlenerek elde edilir).

1) x1 değişkenini ikinci, üçüncü ... n-inci denklemden çıkarırız, ilk denklemi uygun sayılarla çarparız ve elde edilen sonuçları 2., 3. ... n-inci denkleme ekleriz, sonra şunu elde ederiz:

Orijinaline eşdeğer bir sistem elde ediyoruz.

2) x2 değişkenini hariç tut

3) x3 vb. değişkeni hariç tutuyoruz.

x4;x5...xr-1 değişkenlerinin sıralı eleme sürecine devam ederek (r-1)-inci adım için elde ederiz.

Denklemlerdeki son n-r'nin sıfır sayısı, sol taraflarının şöyle göründüğü anlamına gelir: 0x1 +0x2+..+0xn

вr+1, вr+2… sayılarından en az biri sıfıra eşit değilse, karşılık gelen eşitlik tutarsızdır ve sistem (1) tutarlı değildir. Böylece, herhangi bir tutarlı sistem için bu vr+1 … vm sıfıra eşittir.

Sistemdeki son n-r denklemleri (1;r-1) özdeştir ve göz ardı edilebilir.

İki durum mümkündür:

a) sistemin denklem sayısı (1; r-1) bilinmeyenlerin sayısına eşittir, yani. r \u003d n (bu durumda, sistem üçgen bir şekle sahiptir).

b)r

Sistem (1)'den eşdeğer bir sisteme (1; r-1) geçişe Gauss yönteminin doğrudan hareketi denir.

Sistemden bir değişken bulma hakkında (1; r-1) - Gauss yönteminin tersi yönünde.

Gauss dönüşümleri, bunları denklemlerle değil, katsayılarının genişletilmiş bir matrisiyle uygulayarak rahatlıkla gerçekleştirilir.

13 soru.

benzer matrisler.

Yalnızca n/ mertebesindeki kare matrisleri dikkate alacağız.

A=S-1BS olacak şekilde tekil olmayan bir S matrisi varsa, A matrisinin B (A~B) matrisine benzer olduğu söylenir.

Benzer matrislerin özellikleri.

1) Matris A kendisine benzer. (A~A)

S=E ise, EAE=E-1AE=A

2) A~B ise, B~A

A=S-1BS => SAS-1= (SS-1)B(SS-1)=B ise

3) Eğer A~B ve aynı zamanda B~C ise, o zaman A~C

A=S1-1BS1 ve B=S2-1CS2 => A= (S1-1 S2-1) C(S2 S1) = (S2 S1)-1C(S2 S1) = S3-1CS3 olduğu göz önüne alındığında, burada S3 = S2S1

4) Benzer matrislerin determinantları eşittir.

A~B verildiğinde, detA=detB olduğunu kanıtlamak gerekir.

A=S-1 BS, detA=det(S-1 BS)= detS-1* detB* detS = 1/detS *detB*detS (azalt) = detB.

5) Benzer matrislerin rankları aynıdır.

Matrislerin özvektörleri ve özdeğerleri.

AX = λ X olacak şekilde sıfır olmayan bir X vektörü (matris sütunu) varsa, X vektörüne A matrisinin özvektörü denir ve tüm özdeğerler kümesine A matrisinin özdeğeri denir. A matrisinin spektrumu denir.

Özvektörlerin özellikleri.

1) Bir özvektörü bir sayı ile çarparken, aynı özdeğere sahip bir özvektör elde ederiz.

AX \u003d λ X; Х≠0

α X => A (α X) \u003d α (AX) \u003d α (λ X) \u003d \u003d λ (α X)

2) İkili olarak farklı özdeğerleri olan özvektörler lineer olarak bağımsız λ1, λ2,.. λk.

Sistem 1. vektörden oluşsun, endüktif bir adım atalım:

C1 X1 + C2 X2 + .. + Cn Xn = 0 (1) - A ile çarpın.

C1 AX1 + C2 AX2 + .. + Cn AXn \u003d 0

С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn = 0

λn+1 ile çarp ve çıkar

C1 X1 +C2 X2 + .. +Cn Xn+ Cn+1 Xn+1 = 0

С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn+ Сn+1 λn+1 Хn+1 = 0

C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn + Cn+1 (λn+1 –λn+1)Xn+1 = 0

C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn = 0

C1 \u003d C2 \u003d ... \u003d Cn \u003d 0 olması gerekir

Cn+1 Xn+1 λn+1 =0

Karakteristik denklem.

A-λE, A matrisi için karakteristik matris olarak adlandırılır.

Sıfır olmayan bir X vektörünün, λ özdeğerine karşılık gelen A matrisinin bir özvektörü olması için, homojen bir lineer cebirsel denklem sisteminin (A - λE)X = 0 çözümü olması gerekir.

det (A - XE) = 0 olduğunda sistemin önemsiz bir çözümü vardır - bu karakteristik bir denklemdir.

İfade!

Benzer matrislerin karakteristik denklemleri çakışır.

det(S-1AS - λЕ) = det(S-1AS - λ S-1ЕS) = det(S-1 (A - λЕ)S) = det S-1 det(A - λЕ) detS= det(A - λЕ)

Karakteristik polinom.

det(A – λЕ) - λ parametresine göre fonksiyon

det(A – λЕ) = (-1)n Xn +(-1)n-1(a11+a22+..+ann)λn-1+..+detA

Bu polinom, A matrisinin karakteristik polinomu olarak adlandırılır.

Sonuç:

1) Matrisler A~B ise, köşegen elemanlarının toplamı aynıdır.

a11+a22+..+ann = в11+в22+..+вnn

2) Benzer matrislerin özdeğerleri kümesi çakışır.

Matrislerin karakteristik denklemleri aynıysa, mutlaka benzer olmaları gerekmez.

A matrisi için

B matrisi için

https://pandia.ru/text/78/365/images/image062_10.gif" width="92" height="38">

Det(Ag-λE) = (λ11 – λ)(λ22 – λ)…(λnn – λ)= 0

A matrisinin n mertebesinde köşegenleştirilebilmesi için, A matrisinin lineer bağımsız özvektörlerinin olması gerekir.

Sonuç.

A matrisinin tüm özdeğerleri farklıysa, köşegenleştirilebilir.

Özvektörleri ve özdeğerleri bulmak için algoritma.

1) karakteristik denklemi oluşturun

2) denklemlerin köklerini bulun

3) özvektörü belirlemek için bir denklem sistemi oluşturur.

λi (A-λi E)X = 0

4) temel çözüm sistemini bulun

x1,x2..xn-r, burada r, karakteristik matrisin rankıdır.

r = Rg(A - λi E)

5) özvektör, özdeğerler λi şu şekilde yazılır:

X \u003d C1 X1 + C2 X2 + .. + Cn-r Xn-r, burada C12 + C22 + ... C2n ≠0

6) matrisin köşegen bir forma indirgenip indirgenemeyeceğini kontrol ederiz.

7) Ag'yi bul

Ag = S-1AS S=

15 soru.

Doğru, düzlem, uzayın temeli.

https://pandia.ru/text/78/365/images/image065_9.gif" height="11">│, ││). Bu vektör sıfır olduğunda vektör modülü sıfırdır (│ō│=0)

4.Ort vektörü.

Belirli bir vektörün ort'u, verilen vektörle aynı yöne ve bire eşit bir modüle sahip bir vektördür.

Eşit vektörlerin eşit ortları vardır.

5. İki vektör arasındaki açı.

Bu, aynı noktadan çıkan ve verilen vektörlerle aynı yöne yönlendirilen iki ışınla sınırlanan alanın daha küçük kısmıdır.

Vektörlerin eklenmesi. Bir vektörü bir sayı ile çarpma.

1) İki vektörün eklenmesi

https://pandia.ru/text/78/365/images/image065_9.gif" height="11">+ │≤│ │+│ │

2) Bir vektörün bir skaler ile çarpımı.

Bir vektörün ve bir skalerin çarpımı şu özelliklere sahip yeni bir vektördür:

a) = skalerin mutlak değeri ile çarpılan vektörün modülünün ürünleri.

b) skaler pozitifse yön çarpılan vektörle aynı, skaler negatifse terstir.

λ a(vektör)=>│ λ │= │ λ │=│ λ ││ │

Vektörlerde doğrusal işlemlerin özellikleri.

1. İletişimsellik Yasası.

2. Çağrışım yasası.

3. Sıfır ile toplama.

a(vektör)+o= a(vektör)

4. Zıttı ile toplama.

5. (αβ) = α(β) = β(α)

6;7 Dağılım yasası.

Bir vektörün modülü ve birim vektörü cinsinden ifadesi.

Lineer bağımsız vektörlerin maksimum sayısına baz denir.

Bir çizgi üzerindeki taban, sıfır olmayan herhangi bir vektördür.

Düzlemdeki bir temel, çağrılmayan herhangi iki vektördür.

Uzayda bir taban, aynı düzlemde olmayan herhangi üç vektörden oluşan bir sistemdir.

Bir vektörün bazı bazlardaki genişleme katsayısına, vektörün verilen bazdaki bileşenleri veya koordinatları denir.

https://pandia.ru/text/78/365/images/image075_10.gif" height="11 src=">.gif" height="11 src="> toplama ve çarpma işlemini bir skalerle, ardından elde ettiğimiz herhangi bir sayıda eylemle sonuçlanır:

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src=">, bunların ō'ye eşit önemsiz olmayan bir doğrusal kombinasyonu varsa, doğrusal bağımlı olarak adlandırılır.

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src=">, bunların önemsiz olmayan bir doğrusal kombinasyonu yoksa, doğrusal olarak bağımsız olarak adlandırılır.

Lineer bağımlı ve bağımsız vektörlerin özellikleri:

1) sıfır vektörü içeren vektörler sistemi lineer bağımlıdır.

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> lineer bağımlıdır, bazı vektörler diğer vektörlerin lineer bir kombinasyonu olmalıdır.

3) a1 (vektör), a2 (vektör) ... ak (vektör) sisteminden bazı vektörler lineer bağımlıysa, tüm vektörler lineer bağımlıdır.

4)tüm vektörler https://pandia.ru/text/78/365/images/image076_9.gif" height="11 src=">.gif" width="75" height="11"> ise

https://pandia.ru/text/78/365/images/image082_10.gif" height="11 src=">.gif" height="11 src=">)

Koordinatlarda doğrusal işlemler.

https://pandia.ru/text/78/365/images/image069_9.gif" height="12 src=">.gif" height="11 src=">.gif" height="11 src="> .gif" yükseklik="11 kaynak=">.gif" genişlik="65" yükseklik="13 kaynak=">

Nokta ürün özellikleri:

1. Değişebilirlik

3. (a;b)=0 ancak ve ancak vektörler dikse veya vektörlerden herhangi biri 0'a eşitse.

4. Dağılabilirlik (αa+βb;c)=α(a;c)+β(b;c)

5. a ve b'nin skaler çarpımının koordinatları cinsinden ifadesi

https://pandia.ru/text/78/365/images/image093_8.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image095_8.gif" width="254" height="13 src=">

() koşulu olduğunda, h, l=1,2,3

https://pandia.ru/text/78/365/images/image098_7.gif" width="176" height="21 src=">

https://pandia.ru/text/78/365/images/image065_9.gif" height="11"> ve aşağıdaki denklemleri sağlayan üçüncü vektör denir:

3. - sağ

Vektör ürün özellikleri:

4. Koordinat vektörlerinin vektör çarpımı

ortonormal taban.

https://pandia.ru/text/78/365/images/image109_7.gif" width="41" height="11 src=">

https://pandia.ru/text/78/365/images/image111_8.gif" width="41" height="11 src=">

Bir ortonormal bazın ortlarını belirtmek için genellikle 3 sembol kullanılır.

https://pandia.ru/text/78/365/images/image063_10.gif" width="77" height="11 src=">

https://pandia.ru/text/78/365/images/image114_5.gif" width="549" height="32 src=">

Bir ortonormal taban ise, o zaman

https://pandia.ru/text/78/365/images/image117_5.gif" width="116" height="15">- doğrudan paralel eksen OX denklemi

2) - OS eksenine paralel düz bir çizginin denklemi

2. 2 düz çizginin karşılıklı düzenlenmesi.

Teorem 1 Doğruların denklemleri afin koordinat sistemine göre verilsin

A) O zaman kesiştikleri zaman gerekli ve yeterli koşul:

B) O halde doğruların paralel olması için gerekli ve yeterli koşul şudur:

B) O halde doğruların birleşmesi için gerekli ve yeterli koşul şudur:

3. Bir noktadan bir çizgiye olan mesafe.

Teorem. Kartezyen koordinat sistemine göre bir noktadan bir çizgiye olan mesafe:

https://pandia.ru/text/78/365/images/image127_7.gif" width="34" height="11 src=">

4. İki düz çizgi arasındaki açı. Dikey durum.

Genel denklemlerle Kartezyen koordinat sistemine göre 2 doğru verilsin.

https://pandia.ru/text/78/365/images/image133_4.gif" width="103" height="11 src=">

Eğer , o zaman çizgiler diktir.

24 soru.

uzayda uçak. Bir vektör ve bir düzlem için benzerlik koşulu. Bir noktadan bir düzleme olan mesafe. İki düzlemin paralellik ve diklik durumu.

1. Bir vektör ve bir düzlem için benzerlik koşulu.

https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image140.jpg" alt="(!LANG:Untitled4.jpg" width="111" height="39">!}

https://pandia.ru/text/78/365/images/image142_6.gif" width="86" height="11 src=">

https://pandia.ru/text/78/365/images/image144_6.gif" width="148" height="11 src=">

https://pandia.ru/text/78/365/images/image145.jpg" alt="(!LANG:Untitled5.jpg" width="88" height="57">!}

https://pandia.ru/text/78/365/images/image147_6.gif" width="31" height="11 src=">

https://pandia.ru/text/78/365/images/image148_4.gif" width="328" height="24 src=">

3. 2 düzlem arasındaki açı. Dikey durum.

https://pandia.ru/text/78/365/images/image150_6.gif" width="132" height="11 src=">

Eğer , o zaman düzlemler diktir.

25 soru.

Uzayda düz çizgi. Uzayda düz bir çizginin çeşitli denklem türleri.

https://pandia.ru/text/78/365/images/image156_6.gif" width="111" height="19">

2. Uzayda düz bir çizginin vektör denklemi.

https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image162_5.gif" width="44" height="29 src=">

4. Kanonik denklem doğrudandır.

https://pandia.ru/text/78/365/images/image164_4.gif" width="34" height="18 src=">

https://pandia.ru/text/78/365/images/image166_0.jpg" alt="(!LANG:Untitled3.jpg" width="56" height="51">!}

Lineer cebir problemleri. Bir matris kavramı. Matris türleri. Matrislerle işlemler. Matrislerin dönüşümü ile ilgili problemlerin çözümü.

Matematiğin çeşitli problemlerini çözerken, genellikle matris adı verilen sayı tablolarıyla uğraşmak gerekir. Matrislerin yardımıyla, doğrusal denklem sistemlerini çözmek, vektörlerle birçok işlemi gerçekleştirmek, çeşitli bilgisayar grafikleri problemlerini ve diğer mühendislik görevlerini çözmek uygundur.

matris denir bir sayı içeren dikdörtgen bir sayı tablosu mçizgiler ve bazı P sütunlar. sayılar t ve P matris siparişleri denir. Eğer t = P, matrise kare denir ve sayı m = n- onun siparişi.

Aşağıda, matris yazmak için çift tire veya parantez kullanılacaktır:

Veya

Kısa bir matris ataması için, tek bir büyük Latin harfi (örneğin, A) veya sembolü sıklıkla kullanılacaktır. || bir ij || ve bazen bir açıklama ile: ANCAK = || bir ij || = (aij), nerede (i = 1, 2, ..., m, j=1, 2, ..., n).

sayılar aij , Bu matrisin parçası olan öğelere öğeleri denir. kayıtta aij ilk indeks і satır numarası ve ikinci dizin anlamına gelir j- sütun numarası. Bir kare matris durumunda

(1.1)

ana ve ikincil köşegen kavramları tanıtılır. Matrisin (1.1) ana köşegeni köşegendir. bir 11 bir 12 … ann bu matrisin sol üst köşesinden sağ alt köşesine gidiyor. Aynı matrisin yan köşegenine köşegen denir. bir n 1 bir (n -1) 2… 1 n , sol alt köşeden sağ üst köşeye gidiyor.

Matrislerle ilgili temel işlemler ve özellikleri.

Matrislerde temel işlemlerin tanımına geçelim.

Matris ekleme. iki matrisin toplamı Bir = || bir ij || , nerede ve B = || b ij || , nerede (i = 1, 2, ..., m, j=1, 2, ..., n) aynı emirler t ve P matris denir C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., n) aynı emirler t ve P, elementler ij ile formül ile belirlenir

, nerede (i = 1, 2, ..., m, j=1, 2, ..., n)(1.2)

İki matrisin toplamını belirtmek için notasyonu kullanırız. C \u003d A + B. Matrislerin toplamını oluşturma işlemine toplama denir. Yani, tanım gereği:

+ =

Matrislerin toplamının tanımından veya daha doğrusu formüllerden (1.2), doğrudan matris toplama işleminin, gerçek sayıların toplanması işlemiyle aynı özelliklere sahip olduğu, yani:

1) değişmeli özellik: A + B = B + A,

2) kombinasyon özelliği: ( A + B) + C = A + (B + C).

Bu özellikler, iki veya daha fazla matris eklerken matris terimlerinin sırasını önemsememeyi mümkün kılar.

Bir matrisi bir sayı ile çarpmak. A matrisinin çarpımı = || bir ij || , burada (i = 1, 2, ..., m, j=1, 2, ..., n) l gerçek sayısı ile matris denir C = || c ij || (i=1,2, ..., m; j = 1, 2, ...., n), unsurları aşağıdaki formülle belirlenir:

, nerede (i = 1, 2, ..., m, j=1, 2, ..., n)(1.3)

Bir matrisin çarpımını bir sayı ile belirtmek için notasyon kullanılır. C \u003d l A veya C \u003d A l. Bir matrisin çarpımını bir sayı ile toplama işlemine, bir matrisin bu sayı ile çarpılması işlemine denir.

Formül (1.3)'ten, bir matrisin bir sayı ile çarpımının aşağıdaki özelliklere sahip olduğu açıktır:

1) sayısal bir faktöre göre bir ilişkisel özellik: (l m) A = l (m A);

2) matrislerin toplamına göre dağılım özelliği: l (A + B) = lA + lB;

3) sayıların toplamına göre dağılma özelliği: (l + m) A = l A + m A

Yorum. iki matrisin farkı ANCAK ve AT aynı siparişler t ve P böyle bir matris aramak doğaldır İle aynı emirler t ve P, matris ile toplamda B A matrisini verir. Doğal gösterim, iki matrisin farkını belirtmek için kullanılır: C \u003d A - B.

Farkı doğrulamak çok kolay İle iki matris ANCAK ve AT kurala göre alınabilir C \u003d A + (-1) B.

matrislerin çarpımı veya matris çarpımı.

matris ürün Bir = || bir ij || , burada (i = 1, 2, ..., m, j = 1, 2, ..., n) sırasıyla eşit emirlere sahip olmak t ve n, matrise B = || b ij || , nerede (i = 1, 2, ..., n , j=1, 2, ..., p), sırasıyla eşit emirlere sahip olmak n ve R, matris denir C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., p) sırasıyla eşit siparişleri olan t ve R unsurları aşağıdaki formülle belirlenir:

nerede (i = 1, 2, ..., m, j = 1, 2, ..., p)(1.4)

Bir matrisin ürününü belirtmek için ANCAK matrise AT kaydı kullan C = A × B. Matris ürün çalışması ANCAK matrise AT bu matrislerin çarpımı denir.

Yukarıdaki tanımdan, A matrisi herhangi bir B matrisi ile çarpılamaz, matrisin sütun sayısının olması gerekir. ANCAK matris satırlarının sayısına eşitti AT.

Formül (1.4), matrisin ürünü olan C matrisinin elemanlarını derlemek için bir kuraldır. ANCAK matrise AT. Bu kural sözlü olarak da formüle edilebilir: C = A B matrisinin i-inci satırının ve j-inci sütununun kesişiminde bulunan ci i j elemanı, A matrisinin i-inci satırının karşılık gelen elemanlarının ikili ürünlerinin toplamına eşittir ve B matrisinin j-inci sütunu.

Bu kuralın uygulanmasına bir örnek olarak, ikinci dereceden kare matrisleri çarpma formülünü sunuyoruz.

× =

Formül (1.4), matris ürününün aşağıdaki özelliklerini ifade eder ANCAK matris üzerinde AT:

1) birleştirici özellik: (A B) C = A (B C);

2) matrislerin toplamına göre dağılım özelliği:

(A + B) C = A C + B C veya A (B + C) = A B + A C.

Bir matrisin ürününün permütasyon (değişmeli) özelliği sorusu A matrise AT sadece kare matrisler için ayarlamak mantıklıdır A ve B aynı sipariş.

Permütasyon özelliğinin de geçerli olduğu matrislerin önemli özel durumlarını sunuyoruz. Permütasyon özelliğinin geçerli olduğu çarpım için iki matrise genellikle değişme denir.

Kare matrisler arasında, her biri ana köşegenin dışında sıfıra eşit elemanlara sahip olan köşegen matrisler sınıfını seçiyoruz. Her köşegen düzen matrisi P forma sahip

D= (1.5)

nerede d1, d2,… ,dn-herhangi bir numara. Tüm bu sayıların birbirine eşit olup olmadığını görmek kolaydır, yani. d1=d2=… = dn sonra herhangi bir kare matris için ANCAK sipariş P adil eşitlik A D = D A.

Çakışan girişleri olan tüm çapraz matrisler (1.5) arasında d1=d2=… = gün = = d iki matris özellikle önemli bir rol oynar. Bu matrislerin ilki şu şekilde elde edilir: d=1 kimlik matrisi denir n E.İkinci matris ile elde edilir d=0, boş matris olarak adlandırılır n inci sıra ve sembolü ile gösterilir ey Böylece,

E= O=

Yukarıda kanıtlananlar sayesinde A E = E A ve A O = O A.Üstelik bunu göstermek kolaydır.

A E \u003d E A \u003d A, A O \u003d O A \u003d 0. (1.6)

Formüllerin (1.6) ilki, kimlik matrisinin özel rolünü karakterize eder. E, gerçek sayıların çarpımında 1 sayısının oynadığı role benzer. Sıfır matrisinin özel rolüne gelince Ö, o zaman sadece formüllerin (1.7) ikincisiyle değil, aynı zamanda temel olarak doğrulanabilir eşitlikle de ortaya çıkar.

A + 0 = 0 + A = A.

Sonuç olarak, sıfır matris kavramının kare olmayan matrisler için de sunulabileceğini not ediyoruz (sıfır denir. hiç tüm elemanları sıfıra eşit olan matris).

Blok matrisler

Bazı matris varsayalım Bir = || bir ij || yatay ve dikey çizgiler kullanılarak, her biri daha küçük boyutlu bir matris olan ve orijinal matrisin bloğu olarak adlandırılan ayrı dikdörtgen hücrelere bölünür. Bu durumda, orijinal matrisi düşünmek mümkün hale gelir. ANCAK bazı yeni (sözde blok) matris olarak ANCAK = || bir b ||, öğeleri belirtilen bloklardır. Bu öğeleri, genel olarak, sayı değil matrisler olduklarını vurgulamak için büyük bir Latin harfiyle belirtiriz ve (sıradan sayısal öğeler gibi) iki dizin sağlarız, bunlardan ilki "blok" satırının numarasını gösterir ve ikincisi - "blok" satırının numarası. » sütun.

Örneğin, matris

bir blok matris olarak görülebilir

öğeleri aşağıdaki bloklardır:

Blok matrislerle yapılan temel işlemlerin, sıradan sayısal matrislerle gerçekleştirildikleri aynı kurallara göre gerçekleştirilmesi, yalnızca blokların eleman olarak hareket etmesi gerçeğidir.

Belirleyici kavramı.

Herhangi bir sıranın keyfi bir kare matrisini düşünün P:

bir= (1.7)

Bu tür her bir matrisle, bu matrise karşılık gelen determinant adı verilen iyi tanımlanmış bir sayısal karakteristik ilişkilendiririz.

eğer sipariş n matris (1.7) bire eşitse, bu matris bir elemandan oluşur bir ben j böyle bir matrise karşılık gelen birinci dereceden determinanttır, bu elemanın değerini arayacağız.

o zaman böyle bir matrise karşılık gelen ikinci dereceden determinant, sayıya eşittir a 11 a 22 - a 12 a 21 ve sembollerden biri ile gösterilir:

Yani tanım gereği

(1.9)

Formül (1.9), kendisine karşılık gelen matrisin elemanlarından ikinci dereceden bir determinantın derlenmesi için bir kuraldır. Bu kuralın sözlü formülasyonu şu şekildedir: matris (1.8)'e karşılık gelen ikinci dereceden determinant, bu matrisin ana köşegenindeki elemanların çarpımı ile ikincil köşegenindeki elemanların çarpımı arasındaki farka eşittir. İkinci ve daha yüksek mertebeden determinantlar, lineer denklem sistemlerinin çözümünde yaygın olarak kullanılmaktadır.

nasıl çalıştığını görelim MathCad sisteminde matrislerle işlemler . En basit matris cebir işlemleri, MathCad'de operatörler olarak uygulanmaktadır. Operatörleri anlam açısından yazmak, matematiksel eylemlerine mümkün olduğunca yakındır. Her operatör, karşılık gelen bir sembolle ifade edilir. MathCad 2001'in matris ve vektör işlemlerini düşünün. Vektörler, boyut matrislerinin özel bir halidir. n x 1, bu nedenle, kısıtlamalar özellikle belirtilmedikçe (örneğin, bazı işlemler yalnızca kare matrisler için geçerlidir) matrisler için olduğu gibi aynı işlemlerin tümü onlar için geçerlidir. nxn). Bazı eylemler yalnızca vektörler için geçerlidir (örneğin, skaler çarpım) ve bazıları aynı yazımlara rağmen vektörler ve matrisler üzerinde farklı davranır.

q OK düğmesine bastıktan sonra, matris öğelerini girmek için bir alan açılır. Bir matris elemanı girmek için imleci işaretli konuma getirin ve klavyeden bir sayı veya ifade girin.

Araç çubuğunu kullanarak herhangi bir işlemi gerçekleştirmek için yapmanız gerekenler:

q matrisi seçin ve paneldeki işlem düğmesine tıklayın,

q veya paneldeki düğmesine tıklayın ve işaretli konuma matrisin adını girin.

“Semboller” menüsü üç işlem içerir - devrik, ters çevir, determinant.

Bu, örneğin komutu yürüterek matris determinantını hesaplayabileceğiniz anlamına gelir. Semboller/Matrisler/Determinant.

MathCAD matrisinin ilk satırının (ve ilk sütununun) numarası ORIGIN değişkeninde saklanır. Varsayılan olarak, geri sayım sıfırdandır. Matematiksel gösterimde, 1'den saymak daha yaygındır. MathCAD'in satır ve sütun numaralarını 1'den sayabilmesi için, ORIGIN:=1 değişkenini ayarlamanız gerekir.

Lineer cebir problemleriyle çalışmaya yönelik fonksiyonlar, “Insert Function” diyalog kutusunun “Vektörler ve Matrisler” bölümünde toplanır (“Standart” panelindeki buton ile çağrıldığını hatırlatırız). Bu işlevlerin başlıcaları daha sonra açıklanacaktır.

aktarma

Benzer bilgiler.