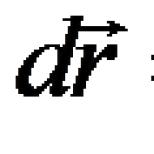Vektörlerin lineer bağımsızlığının durumu. Lineer uzay vektörlerinin lineer bağımlılığı ve bağımsızlığı. Üç boyutlu uzay vektörlerinin lineer bağımlılığı ve bağımsızlığı. Mekansal temel ve afin koordinat sistemi

Tanım 18.2 fonksiyon sistemif, ..., fpismindebenense o h boşlukta a in ve c ve m. o d(a, (3) biraz önemsiz ise 5 bu fonksiyonların lineer kombinasyonu bu aralıkta aynı şekilde sıfıra eşittir:

Tanım 18.3 vektör sistemi f 1 , ..., x n, a ve c'de doğrusal olarak adlandırılır ve bu vektörlerin önemsiz olmayan, doğrusal bir kombinasyonu madde işareti vektörüne eşitse, m o d:

L Karışıklığı önlemek için, vektör bileşeninin (vektör-fonksiyonu) sayısını alt indeksle ve vektörün kendisinin sayısını (eğer böyle birkaç vektör varsa) üst indeksle göstereceğiz.

"Size, içindeki tüm katsayılar sıfır değilse, doğrusal bir kombinasyonun önemsiz olarak adlandırıldığını hatırlatırız.

Tanım 18.4 x 1 ^),..., x n (t) vektör fonksiyonları sistemine doğrusal denir h ve içinde ve ile ve aralıkta benim yaklaşık th,(a, /3) bu vektör fonksiyonlarının bazı önemsiz doğrusal kombinasyonları bu aralıktaki sıfır vektörüne aynı şekilde eşitse:

Bu üç kavramın (fonksiyonların lineer bağımlılığı, vektörler ve vektör fonksiyonları) birbirleriyle olan bağlantısını anlamak önemlidir.

Her şeyden önce, (18.6) formülünü genişletilmiş biçimde sunarsak (her birinin x g (1) bir vektördür)

o zaman eşitlik sistemine eşdeğer olacaktır

ilk tanım anlamında (fonksiyonlar olarak) rth bileşenlerinin doğrusal bağımlılığı anlamına gelir. Vektör fonksiyonlarının lineer bağımlılığının onların ima ettiği söylenir. bileşen bileşen doğrusal bağımlılık.

Bunun tersi genellikle doğru değildir: bir çift vektör fonksiyonu örneğini ele almak yeterlidir.

Bu vektör fonksiyonlarının ilk bileşenleri basitçe çakışır, bu da onların lineer olarak bağımlı oldukları anlamına gelir. İkinci bileşenler orantılıdır, yani. ayrıca lineer bağımlıdır. Bununla birlikte, sıfıra eşit lineer kombinasyonlarını aynı şekilde oluşturmaya çalışırsak, o zaman ilişkiden

hemen sistemi al

tek çözümü olan C - C-2 - 0. Böylece vektör fonksiyonlarımız lineer bağımsızdır.

Böyle garip bir özelliğin nedeni nedir? Bilerek bağımlı işlevlerden doğrusal olarak bağımsız vektör işlevleri oluşturmanıza izin veren hile nedir?

Bütün noktanın bileşenlerin doğrusal bağımlılığında değil, sıfır elde etmek için gerekli olan katsayıların oranında olduğu ortaya çıktı. Vektör fonksiyonlarının doğrusal bağımlılığı durumunda, aynı katsayı seti, sayıdan bağımsız olarak tüm bileşenlere hizmet eder. Ancak örneğimizde, bir bileşen için bir katsayı oranı ve diğeri için başka bir katsayı gerekliydi. Yani hile aslında basittir: "bileşen-bileşen" doğrusal bağımlılıktan tüm vektör fonksiyonlarının doğrusal bir bağımlılığını elde etmek için, tüm bileşenlerin "aynı oranda" doğrusal olarak bağımlı olması gerekir.

Şimdi vektör fonksiyonlarının lineer bağımlılığı ile vektörler arasındaki ilişkinin çalışmasına dönelim. Burada, vektör fonksiyonlarının lineer bağımlılığının, her sabit için t* vektör

lineer bağımlı olacaktır.

Genel olarak konuşursak, tersi geçerli değildir: vektörlerin her biri için doğrusal bağımlılığından t vektör fonksiyonlarının doğrusal bağımlılığını izlemez. Bunu iki vektör fonksiyonu örneğinde görmek kolaydır.

saat t=1, t=2 ve t=3 vektör çiftleri elde ederiz

sırasıyla. Her vektör çifti orantılıdır (sırasıyla 1,2 ve 3 katsayılarıyla). Herhangi bir sabit için bunu görmek kolaydır. t* vektör çiftimiz katsayı ile orantılı olacak t*.

Sıfıra eşit olan doğrusal bir vektör fonksiyonları kombinasyonu oluşturmaya çalışırsak, o zaman ilk bileşenler bize zaten ilişkiyi verir.

bu ancak mümkünse İle = İle2 = 0. Böylece vektör fonksiyonlarımız lineer bağımsız çıktı. Yine, bu etkinin açıklaması, vektör fonksiyonlarının doğrusal bağımlılığı durumunda, aynı sabitler kümesi Cj'nin tüm değerlere hizmet etmesidir. t, ve örneğimizde her değer için t katsayılar arasında kendi oranını gerektiriyordu.

Fonksiyonların (n-1) limitinin türevleri olsun.

Belirleyiciyi düşünün: (1)

W(x), fonksiyonlar için Wronsky determinantı olarak adlandırılır.

Teorem 1. Eğer fonksiyonlar (a, b) aralığında lineer olarak bağımlıysa, o zaman onların Wronskian W(x) bu aralıkta aynı şekilde sıfıra eşittir.

Kanıt. Teoremin koşuluna göre, bağıntı

, (2) burada hepsi sıfıra eşit değildir. İzin vermek . Sonra

(3). Bu kimliği n-1 kez farklılaştırın ve,

Elde edilen değerlerin yerine Vronsky determinantının yerine konulması,

elde ederiz:

(4).

Wronsky determinantında, son sütun önceki n-1 sütunlarının doğrusal bir birleşimidir ve bu nedenle (a, b) aralığındaki tüm noktalarda sıfırdır.

Teorem 2. Eğer y1,…, yn fonksiyonları, L[y] = 0 denkleminin lineer bağımsız çözümleri ise, tüm katsayıları (a, b) aralığında sürekli ise, o zaman bu çözümlerin Wronskian'ı, denklemin her noktasında sıfır değildir. aralık (a, b).

Kanıt. Tam tersini varsayalım. X0 vardır, burada W(X0)=0. Bir n denklem sistemi oluşturuyoruz

(5).

Açıkçası, sistem (5) sıfırdan farklı bir çözüme sahiptir. (6) olsun.

y1,…, yn çözümlerinin lineer bir kombinasyonunu oluşturalım.

Y(x), L[y] = 0 denkleminin bir çözümüdür. Ayrıca, . Teklik teoremi sayesinde, L[y] = 0 denkleminin sıfır başlangıç ​​koşuluyla çözümü yalnızca sıfır olabilir, yani .

Hepsinin sıfıra eşit olmadığı kimliği elde ederiz, bu da y1,…, yn'nin lineer bağımlı olduğu anlamına gelir, bu da teoremin koşuluyla çelişir. Bu nedenle, W(X0)=0 olduğu bir nokta yoktur.

Teorem 1 ve Teorem 2'ye dayanarak, aşağıdaki iddiayı formüle edebiliriz. L[y] = 0 denkleminin n çözümünün (a, b) aralığında lineer olarak bağımsız olması için, onların Wronskianlarının bu aralığın herhangi bir noktasında kaybolmaması gerekli ve yeterlidir.

Wronskian'ın aşağıdaki bariz özellikleri de kanıtlanmış teoremlerden kaynaklanmaktadır.

1. L[y] = 0 denkleminin n çözümünün Wronskian'ı, tüm pi(x) katsayılarının sürekli olduğu (a, b) aralığında x = x0'ın bir noktasında sıfıra eşitse, o zaman sıfıra eşittir. bu aralığın tüm noktalarında.
2. L[y] = 0 denkleminin n çözümünün Wronskian'ı (a, b) aralığından x = x0'ın bir noktasında sıfır değilse, o zaman bu aralığın tüm noktalarında sıfır değildir.

Dolayısıyla, pi(x) denkleminin katsayılarının sürekli olduğu (a, b) aralığında L[y] = 0 denkleminin n bağımsız çözümünün doğrusallığı için, Wronskianlarının olması gerekli ve yeterlidir. bu aralığın en az bir noktasında sıfırdan farklı.

Doğrusal (vektör) uzaylar.

Tanım: Bir demet L isminde lineer (vektör) uzay , üzerinde iki işlem tanıtılırsa:

1) ek: herhangi biri için x, y Є L toplam ( x + y) Є L,

2) bir sayı ile çarpma: herhangi biri için x Є L ve herhangi bir sayı λ çarpımı

λx Є L,

8 aksiyomu karşılayan:

1) x + y = y + x, nerede x, y Є L;

2) (x + y)+z = x+(y + z), nerede x, y, z Є L;

3) öyle bir sıfır elemanı var ki Ө Ө + x = x, nerede x Є L;

4) herhangi biri için x Є L sadece bir zıt unsur var

(-X)öyle ki x + (-x) \u003d Ө;

5) 1 x = x, nerede x Є L;

6) α(βх) = (αβ)х, nerede x Є L, α ve β sayılardır;

7) α(x + y) = αx + αy, nerede x, y Є L, a - sayı;

8) (α + β) x = αx + βx, nerede x Є L, α ve β sayılardır.

Yorum: Doğrusal (vektör) uzayın elemanlarına denir. vektörler .

Örnekler:

Gerçek sayılar kümesi doğrusal bir uzaydır.

Düzlemdeki ve uzaydaki tüm vektörlerin kümeleri doğrusal bir uzaydır.

Aynı boyuttaki tüm matrislerin kümesi doğrusal bir uzaydır.

Doğrusal bir uzayda verilen bir vektörler sistemi a 1, a 2, a 3, ... bir n Є L.

Tanım: Vektör α 1 a 1 + α 2 a 2 +…+ α n bir n Є L, nerede bir ben(i = 1,…,n) - denilen sayılar doğrusal kombinasyon (LK) a 1, a 2, a 3, ... a n vektörleri.

Tanım: Doğrusal uzay vektör sistemi a 1, a 2, a 3, ... bir n Є L isminde lineer bağımsız (LNZ) lineer kombinasyon ise

α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n bir n =0 ancak ve ancak katsayılar

α 1 =α 2 =α 3 =…=α n =0.

Tanım: vektör sistemi a 1, a 2, a 3, ... bir n Є L isminde lineer bağımlı (LZ) bir dizi sayı varsa α 1, α 2 ,α 3 … α n, hepsi 0'a eşit değil, öyle ki lineer kombinasyon α 1 a 1 + α 2 a 2 +…+ α n bir n = 0.

Örnekler:

iki vektör denir doğrusal aynı doğruya paralellerse veya aynı doğru üzerindeyseler.

1) Düzlemde sıfır olmayan, doğrusal olmayan iki vektör düşünün. köşegen =0 .

Doğrusal kombinasyon sıfıra eşittir, sıfır olmayan bir katsayı vardır, bu nedenle düzlemdeki iki eşdoğrusal vektör doğrusal olarak bağımlıdır.

Teorem 1. Doğrusal bağımlılık için gerekli ve yeterli koşul.

Lineer uzayda bir vektörler sisteminin lineer bağımlı olması için, bu sistemin bazı vektörlerinin diğerlerinin lineer kombinasyonu olması gerekli ve yeterlidir.

Giriş: İhtiyaç ().

Verilen LZ sistemi. Bir vektörün diğerlerinin LC'si olduğunu kanıtlamak gerekir.

a 1, a 2, a 3, ... bir n– Vektörlerin LZ sistemi, yani. α 1, α 2 ,α 3 … α n arasında sıfırdan farklı bir sayı vardır, böylece LC α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n bir n = 0.

katsayısını belirlediğimizi varsayıyoruz. α1 ≠ 0. Son eşitliğin her iki tarafını da α1 ≠ 0:

Bu nedenle şu şekildedir: 1- Diğer vektörlerin LC'si.

İhtiyaç kanıtlanmıştır.

yeterlilik ().

Bir vektör diğerlerinin lineer birleşimi olsun. LZ vektörlerinin sisteminin olduğunu kanıtlamak gerekir.

İzin vermek α n \u003d α 1 a 1 + α 2a 2 + α 3a 3 + ... + α n -1 bir n -1.

α 1 a 1 + α 2 a 2 + α 3 a 3 + ... + α n -1 bir n -1 - 1α n \u003d 0.

Sıfır olmayan bir katsayı olduğundan, vektörler sistemi a 1, a 2, a 3, ... bir n lineer bağımlıdır.

Teorem 2. Boş bir vektör içeren bir sistem lineer olarak bağımlıdır.

Giriş: Boş bir vektör içeren bir vektörler sistemi düşünün. a 1, a 2, a 3, ... bir n,Ө, nerede Ө boş bir vektördür. Aşağıdaki eşitliğin geçerli olduğu açıktır. 0 а 1 + 0 а 2 +0 а 3 +…+ 5 Ө = 0.

5'e eşit sıfır olmayan bir katsayı vardır ve doğrusal kombinasyon 0'a eşittir, dolayısıyla LZ vektörleri sistemi izler.

Teorem 3. Doğrusal olarak bağımlı bir alt sistem içeren bir sistem de doğrusal olarak bağımlı olacaktır.

Giriş: Vektörler sistemini düşünün a 1, a 2, ..., a k, a k+1 ... bir n, nerede bir 1, bir 2, ..., bir k lineer bağımlı bir parçadır. α 1 a 1 + α 2 a 2 + ... + α k bir k \u003d 0. Sıfır dışında bir katsayı var.

Açıkçası, aynı katsayılarla, eşitlik

α 1 a 1 + α 2 a 2 +…+α k a k +…+0 a k+1 +…+ 0 α n = 0.

Dolayısıyla, LZ vektörleri sistemi izler.

Bu yazıda şunları ele alacağız:

• doğrusal vektörler nelerdir;
• doğrusal vektörler için koşullar nelerdir;
• eşdoğrusal vektörlerin özellikleri nelerdir;
• eşdoğrusal vektörlerin doğrusal bağımlılığı nedir.

Doğrusal vektörler, aynı doğruya paralel olan veya aynı doğru üzerinde bulunan vektörlerdir.

örnek 1

Doğrusal vektörler için koşullar

Aşağıdaki koşullardan herhangi biri doğruysa iki vektör eşdoğrusaldır:

• koşul 1 . a = λ b olacak şekilde bir λ sayısı varsa, a ve b vektörleri eşdoğrusaldır;
• durum 2 . A ve b vektörleri, eşit oranlarda koordinatlarla eşdoğrusaldır:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• durum 3 . Vektör çarpımının ve sıfır vektörünün eşit olması koşuluyla a ve b vektörleri eşdoğrusaldır:

bir ∥ b ⇔ bir , b = 0

Açıklama 1

2. koşul vektör koordinatlarından biri sıfır ise uygulanamaz.

Açıklama 2

Koşul 3 sadece uzayda verilen vektörlere uygulanabilir.

Vektörlerin doğrusallık çalışması için problem örnekleri

Eşdoğrusallık için a \u003d (1; 3) ve b \u003d (2; 1) vektörlerini inceliyoruz.

Nasıl karar verilir?

Bu durumda eşdoğrusallığın 2. koşulunu kullanmak gerekir. Verilen vektörler için şöyle görünür:

Eşitlik yanlış. Bundan a ve b vektörlerinin doğrusal olmadığı sonucuna varabiliriz.

Cevap : bir | | b

Örnek 2

Vektörlerin eşdoğrusal olması için a = (1 ; 2) ve b = (- 1 ; m) vektörünün hangi m değeri gereklidir?

Nasıl karar verilir?

İkinci eşdoğrusal koşulu kullanarak, koordinatları orantılıysa vektörler eşdoğrusal olacaktır:

Bu, m = - 2 olduğunu gösterir.

Cevap: m = - 2 .

Vektör sistemlerinin lineer bağımlılığı ve lineer bağımsızlığı için kriterler

Bir vektör uzayındaki vektörler sistemi, yalnızca sistemin vektörlerinden biri sistemin geri kalan vektörleri cinsinden ifade edilebiliyorsa lineer olarak bağımlıdır.

Kanıt

Sistem e 1 , e 2 , olsun. . . , e n lineer bağımlıdır. Sıfır vektörüne eşit olan bu sistemin lineer kombinasyonunu yazalım:

1 e 1 + 2 e 2 + . . . + bir n e n = 0

kombinasyonun katsayılarından en az birinin sıfıra eşit olmadığı.

Bir k ≠ 0 k ∈ 1 , 2 , olsun. . . , n .

Eşitliğin her iki tarafını sıfır olmayan bir katsayı ile böleriz:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (bir k - 1 bir n) e n = 0

belirtmek:

A k - 1 a m , burada m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

Bu durumda:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + βn e n = 0

veya e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Sistemin vektörlerinden birinin sistemin diğer tüm vektörleri cinsinden ifade edildiği sonucu çıkar. Kanıtlanması gereken şey buydu (p.t.d.).

yeterlilik

Vektörlerden birinin sistemin diğer tüm vektörleri cinsinden doğrusal olarak ifade edilmesine izin verin:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1+ . . . + γ n en n

e k vektörünü bu eşitliğin sağ tarafına aktarıyoruz:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1+ . . . + γ n en n

e k vektörünün katsayısı - 1 ≠ 0'a eşit olduğundan, e 1 , e 2 , vektörlerinden oluşan bir sistemle sıfırın önemsiz olmayan bir temsilini elde ederiz. . . , en n ve bu da, verilen vektör sisteminin doğrusal olarak bağımlı olduğu anlamına gelir. Kanıtlanması gereken şey buydu (p.t.d.).

Sonuç:

• Bir vektör sistemi, vektörlerinden hiçbiri sistemin diğer tüm vektörleri cinsinden ifade edilemediğinde doğrusal olarak bağımsızdır.
• Bir boş vektör veya iki eşit vektör içeren bir vektör sistemi lineer olarak bağımlıdır.

Lineer bağımlı vektörlerin özellikleri

1. 2 ve 3 boyutlu vektörler için şu koşul yerine getirilir: iki doğrusal bağımlı vektör eşdoğrusaldır. İki eşdoğrusal vektör doğrusal olarak bağımlıdır.
2. 3 boyutlu vektörler için şu koşul yerine getirilir: doğrusal olarak bağımlı üç vektör eş düzlemlidir. (3 eş düzlemli vektör - lineer bağımlı).
3. n-boyutlu vektörler için şu koşul sağlanır: n + 1 vektörler her zaman lineer bağımlıdır.

Vektörlerin doğrusal bağımlılığı veya doğrusal bağımsızlığı için problem çözme örnekleri

a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 vektörlerini doğrusal bağımsızlık için kontrol edelim.

Karar. Vektörler lineer bağımlıdır çünkü vektörlerin boyutu vektör sayısından azdır.

Örnek 4

a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 vektörlerini doğrusal bağımsızlık için kontrol edelim.

Karar. Doğrusal kombinasyonun sıfır vektörüne eşit olacağı katsayıların değerlerini buluyoruz:

x 1 a + x 2 b + x 3 c 1 = 0

Vektör denklemini doğrusal bir biçimde yazıyoruz:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Bu sistemi Gauss yöntemini kullanarak çözüyoruz:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

2. satırdan 1.'yi, 3. - 1.'den çıkarıyoruz:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

2. satırı 1. satırdan çıkarın, 2. satırı 3. satıra ekleyin:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Çözümden, sistemin birçok çözümü olduğu sonucu çıkar. Bu, a , b , c doğrusal kombinasyonunun sıfır vektörüne eşit olduğu x 1 , x 2 , x 3 gibi sayıların değerlerinin sıfır olmayan bir kombinasyonu olduğu anlamına gelir. Dolayısıyla a , b , c vektörleri lineer bağımlı. ​​​​​​​

Metinde bir hata fark ederseniz, lütfen vurgulayın ve Ctrl+Enter tuşlarına basın.

Vektör Uzayı. Vektör uzaylarının örnekleri ve en basit özellikleri Bir vektör sisteminin lineer bağımlılığı ve bağımsızlığı Sonlu bir vektör sisteminin temeli ve rankı.

P alanı üzerindeki doğrusal veya vektör uzayı L(P), üzerinde işlemlerin tanıtıldığı boş olmayan bir L kümesidir:

1. toplama, yani kümenin her eleman çiftine aynı kümenin x + yϵL ile gösterilen bir elemanı atanır.

2. bir skaler ile çarpma (yani, P alanının bir elemanı), yani herhangi bir λ ϵ P elemanı ve herhangi bir x ϵ L elemanı, L(P'den gelen, λx ϵ L() ile gösterilen tek bir elemanla ilişkilendirilir. P).

Bu durumda, operasyona aşağıdaki koşullar uygulanır:

1. x+ y= y+ x, herhangi bir x,y ϵ L için.

2.x+ (y + z) = (x + y) + z, x, y, z ϵ L. (büzülmenin çağrışımı)

3. böyle var θ ϵ L, hangi x+ θ =x için herhangi bir x ϵ L (toplamaya göre nötr bir elemanın varlığı), özellikle, boş değildir;

4. Herhangi bir x ϵ L için bir -x ϵ L elemanı vardır, öyle ki x+(-x)= θ (toplamaya göre zıt elemanın varlığı).

5.(αβ)х=α(βх), (bir skaler ile çarpmanın ilişkilendirilebilirliği)

6.1*x=x (birlik: P alanının bir nötr (çarpma ile) elemanı ile çarpma vektörü korur).

7.(α+ β)* x= α* x+ β*x, (skalerlerin eklenmesine göre bir vektör ile çarpmanın dağılımı);

8. α * (x + y) = a*x+ α *y, (vektör toplamaya göre bir skaler ile çarpmanın dağılımı).

L kümesinin elemanlarına vektör, P alanının elemanlarına skaler adı verilir. Özellikler 1-4, değişmeli grubun aksiyomlarıyla örtüşür.

En basit azizler:

1. Bir vektör uzayı, toplama yoluyla bir değişmeli gruptur.

2. Herhangi bir x ϵ L için, karşıt eleman -x ϵ L tektir

3. 0*X=θ, herhangi bir x ϵ L

4. 1*(-x)=-x herkes için x ϵ L

5.α * θ = θ ,herhangi bir α içinϵ L

Bir VP örneği yav-Xia m \ toplama ve çarpma işlemlerinin doğal bir tanımı ile aynı sıradaki gerçek bileşenlere sahip matrislerde. Madde numarası başına matrisler

Doğrusal bağımlılık \ (değil) bir vektör sistemi (tanımlar, özellikler)

Teorem. (Bir vektör sisteminin lineer bağımlılığı için gerekli ve yeterli bir koşul.)

Bir vektör uzayındaki vektörler sistemi, ancak ve ancak sistemin vektörlerinden birinin bu sistemin diğer vektörleri cinsinden doğrusal olarak ifade edilmesi durumunda doğrusal olarak bağımlıdır.

Kanıt. İhtiyaç. e 1 ..e n sistemi lineer bağımlı olsun. Daha sonra, tanım gereği, boş vektörü önemsiz olmayan bir şekilde temsil eder, yani. sıfır vektörüne eşit olan bu vektörler sisteminin önemsiz olmayan bir lineer kombinasyonu vardır:

α 1 e 1 +..+ α n e n = 0, burada bu lineer kombinasyonun katsayılarından en az biri sıfır değildir. α k ≠0 ,kϵ 1,2…n Önceki eşitliğin her iki bölümünü de bu sıfır olmayan katsayıya bölün (yani α k -1 ile çarpın *(α 1 e 1 +..+ αa n e n) =0

Belirtin: α k -1 α m =β m burada mϵ 1,2…,k-1,k+1,..,n Sonra β 1 ​​e 1+ … +β 1 e n =0 yani. sistemin vektörlerinden biri, bu sistemin diğer vektörleri cinsinden doğrusal olarak ifade edilir, vb.

yeterlilik. Sistemin vektörlerinden biri bu sistemin diğer vektörleri cinsinden lineer olarak ifade edilsin: e k =γ 1 e 1+..+ γ n e n

e k vektöründeki katsayı -1≠0'a eşit olduğundan, e 1 ..e n vektörlerinden oluşan bir sistemle sıfırın önemsiz olmayan bir temsiline sahibiz, bu da bu vektör sisteminin doğrusal olarak bağımlı olduğu anlamına gelir, vb.

Teorem kanıtlanmıştır.

Sonuç.

1. Bir vektör uzayındaki vektörler sistemi, ancak ve ancak sistemin vektörlerinden hiçbiri bu sistemin diğer vektörleri cinsinden doğrusal olarak ifade edilmemişse, doğrusal olarak bağımsızdır.

2. Bir sıfır vektör veya iki eşit vektör içeren bir vektörler sistemi lineer bağımlıdır.

Sonuç.

Bir vektörden oluşan bir sistem, ancak ve ancak bu vektör sıfırdan farklıysa lineer olarak bağımsızdır.

Bir baz, bir vektör uzayındaki bir vektörler kümesidir, öyle ki bu uzayın herhangi bir vektörü, bu küme temel vektörlerinden vektörlerin lineer bir kombinasyonu olarak benzersiz bir şekilde temsil edilebilir.

Belirli bir vektör sisteminin herhangi bir maksimum lineer bağımsız alt sistemine dahil edilen vektörlerin sayısına denir. rütbe sistemler.

Teorem.İki sistem verilsin P- boyutlu vektörler:

a 1 ,a 2,¼, a r (9)

b 1 ,b 2,¼, bs, (10)

lineer olarak bağımsız olması gerekmez ve sistemin (9) sırası sayıya eşittir k, sistemin rankı (10) sayıdır ben. Birinci sistem, ikincisi cinsinden doğrusal olarak ifade edilirse, o zaman k £ l. Eğer bunlar sistemler eşdeğerdir, o zamanlar k = l.

Uzayın maksimum lineer bağımsız alt kümesinin eleman sayısı (kardinalite) bu alt kümenin seçimine bağlı değildir ve uzayın rankı veya boyutu olarak adlandırılır ve bu alt kümenin kendisine temel denir.