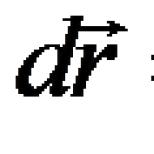Rijit bir cisme uygulanan kuvvetlerin işi. Bir rijit cisme uygulanan kuvvetin işi ve gücü Dönen bir cisme uygulanan sabit bir kuvvetin işi

Bir kuvvetin yer değiştirme üzerindeki temel işi (Şekil 3.22), kuvvetin skaler ürünü ve uygulama noktasının temel yer değiştirmesidir:

a, vektörlerin yönleri arasındaki açıdır ve

Gibi o zaman temel işin başka bir ifadesini yazabiliriz:

İlköğretim çalışmaları için birkaç ifade daha yazabilirsiniz:

Temel çalışma formüllerinden, bu niceliğin pozitif (a açısı dar), negatif (a açısı geniş) veya sıfıra eşit (a açısı dik) olabileceği sonucu çıkar.

Tam güç çalışması. Bir noktadan yer değiştirme üzerine bir kuvvetin toplam işini belirlemek için M 0 ila M Bu hareketi ikiye bölelim n her biri sınırda temel hale gelen yer değiştirmeler. Daha sonra kuvvetin işi ANCAK:

nerede dA k- üzerinde çalışmak k-inci temel yer değiştirme.

Yazılan toplam integraldir ve yer değiştirme üzerine eğri boyunca alınan eğrisel bir integral ile değiştirilebilir. M 0 M. Sonra

veya

saat nerede t=0 bir noktaya karşılık gelir M 0 ve zaman t- nokta M.

Temel ve eksiksiz işin tanımından şu şekildedir:

1) herhangi bir yer değiştirme üzerindeki bileşke kuvvetin işi, bu yer değiştirme üzerindeki bileşen kuvvetlerinin işinin cebirsel toplamına eşittir;

2) tam yer değiştirme üzerindeki kuvvetlerin işi, tüm yer değiştirmenin herhangi bir şekilde bölündüğü bileşen yer değiştirmeleri üzerindeki aynı kuvvetin işinin toplamına eşittir.

Gücün gücü. Bir kuvvetin gücü, birim zamanda yapılan iştir.

ya da bunu göz önünde bulundurarak

kuvvet gücü kuvvetin skaler ürününe ve uygulandığı noktanın hızına eşit bir değerdir.

Böylece, sabit güçte, hızdaki bir artış, kuvvette bir azalmaya yol açar ve bunun tersi de geçerlidir. Güç birimi Watt: 1W=1J/sn.

Sabit bir eksen etrafında dönen bir cisme bir kuvvet uygulanırsa, gücü eşittir.

Bir çift kuvvetin gücü de benzer şekilde belirlenir.

3.3.4.3. Bir kuvvetin işini hesaplama örnekleri

kuvvetin toplam işi

nerede h- noktanın düştüğü yükseklik.

Böylece yerçekimi tarafından yapılan iş, nokta alçalırken pozitif, yükselirken negatiftir. Yerçekimi işi, noktalar arasındaki yörüngenin şekline bağlı değildir. M 0 ve M 1 .

Lineer elastikiyet kuvvetinin işi. Lineer elastikiyet kuvvetine Hooke yasasına göre hareket eden kuvvet denir (Şekil 3.24):

kuvvetin sıfır olduğu denge noktasından düşünülen noktaya çizilen yarıçap vektörü nerede M; ile sabit bir sertlik katsayısıdır.

Bir noktadan hareket eden kuvvetin yaptığı iş M 0 nokta M 1 formül tarafından belirlenir

Entegre ederek, elde ederiz

(3.27)

(3.27) formülüne göre, yayların lineer elastik kuvvetinin işi, noktadan herhangi bir yol boyunca hareket ederken hesaplanır. M 0 , burada başlangıç ​​gerilimi eşittir kesinlikle M 1 , burada deformasyon sırasıyla eşittir Yeni gösterimde formül (3.27) şu şekli alır:

Dönen bir rijit cisme uygulanan kuvvetin işi. Katı bir cisim sabit bir eksen etrafında döndüğünde, bir noktanın hızı M Euler formülü kullanılarak hesaplanabilir, bkz. 3.25:

Daha sonra kuvvetin temel işi formülle belirlenir.

Karışık vektör ürün özelliğini kullanma
alırız

Gibi - nokta etrafındaki kuvvet momenti Ö. Verilen - dönme ekseni etrafındaki kuvvet momenti Öz ve ω dt=dφ, sonunda şunu elde ederiz:

dA=mzdφ.

Sabit bir eksen etrafında dönen bir cismin herhangi bir noktasına uygulanan bir kuvvetin temel işi, kuvvetin dönme ekseni etrafındaki momenti ile cismin dönme açısının diferansiyeli çarpımına eşittir.

Tam çalışma:

Özel durumda ne zaman , iş formül tarafından belirlenir

burada j, kuvvetin işinin hesaplandığı cismin dönme açısıdır.

Katı bir cismin iç kuvvetlerinin işi. Katı bir cismin iç kuvvetlerinin yaptığı işin, herhangi bir yer değiştirme için sıfıra eşit olduğunu ispatlayalım. Tüm iç kuvvetlerin temel işlerinin toplamının sıfıra eşit olduğunu kanıtlamak yeterlidir. Vücudun herhangi iki noktasını düşünün M 1 ve M 2 (Şekil 3.26). İç kuvvetler, vücudun noktalarının etkileşim kuvvetleri olduğundan, o zaman:

Kuvvet tarafından yönlendirilen bir birim vektörü tanıtıyoruz.

Temel kuvvetlerin toplamı ve eşittir

Vektörlerin skaler çarpımlarını parantez içinde genişleterek şunu elde ederiz:

Bir rijit cismin herhangi iki noktasının hızlarının, bu noktaları birleştiren düz bir çizgi yönünde izdüşümlerinin, rijit bir cismin herhangi bir hareketi için birbirine eşit olduğu kinematikte kanıtlandığından, parantez içindeki fark ortaya çıkan ifade, özdeş değerlerin farkıdır, yani. sıfıra eşit bir değer.

3.3.4.4. Bir noktanın kinetik enerjisindeki değişime ilişkin teorem

Kütlesi olan bir madde noktası için m, bir kuvvetin etkisi altında hareket eden, dinamiğin temel yasası şu şekilde temsil edilebilir:

Bu ilişkinin her iki parçasını noktanın yarıçap vektörünün diferansiyeli ile skaler olarak çarparsak,

veya

Verilen - temel güç işi,

(3.28)

Formül (3.28), diferansiyel formda bir nokta için kinetik enerjideki değişime ilişkin teoremi ifade eder.

Bir noktanın kinetik enerjisinin diferansiyeli, o noktaya etki eden kuvvetin temel işine eşittir.

Eğer eşitliğin (3.28) her iki kısmı noktadan bütünleştirilirse M 0 nokta M(bkz. Şekil 3.22), sonlu biçimde bir noktanın kinetik enerjisindeki değişim hakkında bir teorem elde ederiz:

Herhangi bir yer değiştirmede bir noktanın kinetik enerjisindeki değişiklik, aynı yer değiştirmede o noktaya etki eden kuvvetin işine eşittir.

3.4.4.5. Sistemin kinetik enerjisindeki değişim ile ilgili teorem

Sistemin her noktası için kinetik enerjideki değişim teoremi şu şekilde ifade edilebilir:

Sistemin tüm noktaları üzerinde bu bağıntıların sağ ve sol kısımlarını toplayarak ve toplamın işaretinden diferansiyelin işaretini alarak şunu elde ederiz:

veya

nerede sistemin kinetik enerjisidir; sırasıyla dış ve iç kuvvetlerin temel işidir.

Formül (3.29) sistemin kinetik enerjisindeki değişime ilişkin teoremi diferansiyel biçimde ifade eder.

Sistemin kinetik enerjisinden farkı, sisteme etki eden tüm dış ve iç kuvvetlerin temel işlerinin toplamına eşittir.

(3.29)'un her iki kısmı sistemin iki konumu arasında entegre edilirse - kinetik enerjinin eşit olduğu ilk ve son T 0 ve T, sonra, toplama ve integrasyon sırasını değiştirerek şunları elde ederiz:

veya

nerede sistemin bir noktası için bir dış kuvvetin işidir mk başlangıç ​​konumundan bitiş konumuna hareket ederken mk; noktaya etki eden iç kuvvetin işidir. mk.

Formül (3.30), sistemin kinetik enerjisindeki değişime ilişkin teoremi sonlu veya integral formda ifade eder.

Sistemin bir konumdan diğerine hareket ederken kinetik enerjisindeki değişim, aynı yer değiştirmeye sahip sistem noktalarının karşılık gelen yer değiştirmeleri üzerine etkiyen tüm dış ve iç kuvvetlerin işinin toplamına eşittir. sistem.

Öteleme veya dönme hareketi yapan katı bir cismin herhangi bir noktasına uygulanan kuvvetin işini ve gücünü belirlemek için formülleri düşünün.

1. Öteleme hareketinde rijit bir cisme uygulanan kuvvetin işi ve gücü.

Rastgele bir noktada uygulanan bir kuvvetin etkisi altında eylemsiz bir referans çerçevesine göre öteleme hareketi yapan katı bir cisim düşünün (Şekil 24).

Katı bir cismin öteleme hareketi durumunda, tüm noktaları aynı büyüklük ve yöndeki hızlarla hareket eder. Vücudun hızını gösterelim.

(4.31) formülünü kullanarak şunu elde ederiz:

katı cismin keyfi bir noktasının yarıçap vektörünün diferansiyeli nerede .

Pirinç. 24. Bir kuvvetin etkisi altında katı bir cismin öteleme hareketi

(4.49) ile bölme dt, öteleme hareketi yapan bir cisme etki eden kuvvetin gücünü belirlemek için bir ifade elde ederiz:

hız kuvveti vektörleri arasındaki açı nerede.

Yani, katı bir cismin öteleme hareketindeki kuvvetin gücü, rijit cismin kuvvet vektörü ve hız vektörünün skaler ürünü olarak tanımlanır.

Noktanın bazı sonlu yer değiştirmelerinde integral alma (4.49) M başlangıç ​​​​pozisyonundan M 0 konumuna M 1, bu yer değiştirmede cisme etki eden kuvvetin toplam işini elde ederiz.

2. Dönme hareketi yapan katı bir cisme uygulanan kuvvetin işi ve gücü.

Sabit bir dikey eksen etrafında katı bir cismin dönüşünü düşünün Öz bu cismin keyfi bir noktasında uygulanan bir kuvvetin etkisi altında M(Şek. 25).

Pirinç. 25. Sabit bir cismin sabit bir eksen etrafında dönmesi

nokta konumu M eksenlerde oksijen yarıçap vektörü tarafından belirlenir. Nokta hızı M hareket yörüngesine teğet olarak yönlendirilir (dönme ekseninde ortalanmış bir daire). Bu hızın vektörü, katı cisim kinematiğinden bilinen Euler vektör formülü ile belirlenebilir.

katı cismin açısal dönme hızının vektörü nerede.

(4.32) formülünü kullanarak şunu elde ederiz:

Karışık vektör ürünündeki faktörleri dairesel bir sırayla değiştirerek,

merkeze göre vektör kuvvet momenti nerede Ö.

Momentum ve açısal hız vektörleri arasındaki açı.

Verilen:

1. - dönme eksenine göre kuvvet momenti Öz.

2. ve bu nedenle,

sonunda anladık

Böylece, Sabit bir eksen etrafında dönen katı bir cismin herhangi bir noktasına uygulanan bir kuvvetin temel işi, bu kuvvetin dönme ekseni etrafındaki momenti ile cismin dönme açısının diferansiyeli çarpımına eşittir.

Vücut φ açısı boyunca döndüğünde kuvvetin toplam işini belirlemek için (4.53) ifadesini entegre ederek,

durumunda, toplam iş formülle belirlenebilir.

burada φ kuvvetin işinin belirlendiği cismin dönme açısıdır.

Momentin yönü ve açısal hız aynı ise kuvvetin yaptığı iş pozitif, aksi halde negatif kabul edilir.

Katı bir cismin bir eksen etrafında dönmesi sırasındaki kuvvetin gücünü belirleyelim. (4.40) formülünü kullanarak, şunu elde ederiz:

yani Dönen bir katı cisme uygulanan kuvvetin gücü, dönme ekseni etrafındaki kuvvet momenti ile cismin açısal hızının çarpımı olarak tanımlanır. . Gücün işareti, iş işaretine benzer şekilde belirlenir.

Mekanik bir sistemin parçası olan bir rijit cismin M1 ve M2 iki keyfi noktasını ele alalım. İnşaatları yapalım (bkz. şek.14.13).

Iç kuvvetler PJ 1 , PJ 2 etki ve tepki eşitliği yasası temelinde bir noktadan diğerine hareket eden, mutlak değerde eşit ve zıt yönlüdür. PJ1 = - PJ2 .

Belirli bir anda noktaların hızları sırasıyla u 1 ve u 2'ye eşit olsun ve zaman aralığı boyunca vektörler boyunca artışlar şöyle olsun: ds 1 \u003d u 1 dt, ds 2 \u003d u 2 dt.

Düz bir şeklin noktalarının hızları üzerindeki teoremin 1. sonucu temelinde, hız vektörlerinin M 1 M2 segmentinin yönündeki izdüşümleri eşit olduğundan, o zaman bu noktalar eşit olacaktır.

Bu nedenle, dikkate alınan yer değiştirme üzerindeki 2 iç kuvvetin temel işlerinin toplamını hesaplayarak ve eşitliklerini ve zıt yönlerini dikkate alarak elde ederiz.

P J 1 ds 1 cos(P J1,sen 1) + PJ 2 ds 1 cos(P J2,sen 2)= P J 1 * M 1 M' 1 - P J 1 * M 2 M' 2 = 0.

Her bir iç kuvvet bir diğerine karşılık geldiği için, mutlak değerde eşit ve zıt olduğundan, tüm iç kuvvetlerin temel işlerinin toplamı sıfıra eşittir.

Nihai yer değiştirme, bir dizi temel yer değiştirmedir ve bu nedenle

ve j = 0,

onlar. katı bir cismin yer değiştirmelerinden herhangi biri üzerindeki iç kuvvetlerinin işinin toplamı sıfıra eşittir.

Katı bir cismin öteleme hareketi.

Katı bir cismin öteleme hareketinde, tüm noktalarının yörüngeleri aynı ve paraleldir. Bu nedenle, temel yer değiştirmelerin vektörleri geometrik olarak eşittir.

Temel kuvvet işi P E ben

dA E ben =P ben r.

Tüm güç için olacak

d A=Sd A E ben = SP ben r= d r SP E = d r TEKRAR .

Buradan,

dA=d r TEKRAR . (14-46)

İlerleyen katı bir cisme uygulanan kuvvetlerin temel işi, ana kuvvet vektörünün temel işine eşittir..

bir= . (14-47)

Sabit bir eksen etrafında dönen katı bir cisme uygulanan kuvvetlerin temel işi, dönme ekseni etrafındaki dış kuvvetlerin ana momenti ile dönme açısının artışının çarpımına eşittir..

Son yolculukta çalışmak

SA ben = , (14-48)

dönme ekseni etrafındaki dış kuvvetlerin ana momenti nerede.

Ana moment sabit ise, o zaman

SA ben = Ez = Ez (j 2 - j 1).(14-49)

Bu durumda, son yer değiştirme üzerindeki işin toplamı, dış kuvvetlerin ana momentinin ürününe ve gövdenin dönme açısındaki son değişikliğin ürününe eşittir.

sonra güç

N= = M E z dj/dt= M E z w.(14-50)

Genel hareket durumunda, serbest bir rijit cisme uygulanan dış kuvvetlerin temel işi şuna eşittir:

dA=SdAi=R E d r O + M E W da,(14-51)

nerede M EW- anlık eksene göre dış kuvvetlerin ana momenti; da- anlık eksene göre temel dönüş açısı.

14.10. yuvarlanma direnci.

Duran yatay bir düzlemde bulunan silindirik bir silindirde (Şekil 14.14, a), karşılıklı olarak dengelenmiş iki kuvvet etki eder: silindirin ağırlığı G ve normal düzlem reaksiyonu N = -G .

Yatay bir kuvvetin etkisi altındaysa R C silindirinin merkezine uygulandığında, düzlem boyunca kaymadan yuvarlanır, ardından kuvvetler G,N yuvarlanmayı önleyen bir çift kuvvet oluşturur (Şekil 14.14, b).

Bu kuvvet çiftinin ortaya çıkması, silindirin ve düzlemin temas yüzeylerinin deformasyonundan kaynaklanmaktadır. Reaksiyon eylem satırı N G kuvvetinin etki çizgisinden bir d mesafesi kadar kaydırılır.

Bir çift kuvvetin momenti G,N yuvarlanma direnci momenti denir. Değeri ürün tarafından belirlenir

M direnci = Nd. (14-52)

Yuvarlanma katsayısı doğrusal birimlerle ifade edilir, yani. [d]= bkz. örneğin çelik ray üzerinde çelik bandaj d= 0,005 cm; çelik üzerine ahşap d\u003d 0,03-0,04 cm.

En küçük yatay kuvveti tanımlayalım R pistin ortasına uygulanır.

Silindirin yuvarlanmaya başlaması için, P kuvveti ve F sc yapışma kuvveti tarafından oluşturulan kuvvet çiftinin momenti, direnç momentinden, yani.

PR>Nd.

Neresi P>Nd/R.

Çünkü burada N=G, o zaman

Son yer değiştirmede iç kuvvetlerin işi sıfırdır.

Ötelemeli olarak hareket eden bir cisme etki eden bir kuvvetin işi, bu kuvvetin ürününe ve doğrusal yer değiştirmenin artışına eşittir.

Dönen bir cisme etki eden kuvvetin işi, bu kuvvetin dönme ekseni etrafındaki momenti ile dönme açısının artışının çarpımına eşittir: ; . Güç:
.

Çeşitli hareket türleri için mekanik bir sistemin kinetik enerjisi.

Mekanik bir sistemin kinetik enerjisi- sistemin tüm noktalarının kinetik enerjilerinin toplamına eşit bir skaler: .

İleri hareket için:

Dönerken:

Düzlem paralel hareket ile: burada d, kütle merkezinden MCS'ye olan mesafedir

27. Maddi bir noktanın kinetik enerjisindeki değişime ilişkin teorem.

Maddi bir noktanın kinetik enerjisi- bir noktanın kütlesinin çarpımının yarısına ve hızının karesine eşit bir skaler.

Dinamiklerin temel denklemi: , temel yer değiştirme ile çarpın: ; ; . Ortaya çıkan ifadeyi entegre etme:

teorem: bir yer değiştirmede bir madde noktasının kinetik enerjisindeki değişiklik, aynı yer değiştirmede o noktaya etki eden kuvvetin işine eşittir.

Mekanik bir sistemin kinetik enerjisindeki değişime ilişkin teorem.

İç kuvvetlerin işi sıfır olduğuna göre:
.

teorem: Sonlu bir yer değiştirmede mekanik bir sistemin kinetik enerjisindeki değişiklik, aynı yer değiştirmede dış kuvvetlerin yaptığı işin toplamına eşittir.

Mekanik bir sistem için olası yer değiştirmeler ilkesi.

; , mekanik sistemin noktalarına dayatılan kısıtlamaların iki yönlü, durağan, holonomik ve ideal olmasına izin verin, o zaman: .

Olası hareketler ilkesi - Lagrange ilkesi- iki taraflı, durağan, holonomik ve ideal kısıtlamalara sahip mekanik bir sistemin dengesi için, verilen kuvvetlerin olası bir yer değiştirme üzerindeki çalışmalarının cebirsel toplamının sıfıra eşit olması gerekli ve yeterlidir.

Maddi bir nokta için d'Alembert ilkesi.

Hareketli bir malzeme noktasına uygulanan tüm kuvvetlerin geometrik toplamı ve bu noktanın eylemsizlik kuvvetleri sıfıra eşittir.

Serbest olmayan bir mekanik sistem için d'Alembert ilkesi.

Hareketli, serbest olmayan bir mekanik sistemde, herhangi bir zamanda her malzeme noktası için, kendisine uygulanan kuvvetlerin geometrik toplamı, kuplaj reaksiyonları ve atalet kuvvetleri sıfıra eşittir. İfadenin her iki kısmını da r i ile çarparak şunu elde ederiz: ;
.

, verilen kuvvetlerin, kuplaj reaksiyonlarının ve atalet kuvvetlerinin koordinat eksenleri etrafındaki momentlerinin toplamı sıfıra eşittir.

Katı bir cismin noktalarının atalet kuvvetlerini en basit forma getirmek.

Katı bir cismin noktalarının atalet kuvvetleri sistemine, statikte ele alınan Punchon yöntemi uygulanabilir. Daha sonra herhangi bir atalet kuvvetleri sistemi, atalet kuvvetlerinin ana vektörüne ve ana atalet kuvvetleri momentine indirgenebilir.

Öteleme hareketinde: Ф=-ma (katı bir cismin öteleme hareketinde, noktalarının atalet kuvvetleri, ivme ile, vücut kütlesinin ürününe mutlak değerde eşit olan ana atalet kuvvetlerinin ana vektörüne indirgenir. bu merkeze uygulanan ve kütle merkezinin zıt ivmesine doğru yönlendirilen kütle merkezi).

Dönme hareketi sırasında: M = -Iε (rijit bir cismin dönme hareketi sırasında, noktalarının atalet kuvvetleri, dönme kuvvetlerine göre vücudun atalet momentinin ürününe eşit olan ana atalet kuvvetleri momentine indirgenir. ve açısal ivme Bu moment zıt açısal ivmeye yöneliktir).

Düzlem hareketi için: Ф=-ma M=-Iε (rijit bir cismin düz hareketi için, noktalarının atalet kuvvetleri ana vektöre ve ana atalet kuvvetleri momentine indirgenir).

Dinamiğin genel denklemi. d'Alembert-Lagrange ilkesi.

d'Alembert ilkesi: å(P i + R ben + Ф i) = 0; å(P i + R ben + Ф i)Dr i = 0, varsayıyoruz. mekanik sisteme dayatılan kısıtlamaların iki yönlü, durağan, holonomik ve ideal olduğuna göre: å(R i × Dr i) = 0;

å(P i + Ф i)Dr ben = 0 - genel dinamik denklemi- iki yönlü, durağan, holonomik ve ideal kısıtlamalara sahip mekanik bir sistemin hareketi için, verilen kuvvetlerin işi ve sistemin noktalarının herhangi bir olası yer değiştirme üzerindeki atalet kuvvetlerinin toplamı sıfıra eşittir.

F 1 J ve F 2 J iki iç kuvvetinin temel işlerinin toplamını hesaplayarak,

alırız

F1 J dS1 cos(P1 J ,υ 1 ) + F2 J dS2 cos(P2 J ,υ 2 ) = F1 ′ M1 M1 ′ − F1 M 2 M 2 ′

çünkü her bir iç kuvvet diğerine karşılık gelir, mutlak değerde ona eşit ve zıt yönde, o zaman tüm iç kuvvetlerin temel işlerinin toplamı da sıfıra eşittir.

δ A J = ∑ δ A ben J = 0

Son hareket, bir dizi temel değişkendir.

böylece AJ = 0, yani, katı bir cismin yer değiştirmelerinden herhangi biri üzerindeki iç kuvvetlerinin işinin toplamı sıfıra eşittir.

2.5.2. Aşamalı olarak hareket eden bir cisme uygulanan dış kuvvetlerin işi

Vücudun her noktasına dış ve iç kuvvetler uygulanır (Şekil 18). Herhangi bir yer değiştirme üzerindeki iç kuvvetlerin işi sıfır olduğundan, sadece F 1 E , F 2 E ... F n E dış kuvvetlerinin işini hesaplamak gerekir. ilerici ile

tüm noktaların yörüngeleri aynıdır ve temel yer değiştirme vektörleri geometrik olarak eşittir, yani.

dri = dr = dr.

F i E kuvvetinin temel işi

δ A iE = F ben E dr c .

Tüm dış kuvvetlerin temel işi

δ AE = ∑ δ Ai E = ∑ F ben E drc = drc ∑ Fi E = R E dr c ,

burada R E, dış kuvvetlerin ana vektörüdür.

Son yolculukta çalışmak

AE = ∫ R E drc .

Katı bir cismin öteleme hareketi sırasındaki kuvvetlerin işi, dış kuvvetlerin ana vektörünün kütle merkezinin temel yer değiştirmesi üzerindeki çalışmasına eşittir.

2.5.3. Dönen bir cisme uygulanan dış kuvvetlerin işi

Sabit bir Z ekseni etrafında dönen katı bir cisme F 1 E , F 2 E … F i E … F n E dış kuvvetlerinin uygulandığını varsayalım (Şekil 19).

Yarıçapı R i olan bir daireyi tanımlayan, M i noktasına uygulanan bir F i E kuvvetinin işini hesaplayalım. F i E kuvvetini, M i noktasının yörüngesinin doğal eksenleri boyunca yönlendirilmiş üç bileşene ayıralım.

E F 1

Mi dSi

Yerleştirmek

Z M1 (x1 ,y1, z1 )

M2 (x2 ,y2 , z2 )

Vücudun bir d ϕ açısı boyunca temel bir dönüşü ile, M i noktası bir dS i = R i d ϕ yayı tanımlar. Bu harekette iş, kuvvetin yalnızca teğetsel bileşenidir ve hız vektörüne dik olan E ve F ib E'deki F kuvvetinin bileşenlerinin işi sıfıra eşittir.

δ A i E = F ben τ E dS ben = F ben τ E R ben d ϕ = M ben E τ d ϕ = M iz E d ϕ , çünkü F i E kuvvetinin normal ve binormal bileşenlerinin Z eksenine göre momentleri sıfır elemana eşittir

katı bir cisme uygulanan tüm kuvvetlerin zihinsel çalışması

δ AE = ∑ δ Ai E = ∑ M iz E dϕ = dϕ ∑ Miz E = M z E dϕ .

Böylece, dönen bir rijit cisme uygulanan dış kuvvetlerin temel işi şuna eşittir:

δ AE = M z E dϕ .

Vücudun son dönüşünde, dış kuvvetin işi eşittir

AE = ∫ M z E dϕ .

Dış kuvvetlerin ana momenti M z E = const ise, dış kuvvetlerin nihai yer değiştirme üzerindeki işi A = M z E (ϕ 2 − ϕ 1 ) olur.

Rijit bir cismin dönme hareketi sırasındaki iş, temel açısal yer değiştirme üzerindeki dönme ekseni etrafındaki dış kuvvetlerin ana momentinin çalışmasına eşittir.

2.6. Yerçekimi işi

Kütlesi m olan bir nokta yerçekimi etkisi altında M 1 (x 1, y 1, z 1) konumundan M 2 (x 2, y 2, z 2) konumuna hareket etsin (Şekil 20).

Bir kuvvetin temel işi, kuvvet vektörü F (X ,Y ,Z ) ile temel yer değiştirme vektörünün dr (dx,dy,dz ) skaler çarpımı olarak hesaplanır.

δ A = F dr = Xdx + Ydy + Zdz,

nerede X ,Y ,Z - F kuvvetinin izdüşümleri,

dx,dy,dz - dr yer değiştirme vektörünün x, y,z eksenleri üzerindeki izdüşümleri. Yerçekimi etkisi altında hareket ederken

A \u003d ± mgh.

Nokta indirilirse (yörünge türünden bağımsız olarak), yani. z2< z 1 , работа силы тяжести положительна, если точка поднимается, работа силы тя-

jest olumsuz. Nokta yatay hareket ediyorsa (z 2 = z 1 ), yerçekimi tarafından yapılan iş 0'dır.

3. KİNETİK ENERJİ DEĞİŞİMİNE İLİŞKİN TEOREM

Hareket altında hareket eden, kütlesi m olan bir M malzeme noktası düşünün.

Denklemin her iki tarafını dS ile çarpın ve denklemin her iki tarafını da başlangıç ​​ve son konumlara karşılık gelen limitler dahilinde entegre edin

2

	Makale değerlendirmesi: (Henüz derecelendirme yok) Yükleniyor... Arkadaşlarınızla paylaşmak için: benzer gönderiler Bir rijit cisme uygulanan kuvvetin işi ve gücü Dönen bir cisme uygulanan sabit bir kuvvetin işi Matrislerde temel işlemler Grafiksel ve sayısal farklılaşma Birinci dereceden kısmi türevler