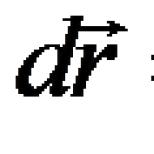Belirli bir vektör sisteminin temeli nasıl bulunur. Doğrusal bağımlılık. Vektör sisteminin temeli Temeldir

Vektörlerin doğrusal bir kombinasyonu bir vektördür
, burada λ 1 , ... , λ m keyfi katsayılardır.

vektör sistemi
buna eşit lineer kombinasyonu varsa, lineer bağımlı olarak adlandırılır. , en az bir sıfır olmayan katsayıya sahiptir.

vektör sistemi
doğrusal kombinasyonlarından herhangi birinde eşitse, doğrusal olarak bağımsız olarak adlandırılır. , tüm katsayılar sıfırdır.

Vektörler sisteminin temeli
sistemin herhangi bir vektörünün ifade edilebildiği boş olmayan lineer bağımsız alt sistemi çağrılır.

Örnek 2. Vektörler sisteminin temelini bulun = (1, 2, 2, 4),= (2, 3, 5, 1),= (3, 4, 8, -2),= (2, 5, 0, 3) ve kalan vektörleri taban cinsinden ifade edin.

Çözüm Bu vektörlerin koordinatlarını sütunlar halinde düzenlediğimiz bir matris oluşturuyoruz. Basamaklı forma getiriyoruz.

~
~
~
.

Bu sistemin temelini vektörler oluşturmaktadır. ,,, dairelerle işaretlenmiş satırların önde gelen öğelerine karşılık gelir. Bir vektör ifadesi için denklemi çöz x 1 +x2 +x4 =. Bu, matrisi orijinalden, karşılık gelen sütuna izin verilerek elde edilen bir doğrusal denklem sistemine indirgenir. , ücretsiz üyeler sütunu yerine. Bu nedenle, sistemi çözmek için, elde edilen matrisi adım adım bir biçimde kullanırız ve içinde gerekli permütasyonları yaparız.

Art arda buluyoruz:

x 1 + 4 = 3, x 1 = -1;

= -+2.

Açıklama 1. Birkaç vektörü temel üzerinden ifade etmek gerekirse, o zaman bunların her biri için karşılık gelen lineer denklem sistemi oluşturulur. Bu sistemler sadece ücretsiz üyelerin sütunlarında farklılık gösterecektir. Bu nedenle, bunları çözmek için, içinde birkaç serbest üye sütununun olacağı bir matris derlenebilir. Bu durumda, her sistem diğerlerinden bağımsız olarak çözülür.

Açıklama 2. Herhangi bir vektörü ifade etmek için, sadece kendisinden önce gelen sistemin temel vektörlerini kullanmak yeterlidir. Bu durumda matrisi yeniden şekillendirmeye gerek yoktur, doğru yere dikey bir çizgi koymak yeterlidir.

Alıştırma 2. Vektörler sisteminin temelini bulun ve vektörlerin geri kalanını bu temel üzerinden ifade edin:

a) = (1, 3, 2, 0),= (3, 4, 2, 1),= (1, -2, -2, 1),= (3, 5, 1, 2);

b) = (2, 1, 2, 3),= (1, 2, 2, 3),= (3, -1, 2, 2),= (4, -2, 2, 2);

içinde) = (1, 2, 3),= (2, 4, 3),= (3, 6, 6),= (4, -2, 1);= (2, -6, -2).

1. 3. Temel karar sistemi

Tüm serbest terimleri sıfıra eşitse, bir lineer denklem sistemine homojen denir.

Homojen bir lineer denklem sisteminin temel çözüm sistemi, çözüm kümesinin temelidir.

Homojen olmayan bir lineer denklem sistemi verilsin. Belirli bir sistemle ilişkili homojen bir sistem, tüm serbest terimleri sıfırlarla değiştirerek belirli bir sistemden elde edilen bir sistemdir.

Homojen olmayan bir sistem tutarlı ve belirsiz ise, o zaman keyfi çözümü fo o1 +  1 f o1 + ... +  k fok şeklindedir, burada f o homojen olmayan sistemin özel bir çözümüdür ve fo1 , ... , fo k ilişkili homojen sistemin temel sistem çözümleridir.

Örnek 3. Örnek 1'deki homojen olmayan sistemin belirli bir çözümünü ve ilgili homojen sistemin temel çözüm sistemini bulun.

Çözüm Örnek 1'de elde edilen çözümü vektör biçiminde yazıp, ortaya çıkan vektörü içerdiği serbest parametreler ve sabit sayısal değerler üzerinden bir toplama genişletiyoruz:

\u003d (x 1, x 2, x 3, x 4) \u003d (-2a + 7b - 2, a, -2b + 1, b) \u003d (-2a, a, 0, 0) + (7b, 0, - 2b, b) + +(– 2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (– 2, 0, 1, 0 ).

f n = (- 2, 0, 1, 0), f o1 = (-2, 1, 0, 0), f o2 = (7, 0, -2, 1) elde ederiz.

Yorum. Homojen bir sistem için temel bir çözüm sistemi bulma sorunu benzer şekilde çözülür.

Alıştırma 3.1 Homojen bir sistemin temel çözüm sistemini bulun:

a)

b)

c) 2x 1 - x 2 + 3x 3 \u003d 0.

EGZERSİZ 3.2. Homojen olmayan sistemin belirli bir çözümünü ve ilgili homojen sistemin temel çözüm sistemini bulun:

a)

b)

Geometride bir vektör, yönlendirilmiş bir segment olarak anlaşılır ve paralel öteleme ile birbirinden elde edilen vektörler eşit kabul edilir. Tüm eşit vektörler aynı vektör olarak kabul edilir. Vektörün başlangıcı uzayda veya düzlemde herhangi bir noktaya yerleştirilebilir.

Vektörün uçlarının koordinatları uzayda verilirse: A(x 1 , y 1 , z 1), B(x 2 , y 2 , z 2), sonra

= (x 2 – x 1 , y 2 – y 1 , z 2 – z 1). (1)

Benzer bir formül düzlemde de geçerlidir. Bu, bir vektörün bir koordinat dizisi olarak yazılabileceği anlamına gelir. Vektörler üzerinde işlemler, - bir sayı ile toplama ve çarpma, diziler üzerinde bileşen bileşen yapılır. Bu, vektör kavramını herhangi bir sayı dizisi olarak anlayarak vektör kavramını genişletmeyi mümkün kılar. Örneğin, bir lineer denklem sisteminin çözümü ve ayrıca sistem değişkenlerinin herhangi bir değer kümesi bir vektör olarak kabul edilebilir.

Aynı uzunluktaki dizelerde toplama işlemi kurala göre yapılır.

(a 1 , 2 , … , bir n) + (b 1 , b 2 , … , b n) = (a 1 + b 1 , a 2 + b 2 , … , bir n+b n). (2)

Bir dizgenin bir sayı ile çarpımı kurala göre yapılır.

l(a 1 , 2 , … , bir n) = (la 1 , la 2 , … , la n). (3)

Verilen uzunlukta satır vektörleri kümesi n Belirtilen vektör toplama ve bir sayı ile çarpma işlemleriyle, adı verilen cebirsel bir yapı oluşturur. n-boyutlu lineer uzay.

Vektörlerin doğrusal bir kombinasyonu bir vektördür , burada λ 1 , ... , λ m keyfi katsayılardır.

En az bir sıfır olmayan katsayıya sahip olan, 'ye eşit doğrusal kombinasyonu varsa, bir vektör sistemine doğrusal bağımlı denir.

Bir vektör sistemi, lineer kombinasyonlarından herhangi birinde 'ye eşitse, tüm katsayıları sıfırsa, lineer bağımsız olarak adlandırılır.

Böylece, vektörler sisteminin doğrusal bağımlılığı sorununun çözümü, denklemin çözümüne indirgenir.

x 1 + x 2 + … + x m = . (4)

Bu denklemin sıfırdan farklı çözümleri varsa, vektörler sistemi lineer bağımlıdır. Sıfır çözüm benzersiz ise, vektörler sistemi lineer bağımsızdır.

(4) sistemini çözmek için, açıklık için, vektörler satırlar şeklinde değil, sütunlar şeklinde yazılabilir.

Ardından, sol tarafta dönüşümler gerçekleştirdikten sonra, denklem (4)'e eşdeğer bir lineer denklem sistemine ulaşıyoruz. Bu sistemin ana matrisi, sütunlar halinde düzenlenmiş orijinal vektörlerin koordinatlarından oluşur. Sistem homojen olduğu için burada serbest üyeler sütununa gerek yoktur.

temel vektörler sistemi (sonlu veya sonsuz, özellikle tüm doğrusal uzay), sistemin herhangi bir vektörünün ifade edilebildiği, boş olmayan, doğrusal olarak bağımsız alt sistemidir.

Örnek 1.5.2. Vektörler sisteminin temelini bulun = (1, 2, 2, 4), = (2, 3, 5, 1), = (3, 4, 8, –2), = (2, 5, 0, 3) ve diğer vektörleri bazında ifade eder.

Karar. Bu vektörlerin koordinatlarının sütunlar halinde düzenlendiği bir matris oluşturuyoruz. Bu sistemin matrisi x 1 + x 2 + x 3 + x 4 =. . Matrisi kademeli bir forma getiriyoruz:

~ ~ ~

Bu vektör sisteminin temeli, dairelerle işaretlenmiş satırların önde gelen öğelerine karşılık gelen vektörler tarafından oluşturulur. Vektörü ifade etmek için denklemi çözeriz x 1 + x 2 + x 4 = . Bu, matrisi orijinalden elde edilen doğrusal denklemler sistemine, karşılık gelen sütunu serbest terimler sütununun yerine yeniden düzenleyerek indirgenir. Bu nedenle, kademeli bir forma indirirken, matris üzerinde yukarıdaki gibi aynı dönüşümler yapılacaktır. Bu, elde edilen matrisi, içindeki sütunların gerekli permütasyonlarını yaparak kademeli bir biçimde kullanabileceğimiz anlamına gelir: daireli sütunlar dikey çubuğun soluna, vektöre karşılık gelen sütun sağa yerleştirilir. barın.

Art arda buluyoruz:

x 4 = 0;

x 2 = 2;

x 1 + 4 = 3, x 1 = –1;

Yorum. Birkaç vektörü temel üzerinden ifade etmek gerekirse, her biri için karşılık gelen doğrusal denklem sistemi oluşturulur. Bu sistemler sadece ücretsiz üyelerin sütunlarında farklılık gösterecektir. Bu durumda, her sistem diğerlerinden bağımsız olarak çözülür.

ALIŞTIRMA 1.4. Vektörler sisteminin temelini bulun ve vektörlerin geri kalanını taban cinsinden ifade edin:

a) = (1, 3, 2, 0), = (3, 4, 2, 1), = (1, –2, –2, 1), = (3, 5, 1, 2);

b) = (2, 1, 2, 3), = (1, 2, 2, 3), = (3, –1, 2, 2), = (4, –2, 2, 2);

c) = (1, 2, 3), = (2, 4, 3), = (3, 6, 6), = (4, –2, 1); = (2, -6, -2).

Belirli bir vektör sisteminde, bir baz genellikle farklı şekillerde ayırt edilebilir, ancak tüm bazlar aynı sayıda vektöre sahip olacaktır. Doğrusal bir uzay temelindeki vektörlerin sayısına uzayın boyutu denir. İçin n-boyutlu lineer uzay n uzayın boyutudur, çünkü bu uzayın standart bir temeli vardır = (1, 0, … , 0), = (0, 1, … , 0), … , = (0, 0, … , 1). Bu temelde, herhangi bir vektör = (a 1 , a 2 , … , a n) aşağıdaki gibi ifade edilir:

= (a 1 , 0, … , 0) + (0, a 2 , … , 0) + … + (0, 0, … , a n) =

A 1 (1, 0, … , 0) + bir 2 (0, 1, … , 0) + … + bir n(0, 0, ... ,1) = bir 1 + bir 2 + ... + bir n .

Böylece vektörün satırındaki bileşenler = (a 1 , a 2 , … , a n) standart baz açısından genişlemedeki katsayılarıdır.

Uçakta düz çizgiler

Analitik geometri problemi, koordinat yönteminin geometrik problemlere uygulanmasıdır. Böylece problem cebirsel bir forma çevrilir ve cebir vasıtasıyla çözülür.

Formun ifadesi isminde vektörlerin doğrusal kombinasyonu A 1 , A 2 ,...,Bir n katsayılarla λ 1, λ 2 ,...,λ n.

Bir vektör sisteminin lineer bağımlılığını belirleme

vektör sistemi A 1 , A 2 ,...,Bir n isminde lineer bağımlı, sıfır olmayan bir sayı kümesi varsa λ 1, λ 2 ,...,λ n, altında vektörlerin lineer kombinasyonu λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n sıfır vektörüne eşit, yani denklem sistemi: sıfır olmayan bir çözüme sahiptir.
sayı kümesi λ 1, λ 2 ,...,λ n sayılardan en az biri sıfır değilse λ 1, λ 2 ,...,λ n sıfırdan farklıdır.

Bir vektör sisteminin lineer bağımsızlığını belirleme

vektör sistemi A 1 , A 2 ,...,Bir n isminde Doğrusal bağımsız, eğer bu vektörlerin lineer kombinasyonu λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n sadece sıfır bir sayı kümesi için sıfır vektörüne eşittir λ 1, λ 2 ,...,λ n , yani denklem sistemi: A 1 x 1 +A 2 x 2 +...+A n x n =Θ benzersiz bir sıfır çözüme sahiptir.

Bir vektör sisteminin lineer bağımlı olup olmadığını kontrol edin

Karar:

1. Bir denklem sistemi oluşturuyoruz:

2. Gauss yöntemini kullanarak çözüyoruz. Sistemin Ürdün dönüşümleri Tablo 29.1'de verilmiştir. Hesaplanırken sistemin doğru kısımları sıfıra eşit olduğundan ve Jordan dönüşümleri altında değişmediğinden yazılmaz.

3. Tablonun son üç satırından izin verilen sistemi orijinaline eşdeğer yazıyoruz sistem:

4. Sistemin genel çözümünü alıyoruz:

5. Serbest değişken x 3 =1'in değerini kendi takdirinize göre belirledikten sonra, sıfır olmayan belirli bir çözüm elde ederiz X=(-3,2,1).

Cevap: Böylece, sıfır olmayan bir sayı kümesiyle (-3,2,1), vektörlerin doğrusal kombinasyonu sıfır vektörü -3A 1 +2A 2 +1A 3 =Θ'ye eşittir. Buradan, lineer bağımlı vektörler sistemi.

Vektör sistemlerinin özellikleri

Mülk (1)
Vektörler sistemi doğrusal olarak bağımlıysa, o zaman vektörlerden en az biri geri kalanında ayrıştırılabilir ve bunun tersi, sistemin vektörlerinden en az biri geri kalanında ayrıştırılırsa, vektörler sistemi doğrusal olarak bağımlıdır. .

Mülk (2)
Vektörlerin herhangi bir alt sistemi doğrusal olarak bağımlıysa, tüm sistem doğrusal olarak bağımlıdır.

Mülk (3)
Bir vektör sistemi lineer olarak bağımsızsa, alt sistemlerinden herhangi biri lineer olarak bağımsızdır.

Mülk (4)
Sıfır vektör içeren herhangi bir vektör sistemi lineer olarak bağımlıdır.

Mülk (5)
Bir m boyutlu vektörler sistemi, vektörlerin sayısı n boyutlarından büyükse (n>m) her zaman doğrusal olarak bağımlıdır.

Vektör sisteminin temeli

Vektörler sisteminin temeli A 1 , A 2 ,..., A n böyle bir alt sistemdir B 1 , B 2 ,...,B r(B 1 ,B 2 ,...,B r vektörlerinin her biri, aşağıdaki koşulları sağlayan A 1 , A 2 ,..., A n vektörlerinden biridir):
1. B 1 ,B 2 ,...,B r lineer bağımsız vektör sistemi;
2. herhangi bir vektör bir j A 1 , A 2 ,..., A n sisteminin B 1 ,B 2 ,...,B r vektörleri cinsinden doğrusal olarak ifade edilir

r tabana dahil edilen vektörlerin sayısıdır.

Teorem 29.1 Bir vektör sisteminin birim bazında.

Bir m boyutlu vektörler sistemi m farklı E 1 E 2 ,..., E m birim vektörü içeriyorsa, bunlar sistemin temelini oluşturur.

Bir vektörler sisteminin temelini bulmak için algoritma

A 1 ,A 2 ,...,A n vektörlerinin sisteminin temelini bulmak için aşağıdakiler gereklidir:

• Vektörler sistemine karşılık gelen homojen bir denklem sistemi oluşturun A 1 x 1 +A 2 x 2 +...+A n x n =Θ
• bu sistemi getir

Temelde yer almayan vektörler ve vektörler sisteminin temelini bulun, temelde genişletin:

a 1 = {5, 2, -3, 1}, a 2 = {4, 1, -2, 3}, a 3 = {1, 1, -1, -2}, a 4 = {3, 4, -1, 2}, a 5 = {13, 8, -7, 4}.

Karar. Homojen bir lineer denklem sistemi düşünün

a 1 X 1 + a 2 X 2 + a 3 X 3 + a 4 X 4 + a 5 X 5 = 0

veya genişletildi.

Bu sistemi Gauss yöntemini kullanarak, satırları ve sütunları değiştirmeden ve ayrıca ana öğeyi sol üst köşede değil, satır boyunca seçmeden çözeceğiz. Görev dönüştürülmüş vektör sisteminin köşegen kısmını seçin.

~ ~

~ ~ ~ .

Orijinaline eşdeğer izin verilen vektör sistemi şu şekildedir:

a 1 1 X 1 + a 2 1 X 2 + a 3 1 X 3 + a 4 1 X 4 + a 5 1 X 5 = 0 ,

nerede a 1 1 = , a 2 1 = , a 3 1 = , a 4 1 = , a 5 1 = . (1)

vektörler a 1 1 , a 3 1 , a 4 1 köşegen bir sistem oluşturur. Bu nedenle vektörler a 1 , a 3 , a 4 vektörler sisteminin temelini oluşturur a 1 , a 2 , a 3 , a 4 , a 5 .

Şimdi vektörleri genişletiyoruz a 2 ve a 5 temelinde a 1 , a 3 , a 4. Bunu yapmak için önce karşılık gelen vektörleri genişletiriz. a 2 1 ve a 5 1 diyagonal sistem a 1 1 , a 3 1 , a 4 1 , köşegen sistemdeki vektör açılımının katsayılarının onun koordinatları olduğunu akılda tutarak x ben.

(1)'den elimizde:

a 2 1 = a 3 1 (-1) + a 4 1 0 + a 1 1 1 a 2 1 = a 1 1 – a 3 1 .

a 5 1 = a 3 1 0 + a 4 1 1+ a 1 1 2 a 5 1 = 2a 1 1 + a 4 1 .

vektörler a 2 ve a 5 temelde genişletmek a 1 , a 3 , a 4 vektörlerle aynı katsayılara sahip a 2 1 ve a 5 1 diyagonal sistem a 1 1 , a 3 1 , a 4 1 (bu katsayılar x ben). Buradan,

a 2 = a 1 – a 3 , a 5 = 2a 1 + a 4 .

Görevler. 1.Vektörler sisteminin temelini ve tabana dahil olmayan vektörleri bulun, tabana göre genişletin:

1. a 1 = { 1, 2, 1 }, a 2 = { 2, 1, 3 }, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4 }.

2. a 1 = { 1, 1, 2 }, a 2 = { 0, 1, 2 }, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0 }.

3. a 1 = { 1, -2, 3 }, a 2 = { 0, 1, -1 }, a 3 = { 1, 3, 0 }, a 4 = { 0, -7, 3 }, a 5 = { 1, 1, 1 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

2. Bir vektör sisteminin tüm tabanlarını bulun:

1. a 1 = { 1, 1, 2 }, a 2 = { 3, 1, 2 }, a 3 = { 1, 2, 1 }, a 4 = { 2, 1, 2 }.

2. a 1 = { 1, 1, 1 }, a 2 = { -3, -5, 5 }, a 3 = { 3, 4, -1 }, a 4 = { 1, -1, 4 }.