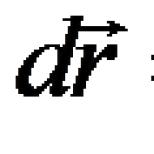3 değişkenin kısmi türevleri. Birinci dereceden kısmi türevler. tam diferansiyel. Benzer şekilde, y'ye göre z'nin kısmi bir artışı elde ederiz.

İki değişkenli fonksiyonlar, kısmi türevler, diferansiyeller ve gradyan

Konu 5.İki değişkenli fonksiyonlar.

kısmi türevler

İki değişkenli bir fonksiyonun tanımı, ayar yolları.

Özel türevler.

Bir değişkenin gradyan işlevi

Kapalı bir sınırlı alanda iki değişkenli bir fonksiyonun en büyük ve en küçük değerlerini bulma

1. Birkaç değişkenli bir fonksiyonun tanımı, ayar yolları

İçin iki değişkenli fonksiyonlar
tanım alanı biraz bir uçaktaki noktalar kümesi
, ve aralık eksendeki boşluktur
.

Görsel temsil için iki değişkenli fonksiyonlar nyh uygula seviye çizgileri.

Misal . fonksiyon için
bir grafik ve seviye çizgileri oluşturun. Bir noktadan geçen düz bir doğrunun denklemini yazın
.

Doğrusal fonksiyon grafiği bir uçak boşlukta.

Bir fonksiyon için grafik, noktalardan geçen bir düzlemdir.
,
,
.

Fonksiyon seviye çizgileri denklemi olan paralel çizgilerdir
.

İçin iki değişkenli doğrusal fonksiyon
seviye çizgileri denklem tarafından verilir
ve temsil etmek düzlemde paralel çizgiler ailesi.

Fonksiyon Grafiği 0 1 2 X

Özellik düzeyi çizgileri

özel profesyoneliki değişkenli türev fonksiyonları

işlevi düşünün
. bir değişken verelim noktada
keyfi artış
, ayrılmak değişken değer değişmemiş. Karşılık gelen fonksiyon artışı

isminde değişken tarafından bir fonksiyonun kısmi artışı noktada
.

Benzer şekilde tanımlanmış bir fonksiyonun kısmi artışıdeğişkene göre: .

atamagöre kısmi türev: , ,
,
.

Bir fonksiyonun bir değişkene göre kısmi türevi limit denir :

Tanımlamalar: , ,
,
.

Kısmi türevi bulmak için
bir değişkenle ilgili olarak, bir değişkenin bir fonksiyonunun türevini alma kuralları kullanılır, değişkenin sabit olduğunu varsayarsak.

Benzer şekilde, bir değişkene göre kısmi türevi bulmak için değişken sabit kabul edilir .

Misal . fonksiyon için
kısmi türevleri bul
,
ve değerlerini bir noktada hesaplayın
.

Bir fonksiyonun kısmi türevi
değişkene göre sabit olduğu varsayımı altındadır:

Sabit olduğunu varsayarak fonksiyonun 'ye göre kısmi türevini bulun:

Kısmi türevlerin değerlerini hesaplayalım
,
:

;
.

İkinci dereceden kısmi türevler birkaç değişkenli fonksiyonlara birinci dereceden kısmi türevlerin kısmi türevleri denir.

Fonksiyonun 2. mertebesinin kısmi türevlerini yazalım:

;
;

;
.

;
vb.

Birkaç değişkenli bir fonksiyonun karışık kısmi türevleri bir noktada sürekli ise
, sonra onlar birbirine eşit Bu noktada. Bu nedenle, iki değişkenli bir fonksiyon için, karışık kısmi türevlerin değerleri, türev sırasına bağlı değildir:

Misal. Bir fonksiyon için ikinci dereceden kısmi türevleri bulun
ve
.

Karar

Karışık kısmi türev, fonksiyonun ilk olarak ardışık türevlenmesiyle bulunur. (sabit varsayılarak) ile ilgili olarak, sonra türevin türevini almak
tarafından (sabit varsayılarak).

Türev, önce fonksiyonun 'ye göre türevini, ardından türevin 'ye göre türevini alarak bulunur.

Karışık kısmi türevler birbirine eşittir:
.

3. İki değişkenli bir fonksiyonun gradyanı

gradyan özellikleri

Misal . Verilen bir fonksiyon
. Gradyan Bul
noktada
ve inşa et.

Karar

Gradyanın koordinatlarını bulun - kısmi türevler.

Noktada
gradyan eşittir . vektör başlangıç
noktada ve noktada sona erer.

4. Kapalı sınırlı bir bölgede iki değişkenli bir fonksiyonun en büyük ve en küçük değerlerini bulma

Sorunun formülasyonu. Düzlemde kapalı bir sınırlı alan bırakın
biçimindeki bir eşitsizlik sistemi tarafından verilir
. Fonksiyonun en büyük ve en küçük değerleri aldığı bölgedeki noktaların bulunması gerekir.

Önemli ekstremum sorunu, matematiksel modeli şunları içerir: doğrusal kısıtlamalar (denklemler, eşitsizlikler) ve doğrusal işlev
.

Sorunun formülasyonu. Bir fonksiyonun en büyük ve en küçük değerlerini bulun
(2.1)

kısıtlamalar altında

(2.2)

. (2.3)

Çok değişkenli doğrusal bir fonksiyon için kritik noktalar olmadığından içeri alanlar
, o zaman bir ekstremum ile amaç fonksiyonunu sağlayan optimal çözüm sadece elde edilir. bölgenin kenarında. Doğrusal kısıtlamalarla tanımlanan alan için olası uç noktalar şunlardır: köşe noktaları. Bu, sorunun çözümünü düşünmemizi sağlar grafik yöntemi.

Doğrusal eşitsizlikler sisteminin grafik çözümü

Bu problemi grafiksel olarak çözmek için, iki değişkenli doğrusal eşitsizlik sistemlerini grafiksel olarak çözebilmek gerekir.

Prosedür:

eşitsizliğine dikkat
tanımlar sağ koordinat yarım düzlem(eksenden
) ve eşitsizlik
- üst koordinat yarım düzlemi(eksenden
).

Misal. Grafiksel eşitsizliği çözün
.

Sınır çizgisinin denklemini yazıyoruz
ve onu iki noktadan inşa edin, örneğin,
ve
. Düz bir çizgi, bir düzlemi iki yarım düzleme böler.

nokta koordinatları
eşitsizliği sağlamak (
doğrudur), bu noktayı içeren yarım düzlemin tüm noktalarının koordinatlarının eşitsizliği sağladığı anlamına gelir. Eşitsizliğin çözümü, sınırdaki noktalar da dahil olmak üzere sınır çizgisinin sağında bulunan yarım düzlemin noktalarının koordinatları olacaktır. İstenen yarım düzlem şekilde vurgulanmıştır.

Karar
eşitsizlik sistemi denir kabul edilebilir, koordinatları negatif değilse , . Eşitsizlikler sistemine kabul edilebilir çözümler kümesi, koordinat düzleminin ilk çeyreğinde yer alan bir alan oluşturur.

Misal. Eşitsizlikler sisteminin çözüm alanını oluşturunuz.

Eşitsizliklerin çözümleri:

1)
- düz çizgiye göre solda ve aşağıda bulunan yarım düzlem ( )
;

2)
düz çizgiye göre sağ-alt yarım düzlemde bulunan bir yarım düzlemdir ( )
;

3)
- düz çizginin sağında bulunan yarım düzlem ( )
;

4) - apsis ekseninin üzerinde yarım düzlem, yani düz bir çizgi ( )
.

Kabul edilebilir çözümlerin alanı Verilen lineer eşitsizlikler sistemi, dörtgenin içinde ve sınırında bulunan noktalar kümesidir.
, hangisi kavşak dört yarım uçak.

Doğrusal bir fonksiyonun geometrik gösterimi

(düzey çizgileri ve gradyan)

değeri düzeltelim
, denklemi elde ederiz
, geometrik olarak düz bir çizgiyi tanımlar. Her noktada, doğrudan fonksiyon değeri alır. ve bir seviye çizgisi. vermek çeşitli değerler, örneğin,

, ... , bir dizi seviye çizgisi elde ederiz - paralel küme doğrudan.

Hadi yapalım gradyan- vektör
koordinatları fonksiyondaki değişkenlerin katsayılarının değerlerine eşit olan
. Bu vektör: 1) her düz çizgiye dik (düz çizgi)
; 2) amaç fonksiyonunun artış yönünü gösterir.

Misal . Çizim Düzeyi Çizgileri ve Özellik Gradyanı
.

, , noktasındaki seviye çizgileri düzdür

,
,

, birbirine paralel. Gradyan, her seviye çizgisine dik bir vektördür.

Bir bölgedeki doğrusal bir fonksiyonun en büyük ve en küçük değerlerinin grafiksel olarak bulunması

Problemin geometrik ifadesi. Doğrusal eşitsizlikler sisteminin çözüm alanında, iki değişkenli doğrusal bir fonksiyonun en büyük (en küçük) değerine karşılık gelen, seviye çizgisinin geçtiği noktayı bulun.

sıralama:

4. A noktasında kesişen doğruların denklem sistemini çözerek A noktasının koordinatlarını bulun ve fonksiyonun en küçük değerini hesaplayın.
. Benzer şekilde - B noktası ve fonksiyonun en büyük değeri için
. point.variables üzerine kurulu Özeltürevlerfonksiyonlar birçok değişkenler ve farklılaşma tekniği. aşırı fonksiyonlarikideğişkenler ve onun gerekli...

Her kısmi türev (üzerinde x ve tarafından y) iki değişkenli bir fonksiyonun, bir değişkenin fonksiyonunun diğer değişkenin sabit değerine sahip adi türevidir:

(nerede y= sabit),

(nerede x= sabit).

Bu nedenle, kısmi türevler şu şekilde hesaplanır: tek değişkenli fonksiyonların türevlerini hesaplamak için formüller ve kurallar, diğer değişkeni sabit (sabit) olarak kabul ederken.

Örneklerin analizine ve bunun için gerekli minimum teoriye ihtiyacınız yoksa, ancak yalnızca sorununuza bir çözüme ihtiyacınız varsa, o zaman devam edin. çevrimiçi kısmi türev hesaplayıcı .

Sabitin fonksiyonda nerede olduğunu takip etmeye odaklanmak zorsa, sabit değerli bir değişken yerine örneğin taslak çözümünde herhangi bir sayıyı değiştirebilirsiniz - o zaman kısmi türevi normal olarak hızlı bir şekilde hesaplayabilirsiniz. tek değişkenli bir fonksiyonun türevi. Bitirirken sadece sabiti (sabit değerli bir değişken) yerine döndürmeyi unutmamak gerekir.

Kısmi türevlerin yukarıda açıklanan özelliği, sınav sorularında bulunabilen kısmi türev tanımından kaynaklanmaktadır. Bu nedenle, aşağıdaki tanımla tanışmak için teorik referansı açabilirsiniz.

Bir fonksiyonun sürekliliği kavramı z= f(x, y) bir noktada bu kavrama benzer şekilde tek değişkenli bir fonksiyon için tanımlanır.

İşlev z = f(x, y) ise bir noktada sürekli olarak adlandırılır.

Fark (2), fonksiyonun toplam artışı olarak adlandırılır. z(her iki argüman da artırılarak elde edilir).

fonksiyon olsun z= f(x, y) ve nokta

fonksiyon değişirse z bağımsız değişkenlerden yalnızca biri değiştiğinde oluşur, örneğin, x, diğer argümanın sabit bir değeri ile y, sonra fonksiyon artırılacaktır

fonksiyonun kısmi artışı denir f(x, y) üzerinde x.

Fonksiyon değişikliği göz önüne alındığında z argümanlardan sadece birinin değişmesine bağlı olarak, aslında tek değişkenli bir fonksiyona geçiyoruz.

Sonlu bir sınır varsa

o zaman fonksiyonun kısmi türevi denir f(x, y) argümanla x ve sembollerden biri ile gösterilir

(4)

Kısmi artış benzer şekilde tanımlanır züzerinde y:

ve kısmi türev f(x, y) üzerinde y:

(6)

örnek 1

Karar. "x" değişkenine göre kısmi türevi buluyoruz:

(y sabit);

"y" değişkenine göre kısmi türevi buluyoruz:

(x sabit).

Gördüğünüz gibi, değişkenin ne ölçüde sabit olduğu önemli değil: bu durumda, kısmisini bulduğumuz değişkenle birlikte bir faktör olan (olağan türev durumunda olduğu gibi) sadece bir sayıdır. türev. Sabit değişken, kendisine göre kısmi türevi bulduğumuz değişkenle çarpılmazsa, bu yalnız sabit, adi türev durumunda olduğu gibi, ne dereceye kadar olursa olsun, yok olur.

Örnek 2 Verilen bir fonksiyon

Kısmi Türevleri Bul

(x ile) ve (y ile) ve noktadaki değerlerini hesaplayın ANCAK (1; 2).

Karar. sabit y birinci terimin türevi, güç fonksiyonunun türevi olarak bulunur ( bir değişkenin türev fonksiyonları tablosu):

sabit x birinci terimin türevi, üstel fonksiyonun türevi ve ikincisi - sabitin türevi olarak bulunur:

Şimdi noktada bu kısmi türevlerin değerlerini hesaplıyoruz. ANCAK (1; 2):

Kısmi türevlerle ilgili problemlerin çözümünü şuradan kontrol edebilirsiniz: çevrimiçi kısmi türev hesaplayıcı .

Örnek 3 Fonksiyonların Kısmi Türevlerini Bulun

Karar. Bir adımda buluyoruz

(y x, sinüs argümanı 5'miş gibi x: aynı şekilde, fonksiyonun işaretinden önce 5 görünür);

(x sabittir ve bu durumda bir faktördür y).

Kısmi türevlerle ilgili problemlerin çözümünü şuradan kontrol edebilirsiniz: çevrimiçi kısmi türev hesaplayıcı .

Üç veya daha fazla değişkenli bir fonksiyonun kısmi türevleri benzer şekilde tanımlanır.

Her bir değer kümesi ise ( x; y; ...; t) kümeden bağımsız değişkenler D belirli bir değere karşılık gelir sen birçoktan E, o zamanlar sen değişkenlerin bir fonksiyonu denir x, y, ..., t ve belirtmek sen= f(x, y, ..., t).

Üç veya daha fazla değişkenli fonksiyonlar için geometrik yorum yoktur.

Birkaç değişkenli bir fonksiyonun kısmi türevleri de bağımsız değişkenlerden sadece birinin değiştiği, diğerlerinin sabit olduğu varsayımı altında tanımlanır ve hesaplanır.

Örnek 4 Fonksiyonların Kısmi Türevlerini Bulun

Karar. y ve z sabit:

x ve z sabit:

x ve y sabit:

Kısmi türevleri kendi başınıza bulun ve ardından çözümlere bakın

Örnek 5

Örnek 6 Bir fonksiyonun kısmi türevlerini bulun.

Birkaç değişkenli bir fonksiyonun kısmi türevi aynı tek değişkenli bir fonksiyonun türevi olarak mekanik anlam, işlevin bağımsız değişkenlerden birindeki değişikliğe göre değişme hızıdır.

Örnek 8 akış miktarı P demiryolu yolcuları bir fonksiyon olarak ifade edilebilir

nerede P- yolcu sayısı, N- ilgili noktaların sakinlerinin sayısı, R– noktalar arasındaki mesafe.

Bir fonksiyonun kısmi türevi Püzerinde R eşittir

yolcu akışındaki azalmanın, noktalarda aynı sayıda sakin için karşılık gelen noktalar arasındaki mesafenin karesiyle ters orantılı olduğunu göstermektedir.

Kısmi türev Püzerinde N eşittir

yolcu akışındaki artışın, noktalar arasındaki mesafeleri aynı olan yerleşim yerlerinin sakinlerinin sayısının iki katı ile orantılı olduğunu göstermektedir.

Kısmi türevlerle ilgili problemlerin çözümünü şuradan kontrol edebilirsiniz: çevrimiçi kısmi türev hesaplayıcı .

Tam diferansiyel

Kısmi türevin ve karşılık gelen bağımsız değişkenin artışının çarpımına kısmi diferansiyel denir. Kısmi diferansiyeller aşağıdaki gibi gösterilir:

Tüm bağımsız değişkenler üzerindeki kısmi diferansiyellerin toplamı, toplam diferansiyeli verir. İki bağımsız değişkenli bir fonksiyon için, toplam diferansiyel eşitlik ile ifade edilir.

(7)

Örnek 9 Bir fonksiyonun tam diferansiyelini bulun

Karar. Formül (7) kullanmanın sonucu:

Bir tanım kümesinin her noktasında toplam diferansiyeli olan bir fonksiyona, o tanım kümesinde türevlenebilir denir.

Toplam farkı kendi başınıza bulun ve ardından çözümü görün

Tıpkı tek değişkenli bir fonksiyon durumunda olduğu gibi, belirli bir bölgedeki bir fonksiyonun türevlenebilirliği, bu bölgede sürekliliğini ima eder, ancak bunun tersi olmaz.

Bir fonksiyonun türevlenebilirliği için kanıt olmadan yeterli bir koşul formüle edelim.

Teorem. eğer fonksiyon z= f(x, y) sürekli kısmi türevleri vardır

belirli bir bölgede, o zaman bu bölgede türevlenebilir ve diferansiyeli formül (7) ile ifade edilir.

Bir değişkenli bir fonksiyon durumunda olduğu gibi, fonksiyonun diferansiyeli, fonksiyonun artışının ana lineer kısmıdır, bu nedenle, birkaç değişkenli bir fonksiyon durumunda, toplam diferansiyelin şu şekilde olduğu gösterilebilir. ana, bağımsız değişkenlerin artışlarına göre doğrusal, fonksiyonun toplam artışının bir parçası.

İki değişkenli bir fonksiyon için, fonksiyonun toplam artışı şu şekildedir:

(8)

burada α ve β ve için sonsuz küçüktür.

Daha yüksek siparişlerin kısmi türevleri

Kısmi türevler ve fonksiyonlar f(x, y) kendileri aynı değişkenlerin bazı fonksiyonlarıdır ve sırayla, daha yüksek dereceli kısmi türevler olarak adlandırılan farklı değişkenlere göre türevleri olabilir.

Tanım 1.11İki değişkenli bir fonksiyon verilsin z=z(x,y), (x,y)D . Nokta M 0 (x 0 ;y 0 ) - alanın iç noktası D .

eğer D öyle bir mahalle var ki UM 0 puan M 0 , hangi tüm noktalar için

sonra nokta M 0 yerel maksimum nokta denir. Ama anlamın kendisi z(M 0 ) - yerel maksimum.

Ama eğer tüm noktalar için

sonra nokta M 0 fonksiyonun yerel minimum noktası denir z(x,y) . Ama anlamın kendisi z(M 0 ) - yerel minimum.

Yerel maksimum ve yerel minimum, fonksiyonun yerel ekstremleri olarak adlandırılır. z(x,y) . Şek. 1.4 yerel maksimumun geometrik anlamını açıklar: M 0 yüzeyde olduğundan maksimum noktadır z=z(x,y) karşılık gelen noktası C 0 herhangi bir komşu noktanın üstünde C (bu, maksimumun yerelliğidir).

Yüzeyde bir bütün olarak noktalar olduğuna dikkat edin (örneğin, AT ) yukarıdakiler C 0 , ancak bu noktalar (örneğin, AT ) işaret etmek için "bitişik" değil C 0 .

Özellikle, nokta AT küresel maksimum kavramına karşılık gelir:

Küresel minimum benzer şekilde tanımlanır:

Global maksimum ve minimumların bulunması Bölüm 1.10'da tartışılacaktır.

Teorem 1.3(gerekli ekstremum koşullar).

fonksiyon olsun z =z(x,y),(x,y)D . Nokta M 0 (x 0 ;y 0 D - yerel ekstremum noktası.

Bu noktada varsa z" x ve z" y , o zamanlar

Geometrik kanıt "açıktır". noktada ise C 0 teğet bir düzlem çizmek için (Şekil 1.4), o zaman "doğal olarak" yatay olarak, yani. bir açıyla 0° eksene ey ve eksene kuruluş birimi .

Ardından kısmi türevlerin geometrik anlamlarına göre (Şekil 1.3):

hangi kanıtlanacaktı.

Tanım 1.12.

noktada ise M 0 (1.41) koşulları sağlandığında, fonksiyonun durağan noktası olarak adlandırılır. z(x,y) .

Teorem 1.4(bir ekstremum için yeterli koşullar).

İzin vermek z =z(x,y),(x,y)D noktanın bazı komşuluklarında ikinci dereceden kısmi türevleri olan M 0 (x 0 ,y 0 )D . Ve M 0 - durağan nokta (yani, gerekli koşullar (1.41) karşılanmıştır). Hesaplayalım:

Teoremin ispatı, bu öğreticide ele alınmayan konuları (birkaç değişkenli fonksiyonlar için Taylor formülü ve ikinci dereceden formlar teorisi) kullanır.

Örnek 1.13.

En uç noktayı keşfedin:

Karar

1. Sistemi (1.41) çözerek durağan noktaları bulun:

yani dört durağan nokta bulunur. 2.

Teorem 1.4'e göre bir noktada minimumdur. Ve

noktasında Teorem 1.4 ile

Maksimum. Ve

Ve hiçbir şey aramanıza gerek yok: ayrı makalemizde, yapabilmeniz için zaten her şeyi hazırladık. Şimdi kısmi türevlerden bahsedelim.

Faydalı haber bültenleri ve güncel öğrenci haberleri için telegram kanalımıza hoş geldiniz.

İki veya daha fazla değişkenin işlevi

Kısmi türevlerden bahsetmeden önce, onsuz kısmi türevin anlamı olmayan birkaç değişkenli fonksiyon kavramına değinmemiz gerekiyor. Okulda, tek değişkenli fonksiyonlarla uğraşmaya alışkınız:

Bu tür fonksiyonların türevlerini daha önce ele almıştık. Bir değişkenin fonksiyonunun grafiği, bir düzlemdeki bir çizgidir: düz bir çizgi, bir parabol, bir hiperbol, vb.

Ya başka bir değişken eklersek? Bunun gibi bir işlev elde edersiniz:

Bu, iki bağımsız değişkenin bir fonksiyonudur. x ve y. Böyle bir fonksiyonun grafiği, üç boyutlu uzayda bir yüzeydir: bir küre, bir hiperboloid, bir paraboloid veya bir boşlukta başka bir küresel at. Kısmi türev fonksiyonları z sırasıyla x ve y için aşağıdaki gibi yazılır:

Üç veya daha fazla değişkenli fonksiyonlar da vardır. Doğru, böyle bir fonksiyonun grafiğini çizmek imkansızdır: bu, tasvir edilemeyen en az dört boyutlu alan gerektirir.

Birinci dereceden kısmi türev

Ana kuralı hatırla:

Değişkenlerden birine göre kısmi türev hesaplanırken ikinci değişken sabit olarak alınır. Aksi takdirde, türevi hesaplama kuralları değişmez.

Yani kısmi türev esasen normal olandan farklı değildir. Bu nedenle, temel fonksiyonların türevleri tablosunu ve sıradan türevleri hesaplama kurallarını gözünüzün önünde bulundurun. Bunu oldukça açık hale getirmek için bir örneğe bakalım. Aşağıdaki fonksiyonun birinci mertebeden kısmi türevlerini hesaplamak istediğinizi varsayalım:

İlk olarak, y'yi adi bir sayı olarak kabul ederek, x'e göre kısmi türevi alıyoruz:

Şimdi x'i sabit alarak y'ye göre kısmi türevi ele alalım:

Gördüğünüz gibi, bu konuda karmaşık bir şey yok ve daha karmaşık örneklerle başarı sadece bir uygulama meselesidir.

İkinci dereceden kısmi türev

İkinci mertebeden kısmi türev nedir? Tıpkı ilki gibi. İkinci mertebeden kısmi türevleri bulmak için, sadece birinci mertebeden türevin türevini almanız yeterlidir. Yukarıdaki örneğe dönelim ve ikinci mertebeden kısmi türevleri hesaplayalım.

Oyuna göre:

Üçüncü ve daha yüksek derecelerin kısmi türevleri, hesaplama ilkesinde farklılık göstermez. Kuralları düzenleyelim:

Bir bağımsız değişkene göre türev alırken, ikincisi sabit olarak alınır.
İkinci mertebeden türev, birinci mertebeden türevin türevidir. Üçüncü mertebe, ikinci mertebeden türevin türevidir, vb.

Bir fonksiyonun kısmi türevleri ve toplam diferansiyeli

Pratik görevlerde sıkça sorulan bir soru, bir fonksiyonun toplam diferansiyelini bulmaktır. Birkaç değişkenli bir fonksiyon için, toplam diferansiyel, argümanların artışlarına göre fonksiyonun küçük toplam artışının ana doğrusal kısmı olarak tanımlanır.

Tanım kulağa hantal geliyor, ancak harflerle her şey daha kolay. Birkaç değişkenli bir fonksiyonun toplam birinci mertebeden diferansiyeli şuna benzer:

Kısmi türevlerin nasıl hesaplandığını bilerek, toplam diferansiyelin hesaplanmasında sorun yoktur.

Kısmi türevler o kadar da gereksiz bir konu değildir. Örneğin, ikinci mertebeden kısmi diferansiyel denklemler, gerçek fiziksel süreçlerin matematiksel tanımı için yaygın olarak kullanılmaktadır.

Burada birinci ve ikinci mertebeden kısmi türevlerin sadece genel, yüzeysel bir fikrini verdik. Bu konuyla ilgileniyor musunuz veya özel sorularınız mı var? Yorumlarda onlara sorun ve çalışmalarınızda nitelikli ve hızlı yardım için profesyonel öğrenci servisinin uzmanlarıyla iletişime geçin. Bizimle sorunla yalnız kalmayacaksınız!

Üç değişkenli bir fonksiyonun ikinci dereceden kısmi türevlerini bulmanın genel ilkesi, iki değişkenli bir fonksiyonun ikinci dereceden kısmi türevlerini bulma ilkesine benzer.

İkinci mertebeden kısmi türevleri bulmak için önce birinci mertebeden kısmi türevleri bulmalısınız veya başka bir gösterimde:

İkinci mertebeden dokuz kısmi türev vardır.

Birinci grup, aynı değişkenlere göre ikinci türevlerdir:

Veya - "x"e göre ikinci türev;

Veya - "y"ye göre ikinci türev;

Veya - "z"ye göre ikinci türev.

İkinci grup ise karışık 2. dereceden kısmi türevler, bunlardan altı tane var:

Veya - karışık"x y'ye göre" türevi;

Veya - karışık"y x'e göre" türevi;

Veya - karışık"x z'ye göre" türevi;

Veya - karışık"po zet x" türevi;

Veya - karışık"Z oyununa göre" türevi;

Veya - karışık türevi "po z y".

İki değişkenli bir fonksiyon durumunda olduğu gibi, problem çözerken, ikinci dereceden karışık türevlerin aşağıdaki eşitliklerine odaklanılabilir:

Not: Açıkçası, bu her zaman böyle değildir. Karışık türevlerin eşitliği için süreklilik şartının yerine getirilmesi gerekmektedir.

Her ihtimale karşı, bu rezaletin yüksek sesle nasıl okunacağına dair birkaç örnek:

- "y'de iki kez iki vuruş";

- “de iki y po de zet meydanı”;

- “z üzerinde x üzerinde iki vuruş”;

- "iki y po de z po de y".

Örnek 10

Üç değişkenli bir fonksiyon için tüm birinci ve ikinci mertebeden kısmi türevleri bulun:

Karar:İlk olarak, birinci dereceden kısmi türevleri buluyoruz:

Bulunan türevi alıyoruz

ve "y" ile ayırt edin:

Bulunan türevi alıyoruz

ve onu "x" ile ayırt edin:

Eşitlik yapılır. İyi.

İkinci karışık türev çifti ile ilgileniyoruz.

Bulunan türevi alıyoruz

ve "z" ile ayırt edin:

Bulunan türevi alıyoruz

ve onu "x" ile ayırt edin:

Eşitlik yapılır. İyi.

Benzer şekilde, üçüncü karışık türev çifti ile ilgileniyoruz:

Eşitlik yapılır. İyi.

Yapılan çalışmadan sonra, birinci mertebeden tüm kısmi türevleri doğru bir şekilde bulduğumuz ve ikinci olarak 2. mertebeden karışık kısmi türevleri de doğru bir şekilde bulduğumuz garanti edilebilir.

İkinci mertebeden üç kısmi türev daha bulmak için kalır, burada hatalardan kaçınmak için mümkün olduğunca konsantre olmalısınız:

Hazır. Yine, görev hacimli olduğu kadar zor değil. Çözüm kısaltılabilir ve karışık kısmi türevlerin eşitlikleri olarak adlandırılabilir, ancak bu durumda doğrulama yapılmayacaktır. Bu yüzden zaman ayırıp bulmak daha iyi Tümü türevler (ayrıca, bu öğretmen tarafından istenebilir) veya aşırı durumlarda bir taslağı kontrol edin.

Örnek 11

Üç değişkenli bir fonksiyon için tüm birinci ve ikinci mertebeden kısmi türevleri bulun

Bu bir kendin yap örneğidir.

Çözümler ve cevaplar:

Örnek 2:Karar:

Örnek 4:Karar: Birinci mertebeden kısmi türevleri bulalım.

Birinci mertebenin toplam diferansiyelini oluşturuyoruz:

Örnek 6:Karar: M(1, -1, 0):

Örnek 7:Karar: noktasında birinci mertebeden kısmi türevleri hesaplayalım.M(1, 1, 1):

Örnek 9:Karar:

Örnek 11:Karar: Birinci mertebeden kısmi türevleri bulalım:

İkinci mertebeden kısmi türevleri bulalım:

integraller

8.1. Belirsiz integral. Detaylı Çözüm Örnekleri

konuyu incelemeye başlayalım Belirsiz integral" ve ayrıca en basit (ve tam olarak değil) integrallerin çözüm örneklerini ayrıntılı olarak analiz edin. Her zamanki gibi, kendimizi sayısız ders kitabında bulunan minimum teori ile sınırlayacağız, görevimiz integrallerin nasıl çözüleceğini öğrenmek.

Malzemede başarılı bir şekilde ustalaşmak için bilmeniz gerekenler nelerdir? İntegral hesabı ile başa çıkabilmek için, en azından ortalama düzeyde türevleri bulabilmeniz gerekir. Arkanızda birkaç düzine veya daha iyisi, bağımsız olarak bulunan yüzlerce türeviniz varsa, bu gereksiz bir deneyim olmayacaktır. En azından, en basit ve en yaygın işlevleri ayırt etme görevi sizi şaşırtmamalıdır.

Görünüşe göre, makaledeki integrallerden bahsediyorsak, türevler nerede ?! Ve işte olay. Gerçek şu ki, türev bulma ve belirsiz integral bulma (farklılaşma ve entegrasyon), toplama/çıkarma veya çarpma/bölme gibi birbirinin tersi olan iki eylemdir. Bu nedenle, türev bulma konusunda bir beceri ve bir tür deneyim olmadan, ne yazık ki, daha fazla ilerleyemez.

Bu bağlamda, aşağıdaki metodolojik materyallere ihtiyacımız olacak: türev tablosu ve integral tablosu.

Belirsiz integralleri çalışmanın zorluğu nedir? Türevlerde kesinlikle 5 farklılaşma kuralı, bir türev tablosu ve oldukça açık bir eylem algoritması varsa, o zaman integrallerde her şey farklıdır. Onlarca entegrasyon yöntemi ve tekniği var. Ve, entegrasyon yöntemi başlangıçta yanlış seçilmişse (yani, nasıl çözüleceğini bilmiyorsanız), o zaman integral, çeşitli hileleri ve püf noktalarını fark etmeye çalışan gerçek bir bilmece gibi, kelimenin tam anlamıyla günlerce “deliklenebilir”. . Hatta bazıları bundan hoşlanıyor.

Bu arada, öğrencilerden (beşeri bilimlerden değil) sık sık şöyle bir görüş duyduk: “Limit veya türevi çözmekle hiç ilgilenmedim, ancak integraller tamamen farklı bir konudur, heyecan verici, her zaman “ crack "karmaşık bir integral" . Durmak. Yeter kara mizah, hadi bu çok belirsiz integrallere geçelim.

Çözmenin birçok yolu olduğuna göre, bir çaydanlık belirsiz integralleri incelemeye nereden başlar? İntegral hesapta, bize göre, her şeyin etrafında döndüğü üç sütun veya bir tür "eksen" vardır. Her şeyden önce, en basit integralleri iyi anlamalısınız (bu makale).

O zaman dersi ayrıntılı olarak çalışmanız gerekir. BU EN ÖNEMLİ RESEPSİYON! İntegrallere ayrılmış tüm makalelerin belki de en önemli makalesi. Üçüncüsü, mutlaka okuyun Parçalara göre entegrasyon, çünkü geniş bir işlev sınıfını bütünleştirir. En azından bu üç derste ustalaşırsanız, zaten “iki değil” vardır. Bilmediğin için affedebilirsin trigonometrik fonksiyonların integralleri, kesirlerin integralleri, kesirli rasyonel fonksiyonların integralleri, irrasyonel fonksiyonların integralleri (kökler), ancak değiştirme yönteminde veya parça yöntemiyle entegrasyonda “bir su birikintisine girerseniz”, çok, çok kötü olacaktır.

Öyleyse, basit başlayalım. İntegral tablosuna bakalım. Türevlerde olduğu gibi, birkaç integrasyon kuralı ve bazı temel fonksiyonların bir integral tablosunu görüyoruz. Herhangi bir tablo integrali (ve aslında herhangi bir belirsiz integral) şu şekildedir:

Doğrudan gösterime ve terimlere geçelim:

- ayrılmaz simgesi.

- integrand işlevi ("s" harfiyle yazılmıştır).

– diferansiyel simgesi. Ne olduğunu, çok yakında ele alacağız. Ana şey, integrali yazarken ve çözüm sırasında bu simgeyi kaybetmemek önemlidir. Gözle görülür bir kusur olacaktır.

integralin integrali veya "doldurulmasıdır".

– ters türev işlev.

– . Terimlerle çok yüklenmeye gerek yok, buradaki en önemli şey, herhangi bir belirsiz integralde cevaba bir sabit eklenmesidir.

Belirsiz bir integrali çözmek içinters türev fonksiyonlar seti verilen integralden

Girişe tekrar bir göz atalım:

İntegral tablosuna bakalım.

Ne oluyor? sol taraflarımız dönüyorlar diğer işlevler için: .

Tanımımızı basitleştirelim:

Belirsiz integrali çözün - onu belirsiz (sabite kadar) bir fonksiyona DÖNÜŞTÜRMEK anlamına gelir , bazı kurallar, teknikler ve bir tablo kullanarak.

Örneğin, tablo integralini alın . Ne oldu? Sembolik kayıt, bir dizi ters türev fonksiyonuna dönüşmüştür.

Türevlerde olduğu gibi, integrallerin nasıl bulunacağını öğrenmek için teorik açıdan integralin veya ters türev fonksiyonun ne olduğunun farkında olmak gerekli değildir. Sadece bazı biçimsel kurallara göre dönüşümler yapmak yeterlidir. Yani, durumda integralin neden tam olarak dönüştüğünü anlamak hiç de gerekli değildir. Bunu ve diğer formülleri hafife alabilirsiniz. Herkes elektrik kullanır, ancak çok az insan elektronların teller boyunca nasıl hareket ettiğini düşünür.

Türev alma ve entegrasyon zıt işlemler olduğundan, doğru bulunan herhangi bir ters türev için aşağıdakiler doğrudur:

Başka bir deyişle, doğru cevap türevlenirse, orijinal integralin elde edilmesi gerekir.

Aynı tablo integraline geri dönelim .

Bu formülün geçerliliğini doğrulayalım. Sağ tarafın türevini alıyoruz:

orijinal integraldir.

Bu arada, bir fonksiyona neden her zaman bir sabitin atandığı daha açık hale geldi. Türev alırken, bir sabit her zaman sıfıra dönüşür.

Belirsiz integrali çözün bulmak demektir bir demet Tümü antitürevler ve tek bir işlev değil. İncelenen tablo örneğinde, , , , vb. - tüm bu fonksiyonlar integralin çözümüdür. Sonsuz sayıda çözüm var, bu yüzden kısaca şöyle yazıyorlar:

Bu nedenle, herhangi bir belirsiz integralin kontrol edilmesi yeterince kolaydır. Bu, farklı türlerdeki çok sayıda integral için bir miktar telafidir.

Spesifik örneklere geçelim. Türev çalışmasında olduğu gibi, iki entegrasyon kuralıyla başlayalım:

- devamlı C integral işaretinden çıkarılabilir (ve alınmalıdır).

– iki fonksiyonun toplamının (farkının) integrali, iki integralin toplamına (farkının) eşittir. Bu kural herhangi bir sayıda terim için geçerlidir.

Gördüğünüz gibi, kurallar temelde türevlerle aynıdır. Bazen denir doğrusallık özellikleri integral.

örnek 1

Belirsiz integrali bulun.

Bir kontrol yapın.

Karar: Gibi dönüştürmek daha uygundur.

(1) Kuralın uygulanması . Diferansiyel simgesini yazmayı unutmayın dx her integralin altında. Neden her birinin altında? dxtam çarpanıdır. Ayrıntılı olarak boyarsanız, ilk adım aşağıdaki gibi yazılmalıdır:

(2) Kurala göre tüm sabitleri integrallerin işaretlerinden alıyoruz. Dikkat edin, son dönemde tg 5 bir sabittir, onu da çıkarırız.

Ayrıca bu adımda entegrasyon için kökleri ve dereceleri hazırlıyoruz. Farklılaşmada olduğu gibi, kökler formda temsil edilmelidir. . Paydada bulunan kökler ve dereceler - yukarı hareket ettirin.

Not: türevlerden farklı olarak, integrallerdeki köklerin her zaman forma indirgenmesi gerekmez ve dereceleri yukarı hareket ettirin.

Örneğin, - bu, sizden önce zaten hesaplanmış olan hazır bir tablo integralidir ve her türlü Çin hilesi gibi tamamen gereksiz. Benzer şekilde: - bu aynı zamanda bir tablo integralidir, formda bir kesri temsil etmenin bir anlamı yoktur . Tabloyu dikkatlice inceleyin!

(3) Tüm integraller tablo şeklindedir. Formülleri kullanarak tabloyu kullanarak dönüşümü gerçekleştiriyoruz: , ve

bir güç işlevi için - .

Tablo integralinin, bir güç fonksiyonu için formülün özel bir hali olduğuna dikkat edilmelidir: .

Devamlı C sadece ifadenin sonuna bir kez ekleyin

(onları her integralin arkasına koymak yerine).

(4) Elde edilen sonucu, formun tüm dereceleri olduğunda daha kompakt bir biçimde yazarız.

yine kökler olarak temsil edilir ve negatif üslü güçler paydaya geri sıfırlanır.

muayene Kontrolü gerçekleştirmek için alınan cevabı ayırt etmeniz gerekir:

İlk integrand, yani, integral doğru bulundu. Dans ettiklerinden buna döndüler. İntegrali olan hikayenin böyle bitmesi güzel.

Zaman zaman belirsiz integrali kontrol etmek için biraz farklı bir yaklaşım vardır, türev değil, ancak cevaptan diferansiyel alınır:

Sonuç olarak, bir integrant değil, bir integrant elde ederiz.

Diferansiyel kavramından korkmayın.

Diferansiyel, türev ile çarpımıdır dx.

Ancak, bizim için önemli olan teorik incelikler değil, bu farkla sonra ne yapılacağıdır. Diferansiyel şu şekilde ortaya çıkar: simge d kaldırın, parantezin sağına bir çizgi koyun, ifadenin sonuna bir çarpan atayın dx :

alınan orijinal integrand, yani integral doğru bulunur.

Gördüğünüz gibi, diferansiyel türevi bulmaya geliyor. Daha az kontrol etmenin ikinci yolunu seviyorum, çünkü ek olarak büyük parantezler çizmem ve diferansiyel simgesini sürüklemem gerekiyor. dx testin sonuna kadar. Daha doğru veya "daha sağlam" veya başka bir şey olmasına rağmen.

Aslında, ikinci doğrulama yöntemi hakkında sessiz kalmak mümkündü. Mesele yöntemde değil, diferansiyeli açmayı öğrenmiş olmamızdır. Tekrar.

Diferansiyel aşağıdaki gibi ortaya çıkar:

1) simge d kaldırmak;

2) parantezin üzerine sağ tarafa bir vuruş koyun (türevin tanımı);

3) ifadenin sonunda bir faktör atarız dx .

Örneğin:

Hatırla bunu. Çok yakında düşünülen tekniğe ihtiyacımız olacak.

Örnek 2

Belirsiz bir integral bulduğumuzda, DAİMA kontrol etmeye çalışırız.Üstelik bunun için büyük bir fırsat var. Yüksek matematikteki tüm problem türleri bu bakış açısından bir hediye değildir. Kontrol görevlerinde genellikle doğrulamanın gerekli olmadığı önemli değildir, hiç kimse ve hiçbir şey taslak üzerinde yapılmasını engellemez. Bir istisna ancak yeterli zaman olmadığında yapılabilir (örneğin, testte, sınavda). Şahsen, her zaman integralleri kontrol ederim ve doğrulama eksikliğini bir hack ve eksik tamamlanmış bir görev olarak görüyorum.

Örnek 3

Belirsiz integrali bulun:

. Bir kontrol yapın.

Çözüm: İntegrali analiz ettiğimizde, integralin altında iki fonksiyonun çarpımına ve hatta tüm ifadenin üslü olmasına sahip olduğumuzu görüyoruz. Ne yazık ki, bütünleşik savaş alanında Numara iyi ve rahat çarpım ve bölümü entegre etmek için formüller gibi: veya .

Bu nedenle, bir çarpım veya bölüm verildiğinde, integrali toplamanın mümkün olup olmadığını görmek her zaman mantıklıdır? Dikkate alınan örnek, mümkün olduğu durumdur.

İlk önce tam çözümü veriyoruz, yorumlar aşağıda olacak.

(1) Herhangi bir gerçek sayının toplamının karesi için eski güzel formülü kullanırız, ortak parantezin üzerindeki dereceden kurtuluruz. parantezlerin dışında ve kısaltılmış çarpma formülünü ters yönde uygulayarak: .

Örnek 4

belirsiz integrali bulun

Bir kontrol yapın.

Bu kendi kendine çözme için bir örnektir. Dersin sonunda cevaplayın ve çözümü tamamlayın.

Örnek 5

belirsiz integrali bulun

. Bir kontrol yapın.

Bu örnekte, integral bir kesirdir. İntegranda bir kesir gördüğümüzde ilk akla gelen soru şu olmalıdır: “Bu kesirden bir şekilde kurtulmak ya da en azından basitleştirmek mümkün müdür?”.

Paydanın yalnız bir "x" kökü içerdiğini fark ettik. Alandaki kişi bir savaşçı değil, yani payı payda terime göre terime bölebilirsiniz:

Bir fonksiyonun türeviyle ilgili makalelerde defalarca tartışıldığı için kesirli kuvvetlere sahip eylemler hakkında yorum yapmıyoruz.

Hala böyle bir örnekle kafanız karıştıysa

ve kimse doğru cevabı alamaz,

Ayrıca çözümün bir adımı atladığını, yani kuralların uygulandığını unutmayın. , . Genellikle, integral çözme konusunda belirli bir deneyime sahip olan bu kurallar, açık bir gerçek olarak kabul edilir ve ayrıntılı olarak açıklanmaz.

Örnek 6

Belirsiz integrali bulun. Bir kontrol yapın.

Bu kendi kendine çözme için bir örnektir. Dersin sonunda cevaplayın ve çözümü tamamlayın.

Genel durumda, integrallerdeki kesirler ile her şey o kadar basit değildir, makalede bazı türlerdeki kesirlerin entegrasyonu hakkında ek materyaller bulunabilir: Bazı kesirlerin integrali. Ancak, yukarıdaki makaleye geçmeden önce dersi okumanız gerekir: Belirsiz integralde yer değiştirme yöntemi. Gerçek şu ki, bir fonksiyonu diferansiyel veya değişken değiştirme yöntemi altında toplamak, kilit nokta Konunun incelenmesinde, yalnızca "değiştirme yöntemi için saf atamalarda" değil, aynı zamanda diğer birçok integral türünde de ortaya çıktığı için.

Çözümler ve cevaplar:

Örnek 2: Çözüm:

Örnek 4: Çözüm:

Bu örnekte, indirgenmiş çarpma formülünü kullandık.

Örnek 6: Çözüm:

Belirsiz bir integralde bir değişkeni değiştirme yöntemi. Çözüm örnekleri

Bu derste, belirsiz integralleri çözme sürecinde kullanılan en önemli ve en yaygın hilelerden biri olan değişken yönteminin değiştirilmesi ile tanışacağız. Materyalde başarılı bir şekilde ustalaşmak için başlangıç bilgisi ve entegrasyon becerileri gereklidir. İntegral hesabında boş bir dolu çaydanlık hissi varsa, önce malzemeye aşina olmalısınız. Belirsiz integral. Çözüm örnekleri, burada integralin ne olduğu erişilebilir bir biçimde açıklanır ve yeni başlayanlar için temel örnekler ayrıntılı olarak analiz edilir.

Teknik olarak, belirsiz bir integralde bir değişkeni değiştirme yöntemi iki şekilde uygulanır:

– Fonksiyonu diferansiyelin işareti altına getirmek.

– Değişkenin gerçek değişimi.

Aslında aynı şey ama çözümün tasarımı farklı görünüyor. Daha basit bir durumla başlayalım.