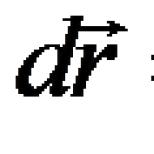Sınırlı fonksiyon tanımı nedir? Monoton fonksiyonların limitleri. Konuyla ilgili ders ve sunum: "Bir fonksiyonun özellikleri. Fonksiyonun artması ve azalması"

Tüm tanımların, işlevin etki alanının bir parçası olan sayısal bir X kümesi içerdiğine dikkat edin: X ve D(f). Uygulamada, çoğu zaman X'in sayısal bir aralık olduğu durumlar vardır (bölüm, aralık, ışın vb.).

Tanım 1.

Bir y \u003d f (x) işlevine, X kümesinin herhangi iki noktası için x 1 ve x 2 olacak şekilde, D (f) ile bir X kümesinde artan denir.< х 2 , выполняется неравенство f(х 1 < f(х 2).

Tanım 2.

Bir y \u003d f (x) işlevine, X kümesinin iki noktasının x 1 ve x 2'sinin herhangi bir monotonluğu için, x 1 olacak şekilde, D (f) ile bir X kümesinde azalan denir.< х 2 , функции выполняется неравенство f(x 1) >f(x2).

Pratikte, aşağıdaki formülleri kullanmak daha uygundur: argümanın daha büyük değeri, fonksiyonun daha büyük değerine tekabül ederse, fonksiyon artar; bağımsız değişkenin daha büyük değeri, işlevin daha küçük değerine karşılık geliyorsa, işlev azalır.

7. ve 8. sınıflarda, artan veya azalan fonksiyonlar kavramlarının aşağıdaki geometrik yorumunu kullandık: artan bir fonksiyonun grafiği boyunca soldan sağa hareket ederek, bir nevi tepeye tırmanırız (Şekil 55); bir yokuştan aşağı iniyormuşuz gibi, azalan bir fonksiyonun grafiği boyunca soldan sağa doğru hareket ediyoruz (Şekil 56).
Genellikle "artan fonksiyon", "azalan fonksiyon" terimleri monotonik fonksiyon ortak adıyla birleştirilir ve artan veya azalan bir fonksiyonun çalışmasına monotonluk fonksiyonunun çalışması denir.

Bir duruma daha dikkat çekiyoruz: eğer bir fonksiyon doğal alanında artıyorsa (veya azalıyorsa), o zaman genellikle fonksiyonun arttığı (veya azaldığı) söylenir - sayı kümesini belirtmeden X.

örnek 1

Monotonluk için işlevi inceleyin:

a) y \u003d x 3 + 2; b) y \u003d 5 - 2x.

Karar:

a) x 1 ve x 2 argümanının keyfi değerlerini alın ve x 1'e izin verin<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

Son eşitsizlik, f(x 1) anlamına gelir< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).

Yani x 1'den< х 2 следует f(х 1) >f(x 2), yani verilen fonksiyon azalıyor (sayı doğrusunda).

Tanım 3.

X kümesindeki fonksiyonun tüm değerleri belirli bir sayıdan büyükse (yani bir herhangi bir x є X değeri için f( x) >m) eşitsizliği olacak şekilde m sayısı.

Tanım 4.

y \u003d f (x) işlevi, işlevin tüm değerleri belirli bir sayıdan küçükse (başka bir deyişle, öyle bir M sayısı varsa) D (f) ile X kümesinde yukarıdan sınırlandırılmış olarak adlandırılır. herhangi bir x є X değeri için f (x) eşitsizliği< М).

X kümesi belirtilmemişse, fonksiyonun tüm tanım alanında aşağıdan veya yukarıdan sınırlandığı varsayılır.

Bir fonksiyon hem aşağıdan hem de yukarıdan sınırlandırılmışsa, buna sınırlı denir.

Bir fonksiyonun sınırlılığı grafiğinden kolayca okunur: eğer fonksiyon aşağıdan sınırlandırılmışsa, grafiği tamamen bazı yatay y \u003d m çizgisinin üzerinde bulunur (Şek. 57); fonksiyon yukarıdan sınırlandırılmışsa, grafiği tamamen bazı yatay y \u003d M çizgisinin altında bulunur (Şek. 58).

Örnek 2 Sınırlılık için bir işlevi araştırmak
Karar. Bir yandan, eşitsizlik oldukça açıktır (kare kökün tanımına göre, bu, fonksiyonun aşağıdan sınırlandırıldığı anlamına gelir. Öte yandan, elimizde ve dolayısıyla
Bu, fonksiyonun yukarıdan sınırlandığı anlamına gelir. Şimdi verilen fonksiyonun grafiğine bakın (önceki paragraftan Şekil 52). Fonksiyonun hem yukarıdan hem de aşağıdan sınırlılığı grafikten oldukça kolay okunur.

Tanım 5.

M sayısına, aşağıdaki durumlarda X C D (f) kümesindeki y \u003d f (x) işlevinin en küçük değeri denir:

1) X'de öyle bir x 0 noktası vardır ki f(x 0) = m;

2) X'ten tüm x'ler için m>f(х 0) eşitsizliği sağlanır.

Tanım 6.

M sayısına, X C D (f) kümesindeki y \u003d f (x) işlevinin en büyük değeri denir, eğer:
1) X'de öyle bir x 0 noktası vardır ki f(x 0) = M;
2) X'ten tüm x'ler için eşitsizlik
7. ve 8. sınıflarda fonksiyonun en küçük değerini y sembolü ile, en büyük değerini y sembolü ile gösterdik.

X kümesi belirtilmemişse, tüm tanım alanında fonksiyonun en küçük veya en büyük değerini bulmaktan bahsettiğimiz varsayılır.

Aşağıdaki faydalı ifadeler oldukça açıktır:

1) Bir fonksiyon Y'ye sahipse, aşağıdan sınırlandırılır.
2) Bir fonksiyon Y'ye sahipse, yukarıdan sınırlandırılır.
3) Fonksiyon aşağıda sınırlı değilse, Y yoktur.
4) Fonksiyon yukarıdan sınırlı değilse, Y yoktur.

Örnek 3

Bir fonksiyonun en küçük ve en büyük değerlerini bulun
Karar.

Özellikle fonksiyon grafiğine başvurursanız (Şekil 52), bu \u003d 0 (fonksiyon bu değere x \u003d -3 ve x \u003d 3 noktalarında ulaşır), a \u003d 3 (şekil 52) oldukça açıktır. fonksiyon bu değere x \u003d 0 noktasında ulaşır.
7. ve 8. sınıfta fonksiyonların iki özelliğine daha değinmiştik. Birincisi, bir fonksiyonun dışbükeylik özelliği olarak adlandırıldı. Grafiğin herhangi iki noktasını (X'ten apsislerle) düz bir çizgi parçasıyla birleştirerek, grafiğin ilgili bölümünün çizilen parçanın altında olduğunu bulursak, bir fonksiyonun X aralığında aşağı doğru dışbükey olduğu kabul edilir ( 59). süreklilik Bir fonksiyon, grafiğinin herhangi iki noktasını (X'ten apsislerle) düz bir çizgi parçası ile birleştirerek, grafiğin ilgili bölümünün çizilen parçanın üzerinde olduğunu bulursak, X aralığında yukarı doğru dışbükeydir (Şekil 60). ).

İkinci özellik - fonksiyonun X aralığında sürekliliği - X aralığında fonksiyonun grafiğinin sürekli olduğu anlamına gelir, yani. delinme ve sıçrama yoktur.

Yorum.

Aslında, matematikte, dedikleri gibi, her şey “tam tersidir”: bir fonksiyonun grafiği, yalnızca fonksiyonun sürekliliği kanıtlandığında düz bir çizgi (delinmeler ve sıçramalar olmadan) olarak gösterilir. Ancak bir fonksiyonun sürekliliğinin oldukça karmaşık ve ince olan biçimsel tanımı henüz bizim gücümüzün ötesindedir. Aynısı bir fonksiyonun dışbükeyliği için de söylenebilir. Fonksiyonların bu iki özelliğini tartışırken, görsel-sezgisel temsillere güvenmeye devam edeceğiz.

Şimdi bilgimizi gözden geçirelim. 7. ve 8. sınıflarda incelediğimiz fonksiyonları hatırlayarak, grafiklerinin nasıl göründüğünü açıklayacağız ve fonksiyonun özelliklerini belirli bir sıraya bağlı kalarak listeleyeceğiz, örneğin: tanım alanı; monoton; sınırlama; , ; süreklilik; değer aralığı; dışbükey.

Ardından, fonksiyonların yeni özellikleri görünecek ve özellikler listesi buna göre değişecektir.

1. Sabit fonksiyon y \u003d C

Y \u003d C fonksiyonunun grafiği, Şek. 61 - x eksenine paralel düz çizgi. Bu o kadar ilginç olmayan bir işlevdir ki, özelliklerini listelemenin bir anlamı yoktur.

y \u003d kx + m fonksiyonunun grafiği düz bir çizgidir (Şek. 62, 63).

y \u003d kx + m fonksiyonunun özellikleri:

1)
2) k > 0 ise artar (Şekil 62), k ise azalır< 0 (рис. 63);

4) ne en büyük ne de en küçük değerler vardır;
5) fonksiyon süreklidir;
6)
7) dışbükeylik hakkında konuşmak mantıklı değil.

y \u003d kx 2 fonksiyonunun grafiği, orijinde bir tepe noktası olan ve k\u003e O (Şekil 64) ise dalları yukarı doğru ve k ise aşağı doğru yönlendirilmiş bir paraboldür.< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

y - kx 2 fonksiyonunun özellikleri:

k > 0 durumu için (Şekil 64):

1) D(f) = (-oo,+oo);


4) = mevcut değil;
5) sürekli;
6) Е(f) = fonksiyon azalır ve aralıkta , ışın üzerinde azalır;
7) yukarı doğru dışbükey.

y \u003d f (x) fonksiyonunun grafiği nokta nokta oluşturulur; (x; f (x)) formundan ne kadar çok puan alırsak, grafiğin fikri o kadar doğru olur. Bu noktaların çoğunu alırsak, grafik fikri daha eksiksiz olacaktır. Bu durumda sezgi bize grafiğin düz bir çizgi olarak (bu durumda bir parabol olarak) çizilmesi gerektiğini söyler. Ve sonra grafiği okuyarak, fonksiyonun sürekliliği, aşağı veya yukarı dışbükeyliği, fonksiyonun aralığı hakkında sonuçlar çıkarıyoruz. Listelenen yedi özellikten sadece 1), 2), 3), 4)'ün, kesin tanımlara atıfta bulunarak bunları kanıtlayabildiğimiz anlamda "yasal" olduğunu anlamalısınız. Kalan özellikler hakkında sadece görsel-sezgisel temsillerimiz var. Bu arada, bunda yanlış bir şey yok. Matematiğin gelişim tarihinden, insanlığın kesin tanımları bilmeden, belirli nesnelerin çeşitli özelliklerini sıklıkla ve uzun süre kullandığı bilinmektedir. Sonra, bu tür tanımlar formüle edilebildiğinde, her şey yerine oturdu.

Fonksiyonun grafiği bir hiperboldür, koordinat eksenleri hiperbolün asimptotları olarak işlev görür (Şekil 66, 67).

1) D(f) = (-00.0)1U (0.+oo);
2) k > 0 ise, fonksiyon açık ışında (-oo, 0) ve açık ışında (0, +oo) azalır (Şekil 66); Eğer< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) ne aşağıdan ne de yukarıdan sınırlı değildir;
4) ne en küçük ne de en büyük değerler vardır;
5) fonksiyon açık ışında (-oo, 0) ve açık ışında (0, +oo) süreklidir;
6) E(f) = (-oo, 0) U (0, + oo);
7) k > 0 ise, fonksiyon x'te yukarı doğru dışbükeydir< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, yani açık kirişte (0, +oo) (Şek. 66). Eğer< 0, то функция выпукла вверх при х >o ve x'de aşağı dışbükey< О (рис. 67).
Fonksiyonun grafiği parabolün bir dalıdır (Şekil 68). Fonksiyon Özellikleri :
1) D(f) = , ışında artar. Bu segmentte $16-x^2≤16$ veya $\sqrt(16-x^2)≤4$, ancak bu yukarıdan sınırlılık anlamına gelir.
Cevap: fonksiyonumuz $y=0$ ve $y=4$ olmak üzere iki satırla sınırlıdır.

En yüksek ve en düşük değer

Х⊂D(f) kümesindeki y= f(x) fonksiyonunun en küçük değeri bir m sayısıdır, öyle ki:

b) Herhangi bir xϵX için $f(x)≥f(x0)$ tutar.

Х⊂D(f) kümesindeki y=f(x) fonksiyonunun en büyük değeri bir m sayısıdır, öyle ki:
a) $f(x0)=m$ olacak şekilde bazı x0 vardır.
b) Herhangi bir xϵX için $f(x)≤f(x0)$ sağlanır.

En büyük ve en küçük değer genellikle y max ile gösterilir. ve y adı. .

Sınırlılık ve bir fonksiyonun en küçük değerine sahip en büyüğü kavramları yakından ilişkilidir. Aşağıdaki ifadeler doğrudur:
a) Bir fonksiyon için en küçük değer varsa, alttan sınırlanır.
b) Bir fonksiyon için bir maksimum değer varsa, o zaman yukarıdan sınırlandırılır.
c) Fonksiyon yukarıdan sınırlandırılmamışsa maksimum değer yoktur.
d) Fonksiyon aşağıda sınırlı değilse, en küçük değer yoktur.

$y=\sqrt(9-4x^2+16x)$ fonksiyonunun en büyük ve en küçük değerini bulun.
Çözüm: $f(x)=y=\sqrt(9-4x^2+16x)=\sqrt(9-(x-4)^2+16)=\sqrt(25-(x-4)^2 )≤5$.
$x=4$ $f(4)=5$ için diğer tüm değerler için fonksiyon daha küçük değerler alır veya yoktur, yani bu fonksiyonun en büyük değeridir.
Tanım olarak: $9-4x^2+16x≥0$. $(2x+1)(2x-9)≥0$ kare trinomunun köklerini bulun. $x=-0.5$ ve $x=4.5$'da fonksiyon kaybolur, diğer tüm noktalarda sıfırdan büyüktür. O halde, tanım gereği, fonksiyonun en küçük değeri sıfırdır.
Cevap: y maks. =5 ve y dak. =0.

Beyler, bir fonksiyonun dışbükeylik kavramlarını da inceledik. Bazı problemleri çözerken bu özelliğe ihtiyacımız olabilir. Bu özellik ayrıca grafikler kullanılarak kolayca belirlenir.

Orijinal fonksiyonun grafiğinin herhangi iki noktası bağlıysa ve fonksiyonun grafiği noktaları birleştiren çizginin altındaysa, fonksiyon aşağı doğru dışbükeydir.

Orijinal fonksiyonun grafiğinin herhangi iki noktası birbirine bağlıysa ve fonksiyonun grafiği noktaları birleştiren çizginin üzerindeyse, fonksiyon yukarı doğru dışbükeydir.

Yukarıdaki fonksiyonun grafiği gibi, fonksiyonumuzun grafiğinde süreksizlik yoksa bir fonksiyon süreklidir.

Bir fonksiyonun özelliklerini bulmak istiyorsanız, özellikleri arama sırası aşağıdaki gibidir:
a) Tanım alanı.
b) Monotonluk.
c) sınırlama.
d) En büyük ve en küçük değer.
e) Süreklilik.
f) Değer aralığı.

$y=-2x+5$ fonksiyonunun özelliklerini bulun.
Karar.
a) Tanım alanı D(y)=(-∞;+∞).
b) Monotonluk. Herhangi bir x1 ve x2 değerini kontrol edelim ve x1'e izin verelim< x2.
$f(x1)=-2x1+2$.
$f(x2)=-2x2+2$.
çünkü x1< x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
c) sınırlama. Açıkçası, işlev sınırlı değildir.
d) En büyük ve en küçük değer. Fonksiyon sınırlı olmadığı için maksimum veya minimum değer yoktur.
e) Süreklilik. Fonksiyonumuzun grafiğinde boşluk yok, o zaman fonksiyon sürekli.
f) Değer aralığı. E(y)=(-∞;+∞).

Bağımsız çözüm için bir fonksiyonun özelliklerine ilişkin görevler

Eğer böyle bir sayı varsa, A kümesindeki y=f(x) BOUNDED UP (BOTTOM) fonksiyonunu D(f) alanından çağıracağız. M , bu koşuldan herhangi bir x için

Mantıksal semboller kullanılarak tanım şu şekilde yazılabilir:

f(x) – sette yukarıdan sınırlı

(f(x) – sette aşağıdan sınırlı

Mutlak değerle sınırlandırılmış veya basitçe sınırlandırılmış fonksiyonlar da dikkate alınır.

Eğer pozitif bir M sayısı varsa, A kümesinde BOUNDED fonksiyonunu tanım alanından çağıracağız.

Mantıksal sembollerin dilinde

f(x) – sette sınırlı

Sınırlı olmayan bir fonksiyona sınırsız denir. Olumsuzlama yoluyla verilen tanımların çok az içeriğe sahip olduğunu biliyoruz. Bu iddiayı bir tanım olarak formüle etmek için niceleyici işlemlerin (3.6) ve (3.7) özelliklerini kullanırız. O zaman mantıksal sembollerin dilinde fonksiyonun sınırlılığının inkarı şunları verecektir:

f(x) – sette sınırlı

Elde edilen sonuç, aşağıdaki tanımı formüle etmemizi sağlar.

Herhangi bir pozitif M sayısı için bu kümede x argümanının böyle bir değeri varsa, fonksiyonun etki alanına ait olan A kümesinde bir fonksiyona SINIRSIZ denir. , değerin yine de M'nin değerini aşacağını, yani .

Örnek olarak, işlevi düşünün

Tüm reel eksen üzerinde tanımlanır. [–2;1] parçasını (A kümesi) alırsak, üzerinde hem yukarıdan hem de aşağıdan sınırlandırılacaktır.

Gerçekten de, yukarıdan sınırlı olduğunu göstermek için, yüklemi dikkate almalıyız.

ve [–2;1] segmentinde alınan tüm x için doğru olacak şekilde M olduğunu (var olduğunu) gösterin.

Böyle bir M bulmak zor değil. M = 7 olduğunu varsayabiliriz, varlık niceleyicisi en az bir M değeri bulmayı ima eder. Böyle bir M'nin varlığı, [–2;1] segmentindeki fonksiyonun yukarıdan sınırlı olduğu gerçeğini doğrular.

Aşağıdan sınırlılığını kanıtlamak için, yüklemi dikkate almalıyız.

Bu yüklemin doğruluğunu sağlayan M değeri örneğin M = -100'dür.

Fonksiyonun modulo ile sınırlı olacağı da kanıtlanabilir: [–2;1] segmentindeki tüm x için, fonksiyonun değerleri değerleri ile çakışır, bu nedenle M olarak alabiliriz , örneğin, M = 7'nin önceki değeri.

Aynı fonksiyonun aralıkta sınırsız olacağını gösterelim, yani,

Böyle bir x'in var olduğunu göstermek için şu ifadeyi göz önünde bulundurun:

Argümanın pozitif değerleri arasında x'in gerekli değerlerini arayarak elde ederiz.

Bu demektir ki Mwe ne kadar pozitif alırsa alsın eşitsizliğin sağlanmasını sağlayan x değerleri

oranından elde edilir.

Tüm reel eksen üzerinde bir fonksiyon göz önüne alındığında, mutlak değerde sınırsız olduğu gösterilebilir.

Gerçekten de eşitsizlikten

Yani pozitif M ne kadar büyük olursa olsun ya da eşitsizliğin gerçekleşmesini sağlayacaktır.

AŞIRI FONKSİYON.

Fonksiyon noktada vardır ile yerel maksimum (minimum) bu noktanın böyle bir komşuluğu varsa, x¹ ile bu mahalle eşitsizliği tatmin ediyor

özellikle uç nokta aralığın sadece bir iç noktası olabilir ve f(x) burada tanımlanmalıdır. Bir ekstremumun bulunmadığı olası durumlar, Şek. 8.8.

Bir fonksiyon belirli bir aralıkta artıyorsa (azalıyorsa) ve belirli bir aralıkta azalıyorsa (artıyorsa), o zaman nokta ile yerel maksimum (minimum) noktadır.

Bir noktada f(x) fonksiyonunun bir maksimumunun olmaması ile şu şekilde formüle edilebilir:

_______________________

f(x) c'de bir maksimuma sahiptir

Bu, eğer c noktası yerel bir maksimum nokta değilse, o zaman c noktasını bir iç nokta olarak içeren komşuluk ne olursa olsun, c'ye eşit olmayan en az bir x değeri vardır, bunun için . Bu nedenle, c noktasında maksimum yoksa, bu noktada hiç ekstremum olmayabilir veya minimum nokta olabilir (Şekil 8.9).

Ekstremum kavramı, bir fonksiyonun herhangi bir noktadaki değerinin yakındakilere göre karşılaştırmalı bir değerlendirmesini verir. Bir aralığın tüm noktaları için benzer bir fonksiyon değerleri karşılaştırması yapılabilir.

Bir kümedeki bir fonksiyonun EN BÜYÜK (MİNİMUM) değeri, bu kümeden bir noktadaki değeridir, öyle ki – için. Fonksiyonun en büyük değerine segmentin iç noktasında ulaşılır ve en küçük değere – sol ucunda.

Bir segmentte verilen bir fonksiyonun en büyük (en küçük) değerini belirlemek için, maksimumlarının (minimumlarının) tüm değerleri arasından en büyük (en küçük) sayının yanı sıra alınan değerlerin seçilmesi gerekir. aralığın sonları. Fonksiyonun en büyük (en küçük) değeri olacaktır. Bu kural daha sonra belirtilecektir.

Açık bir aralıkta bir fonksiyonun en büyük ve en küçük değerlerini bulma sorunu her zaman kolay çözülmez. Örneğin, işlev

aralıkta (Şekil 8.11) bunlara sahip değil.

Örneğin, bu fonksiyonun en büyük değere sahip olmadığından emin olalım. Nitekim, fonksiyonun monotonluğu göz önüne alındığında, x'in değerlerini birliğin soluna ne kadar yakın ayarlasak da, fonksiyonun değerlerinin daha büyük olacağı başka x'lerin olacağı iddia edilebilir. değerleri verilen sabit noktalarda, ancak yine de birlikten daha az.