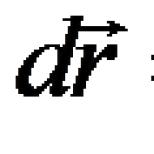Bir fonksiyonun 2. mertebesinin kısmi türevlerini bulun. Misal. y x fonksiyonunun kısmi türevlerini bulun. Bir fonksiyonun kısmi türevleri ve toplam diferansiyeli

Misal. y x yxz fonksiyonunun kısmi türevlerini bulun

Karar. y = const ayarlandığında, xy x z'yi buluruz

x =const ayarını yaparsak 2 2) 1 (1 y x x y xx y z buluruz)

Misal. M (1, - 1, 0) noktasında fonksiyonun kısmi türevlerinin değerlerini bulun. xyzyxu)ln(

Karar. y = sabit , z = sabit , 10 11 22 1)02(1 22 22 , Ì czy yz yx x yzx yxx u'yu buluruz)

Benzer şekilde, 10 11 22 1)20(1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z u buluyoruz)

Kısmi türevin geometrik anlamı (örneğin), M 0 (x 0, y 0, z 0) noktasında çizilen teğetin eğiminin y \u003d y 0 düzlemiyle yüzey bölümüne tanjantıdır. xz

z = f (x , y) fonksiyonunun sürekli kısmi türevleri olduğunu varsayalım), (yxf x z x), (yxf y z y

Bu türevler, bağımsız değişkenler x ve y'nin fonksiyonlarıdır. 1. mertebeden kısmi türevler de diyeceğiz.), (yxf x), (yxf y

2. mertebeden kısmi türevlere 1. mertebeden kısmi türevlerin kısmi türevleri denir. İki değişkenli bir z \u003d f (x, y) işlevi için, aşağıdaki mod ile gösterilen 2. mertebeden dört kısmi türev bulunabilir:

Genel durumda, karışık kısmi türevler çakışmayabilir, ancak aşağıdaki teorem onlar için doğrudur: Teorem. Karışık kısmi türevler ve bir M (x, y) noktasında sürekli ise, bunlar eşittir, yani xyfyxf), (yxfyxf yxxy

n'inci dereceden kısmi türevler, (n-1)-inci dereceden kısmi türevlerin kısmi türevleridir. Belirtilirler, vb. 221 , yx z x z n n n

Misal. Fonksiyonun 2. mertebesinin kısmi türevlerini bulun)1 sin(23 xyyxz

Karar. art arda bulun); 1 cos(3 22 xyyyx x zcy); 1 cos(2 3 xyxyx y z cx

); 1 sin(6)1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy); 1 günah()1 cos(6)1 cos(3 2 22 2 xyyx xyyyx z cx cx

)1 günah()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy)1 günah(2)1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx

z = f(x, y) fonksiyonunu düşünün. x argümanına bir artış Δ x ve y argümanına bir artış Δ y verelim. Ardından z, z fonksiyonunun toplam artışı olarak adlandırılan bir artış alacaktır.), (yxfyyxxfz

M(x, y) noktasında f(x, y)'nin sürekli kısmi türevleri olduğunu varsayın.

Tanım. z \u003d f (x, y) fonksiyonunun 1. dereceden diferansiyeli, bu fonksiyonun toplam artışının Δ z ana kısmıdır, Δ x ve Δ y 'ye göre doğrusaldır, dz veya df sembolü ile gösterilir ve hesaplanır y y z x x z zd formülüyle

Bağımsız değişkenlerin diferansiyelleri artışlarıyla çakıştığı için, yani dx = Δ x , dy = Δ y , bu formül şu şekilde yazılabilir: dy y z dx x z zd

İki değişkenli f (x, y) bir fonksiyonun (x 0, y 0) noktasındaki toplam diferansiyelinin geometrik anlamı, geçiş sırasında teğet düzlemin yüzeye uygulamasının (z-koordinatı) artışıdır. (x 0, y 0) noktasından (x 0 + x, y 0 + y) noktasına.

İki değişkenli bir fonksiyonun toplam diferansiyelinin geometrik anlamı, bir değişkenli bir fonksiyonun diferansiyelinin geometrik anlamının uzamsal bir benzeridir.

Bir z \u003d f (x, y) fonksiyonunun 2. mertebeden diferansiyeli, 1. mertebeden diferansiyelinin diferansiyelidir ve gösterilir) (zzddd

z \u003d f (x, y) işlevinin 2. mertebesinin tüm kısmi türevleri sürekli ise, formül gerçekleşir: 2 2 2 y y z yx yx z x x z zdddd

Misal. y x yz 2 x fonksiyonunun 1. ve 2. mertebelerinin diferansiyellerini bulun

Karar. 1. ve 2. mertebelerin kısmi türevlerini bulun: y yx x z 1 2 2 2 y x x y z

; 202 1 2 2 2 yy y xy xx z cy ; 1 2 2 2 y xy yyx z cx 33 22 22 2)2(0 y x yx y x x y y z cy

Bu nedenle 1. ve 2. mertebelerin diferansiyelleri şöyle yazılacaktır: dy y x xdx y xyz)() 1 2(d 2 2 2 32 222) 1 2(22 y y x yx y xxyzdddd

f(x, y) fonksiyonu (x, y) noktasında türevlenebilir olsun. Bu fonksiyonun toplam artışını bulalım :), (yxfyyxxfz zyxfyyxxf), (

Bu formüle bir ifade koyarsak, yaklaşık bir formül elde ederiz: y yf x xf dzz y y yxf x x yxf yyxxf), (

Misal. Fonksiyonun x = 1, y = 2, z = 102, 1 ln 04, 1 99, 1 zxu y ln'deki değerine dayalı olarak yaklaşık bir değer hesaplayın

Karar. Verilen ifadeden x \u003d 1, 04 - 1 \u003d 0.04, y \u003d 1.99 - 2 \u003d -0.01, z \u003d 1.02 - 1 \u003d 0.02'yi belirliyoruz. u (x, y, z) = 11 ln

Kısmi türevleri bulun: 1 12 12 ln 2 1 zx xy x u y y 0 ln 2 ln zx xx y u y y

u fonksiyonunun toplam diferansiyeli: 2 1 ln 2 1 zx z z u y

05, 001, 004, 0 02, 0 21 01, 0004, 01 02, 001, 004, 0 zu yu xudu

Bu ifadenin tam değeri şudur: 1, 049275225687319176. 05, 105, 01)1, 2, 1(02, 1 ln 04, 1 99, 1 duu

Yüzeye M 0 noktasındaki teğet düzlemi, bu noktadan yüzey üzerine çizilen eğrilerin tüm teğetlerini içeren düzlemdir.

M 0 noktasındaki yüzeyin normali, bu noktadan geçen ve verilen noktada çizilen teğet düzleme dik olan düz çizgidir.

Yüzey F (x, y, z) \u003d 0 denklemi ile verilirse, M 0 (x 0, y 0, z 0) noktasındaki teğet düzlemin denklemi şu şekildedir: 0)) ( (00 0000 zz. MF yy. MFxx. MF z yx

M 0 (x 0 , y 0 , z 0) noktasında yüzeye çizilen normalin denklemleri aşağıdaki gibi yazılacaktır:)()()(0 0 0 MF zz MF yy MF xx zyx

Yüzey z \u003d f (x, y) denklemi ile verilirse, M 0 (x 0, y 0, z 0) noktasındaki teğet düzlemin denklemi :)) (, (000) 0000 yyyxf xxyxfzz y x

ve normal denklemler aşağıdaki gibi yazılacaktır: 1), (0 00 0 zz yxf yy yxf xx yx

Misal. 01332 22 yzxzxyyx ise M 0 (x 0, y 0, z 0) noktasında teğet düzlemi ve yüzeyin normalinin denklemlerini oluşturun. 1, 200yx

Karar. Yüzey denklemine x 0 ve y 0 koyarak, z 0 değerini buluruz: buradan z 0 = 1'i buluruz. Bu nedenle, M 0 (2, - 1, 1) temas noktasıdır. 01)1(32)1(23)1(2400 2zz

Problemin durumuna göre, yüzey örtük olarak verilmiştir. M 0 (2, – 1, 1) : 1332), (22 yzxzxyyxzyx) noktasındaki kısmi türevleri gösteriniz ve bulunuz.

, 32 zyx. F x 21)1(322)(0 MF x , 334 zxy.F y 51323)1(4)(0 MF y , 3 yx. F z 1)1(32)(0 MF z

Kısmi türevlerin bulunan değerlerini teğet düzlem 0'ın denkleminde değiştiririz))((00 0000 zz. MF yy. MFxx. MF z yx)

Normal denklemler 1 1 5 1 2 2 zyx biçimindedir.

Tanım. z = f (x , y) fonksiyonu M 0 (x 0 , y 0) noktasında bir maksimuma sahiptir, eğer bu noktanın böyle bir komşuluğu varsa, bu komşuluktan herhangi bir M (x , y) noktası için eşitsizlik geçerlidir ), (00 yxfyxf

Bir fonksiyon verilsin. x ve y bağımsız değişkenler olduğundan biri değişebilirken diğeri değişmeden kalabilir. y'nin değerini değiştirmeden bağımsız değişken x'i artıralım. Daha sonra z, z'nin x'e göre kısmi artışı olarak adlandırılan ve ile gösterilen bir artış alacaktır. Böyle, .

Benzer şekilde, y'ye göre z'de kısmi bir artış elde ederiz: .

z fonksiyonunun toplam artışı eşitlik tarafından belirlenir.

Bir limit varsa, fonksiyonun x değişkenine göre noktadaki kısmi türevi olarak adlandırılır ve sembollerden biri ile gösterilir:

Bir noktada x'e göre kısmi türevler genellikle sembollerle gösterilir. .

'nin y değişkenine göre kısmi türevi benzer şekilde tanımlanır ve gösterilir:

Bu nedenle, birkaç (iki, üç veya daha fazla) değişkenli bir fonksiyonun kısmi türevi, kalan bağımsız değişkenlerin değerlerinin sabitliğine tabi olarak, bu değişkenlerden birinin bir fonksiyonunun türevi olarak tanımlanır. Bu nedenle, bir fonksiyonun kısmi türevleri, bir değişkenli bir fonksiyonun türevlerini hesaplamak için formüllere ve kurallara göre bulunur (bu durumda, sırasıyla x veya y, sabit bir değer olarak kabul edilir).

Kısmi türevlere birinci dereceden kısmi türevler de denir. fonksiyonları olarak kabul edilebilirler. Bu fonksiyonlar, ikinci dereceden kısmi türevler olarak adlandırılan kısmi türevlere sahip olabilir. Bunlar aşağıdaki gibi tanımlanır ve gösterilir:

; ;

; .

İki değişkenli bir fonksiyonun 1. ve 2. mertebesinin diferansiyelleri.

Bir fonksiyonun (formül 2.5) toplam diferansiyeline birinci dereceden diferansiyel denir.

Toplam diferansiyelin hesaplanması için formül aşağıdaki gibidir:

(2.5) veya , nerede ,

fonksiyonun kısmi diferansiyelleri .

Fonksiyonun ikinci mertebeden sürekli kısmi türevleri olsun. İkinci mertebeden diferansiyel formül tarafından belirlenir. Bulalım:

Buradan: . Sembolik olarak şöyle yazılır:

BELİRSİZ ENTEGRAL.

Bir fonksiyonun ters türevi, belirsiz integral, özellikler.

F(x) işlevi çağrılır ilkel belirli bir f(x) fonksiyonu için, eğer F"(x)=f(x) ise veya aynısı, eğer dF(x)=f(x)dx ise.

Teorem. Sonlu veya sonsuz uzunlukta bir (X) aralığında tanımlanan bir f(x) fonksiyonunun bir ters türevi, F(x) varsa, o zaman aynı zamanda sonsuz sayıda ters türevi vardır; hepsi F(x)+C ifadesinde bulunur, burada C isteğe bağlı bir sabittir.

Belirli bir f(x) fonksiyonu için belirli bir aralıkta veya sonlu veya sonsuz uzunluktaki bir segmentte tanımlanan tüm ters türevlerin kümesine denir. belirsiz integral f(x) fonksiyonundan [veya f(x)dx ] ifadesinden ve sembolü ile gösterilir.

F(x), f(x'in ters türevlerinden biriyse, o zaman ters türev teoremi ile

, burada C keyfi bir sabittir.

Ters türevin tanımına göre, F "(x)=f(x) ve bu nedenle, dF(x)=f(x) dx. Formül (7.1), f(x) integral olarak adlandırılır ve f( x) dx, integral ifadesi olarak adlandırılır.

Üç değişkenli bir fonksiyonun ikinci dereceden kısmi türevlerini bulmanın genel ilkesi, iki değişkenli bir fonksiyonun ikinci dereceden kısmi türevlerini bulma ilkesine benzer.

İkinci mertebeden kısmi türevleri bulmak için önce birinci mertebeden kısmi türevleri bulmalısınız veya başka bir gösterimde:

İkinci mertebeden dokuz kısmi türev vardır.

Birinci grup, aynı değişkenlere göre ikinci türevlerdir:

Veya - "x"e göre ikinci türev;

Veya - "y"ye göre ikinci türev;

Veya - "z"ye göre ikinci türev.

İkinci grup ise karışık 2. dereceden kısmi türevler, bunlardan altı tane var:

Veya - karışık"x y'ye göre" türevi;

Veya - karışık"y x'e göre" türevi;

Veya - karışık"x z'ye göre" türevi;

Veya - karışık"po zet x" türevi;

Veya - karışık"Z oyununa göre" türevi;

Veya - karışık türevi "po z y".

İki değişkenli bir fonksiyon durumunda olduğu gibi, problem çözerken, ikinci dereceden karışık türevlerin aşağıdaki eşitliklerine odaklanılabilir:

Not: Açıkçası, bu her zaman böyle değildir. Karışık türevlerin eşitliği için süreklilik şartının yerine getirilmesi gerekmektedir.

Her ihtimale karşı, bu rezaletin yüksek sesle nasıl okunacağına dair birkaç örnek:

- "y'de iki kez iki vuruş";

- “de iki y po de zet meydanı”;

- “z üzerinde x üzerinde iki vuruş”;

- "iki y po de z po de y".

Örnek 10

Üç değişkenli bir fonksiyon için tüm birinci ve ikinci mertebeden kısmi türevleri bulun:

Karar:İlk olarak, birinci dereceden kısmi türevleri buluyoruz:

Bulunan türevi alıyoruz

ve "y" ile ayırt edin:

Bulunan türevi alıyoruz

ve onu "x" ile ayırt edin:

Eşitlik yapılır. İyi.

İkinci karışık türev çifti ile ilgileniyoruz.

Bulunan türevi alıyoruz

ve "z" ile ayırt edin:

Bulunan türevi alıyoruz

ve onu "x" ile ayırt edin:

Eşitlik yapılır. İyi.

Benzer şekilde, üçüncü karışık türev çifti ile ilgileniyoruz:

Eşitlik yapılır. İyi.

Yapılan çalışmadan sonra, birinci mertebeden tüm kısmi türevleri doğru bir şekilde bulduğumuz, ikinci olarak da 2. mertebeden karışık kısmi türevleri de doğru bir şekilde bulduğumuz garanti edilebilir.

İkinci mertebeden üç kısmi türev daha bulmak için kalır, burada hatalardan kaçınmak için mümkün olduğunca konsantre olmalısınız:

Hazır. Yine, görev hacimli olduğu kadar zor değil. Çözüm kısaltılabilir ve karışık kısmi türevlerin eşitlikleri olarak adlandırılabilir, ancak bu durumda doğrulama yapılmayacaktır. Bu yüzden zaman ayırıp bulmak daha iyi Tümü türevler (ayrıca, bu öğretmen tarafından istenebilir) veya aşırı durumlarda bir taslağı kontrol edin.

Örnek 11

Üç değişkenli bir fonksiyon için tüm birinci ve ikinci mertebeden kısmi türevleri bulun

Bu bir kendin yap örneğidir.

Çözümler ve cevaplar:

Örnek 2:Karar:

Örnek 4:Karar: Birinci mertebeden kısmi türevleri bulalım.

Birinci mertebenin toplam diferansiyelini oluşturuyoruz:

Örnek 6:Karar: M(1, -1, 0):

Örnek 7:Karar: noktasında birinci mertebeden kısmi türevleri hesaplayalım.M(1, 1, 1):

Örnek 9:Karar:

Örnek 11:Karar: Birinci mertebeden kısmi türevleri bulalım:

İkinci mertebeden kısmi türevleri bulalım:

integraller

8.1. Belirsiz integral. Detaylı Çözüm Örnekleri

konuyu incelemeye başlayalım Belirsiz integral" ve ayrıca en basit (ve tam olarak değil) integrallerin çözüm örneklerini ayrıntılı olarak analiz edin. Her zamanki gibi, kendimizi sayısız ders kitabında bulunan minimum teori ile sınırlayacağız, görevimiz integrallerin nasıl çözüleceğini öğrenmek.

Malzemede başarılı bir şekilde ustalaşmak için bilmeniz gerekenler nelerdir? İntegral hesabı ile başa çıkabilmek için, en azından ortalama düzeyde türevleri bulabilmeniz gerekir. Arkanızda birkaç düzine veya daha iyisi, bağımsız olarak bulunan yüzlerce türeviniz varsa, bu gereksiz bir deneyim olmayacaktır. En azından, en basit ve en yaygın işlevleri ayırt etme görevi sizi şaşırtmamalıdır.

Görünüşe göre, makaledeki integrallerden bahsediyorsak, türevler nerede ?! Ve işte olay. Gerçek şu ki, türev bulma ve belirsiz integral bulma (farklılaşma ve entegrasyon), toplama/çıkarma veya çarpma/bölme gibi birbirinin tersi olan iki eylemdir. Bu nedenle, türev bulma konusunda bir beceri ve bir tür deneyim olmadan, ne yazık ki, daha fazla ilerleyemez.

Bu bağlamda, aşağıdaki metodolojik materyallere ihtiyacımız olacak: türev tablosu ve integral tablosu.

Belirsiz integralleri çalışmanın zorluğu nedir? Türevlerde kesinlikle 5 farklılaşma kuralı, bir türev tablosu ve oldukça açık bir eylem algoritması varsa, o zaman integrallerde her şey farklıdır. Onlarca entegrasyon yöntemi ve tekniği var. Ve, entegrasyon yöntemi başlangıçta yanlış seçilmişse (yani, nasıl çözüleceğini bilmiyorsanız), o zaman integral, çeşitli hileleri ve püf noktalarını fark etmeye çalışırken, gerçek bir bilmece gibi, kelimenin tam anlamıyla günlerce “deliklenebilir”. . Hatta bazıları bundan hoşlanıyor.

Bu arada, öğrencilerden (beşeri bilimlerden değil) sık sık şöyle bir görüş duyduk: “Limit veya türevi çözmekle hiç ilgilenmedim, ancak integraller tamamen farklı bir konudur, heyecan verici, her zaman “ crack "karmaşık bir integral" . Durmak. Yeter kara mizah, hadi bu çok belirsiz integrallere geçelim.

Çözmenin birçok yolu olduğuna göre, bir çaydanlık belirsiz integralleri incelemeye nereden başlar? İntegral hesapta, bize göre, her şeyin etrafında döndüğü üç sütun veya bir tür "eksen" vardır. Her şeyden önce, en basit integralleri iyi anlamalısınız (bu makale).

O zaman dersi ayrıntılı olarak çalışmanız gerekir. BU EN ÖNEMLİ RESEPSİYON! İntegrallere ayrılmış tüm makalelerin belki de en önemli makalesi. Üçüncüsü, mutlaka okuyun Parçalara göre entegrasyon, çünkü geniş bir işlev sınıfını bütünleştirir. En azından bu üç derste ustalaşırsanız, zaten “iki değil” vardır. Bilmediğin için affedebilirsin trigonometrik fonksiyonların integralleri, kesirlerin integralleri, kesirli rasyonel fonksiyonların integralleri, irrasyonel fonksiyonların integralleri (kökler), ancak değiştirme yönteminde veya parça yöntemiyle entegrasyonda “bir su birikintisine girerseniz”, çok, çok kötü olacaktır.

Öyleyse, basit başlayalım. İntegral tablosuna bakalım. Türevlerde olduğu gibi, birkaç integrasyon kuralı ve bazı temel fonksiyonların bir integral tablosunu görüyoruz. Herhangi bir tablo integrali (ve aslında herhangi bir belirsiz integral) şu şekildedir:

Doğrudan gösterime ve terimlere geçelim:

- ayrılmaz simgesi.

- integrand işlevi ("s" harfiyle yazılmıştır).

– diferansiyel simgesi. Ne olduğunu, çok yakında ele alacağız. Ana şey, integrali yazarken ve çözüm sırasında bu simgeyi kaybetmemek önemlidir. Gözle görülür bir kusur olacaktır.

integralin integrali veya "doldurulmasıdır".

– ters türev işlev.

– . Terimlerle çok yüklenmeye gerek yok, buradaki en önemli şey, herhangi bir belirsiz integralde cevaba bir sabit eklenmesidir.

Belirsiz bir integrali çözmek içinters türev fonksiyonlar seti verilen integralden

Girişe tekrar bir göz atalım:

İntegral tablosuna bakalım.

Ne oluyor? sol taraflarımız dönüyorlar diğer işlevler için: .

Tanımımızı basitleştirelim:

Belirsiz integrali çözün - onu belirsiz (sabite kadar) bir fonksiyona DÖNÜŞTÜRMEK anlamına gelir , bazı kurallar, teknikler ve bir tablo kullanarak.

Örneğin, tablo integralini alın . Ne oldu? Sembolik kayıt, bir dizi ters türev fonksiyonuna dönüşmüştür.

Türevlerde olduğu gibi, integrallerin nasıl bulunacağını öğrenmek için teorik açıdan integralin veya ters türev fonksiyonun ne olduğunun farkında olmak gerekli değildir. Sadece bazı biçimsel kurallara göre dönüşümler yapmak yeterlidir. Yani, durumda integralin neden tam olarak dönüştüğünü anlamak hiç de gerekli değildir. Bunu ve diğer formülleri hafife alabilirsiniz. Herkes elektrik kullanır, ancak çok az insan elektronların teller boyunca nasıl hareket ettiğini düşünür.

Türev alma ve integrasyon zıt işlemler olduğundan, doğru bulunan herhangi bir ters türev için aşağıdakiler doğrudur:

Başka bir deyişle, doğru cevap türevlenirse, orijinal integralin elde edilmesi gerekir.

Aynı tablo integraline geri dönelim .

Bu formülün geçerliliğini doğrulayalım. Sağ tarafın türevini alıyoruz:

orijinal integraldir.

Bu arada, bir fonksiyona neden her zaman bir sabitin atandığı daha açık hale geldi. Türev alırken, bir sabit her zaman sıfıra dönüşür.

Belirsiz integrali çözün bulmak demektir bir demet Tümü antitürevler ve tek bir işlev değil. İncelenen tablo örneğinde, , , , vb. - tüm bu fonksiyonlar integralin çözümüdür. Sonsuz sayıda çözüm var, bu yüzden kısaca şöyle yazıyorlar:

Bu nedenle, herhangi bir belirsiz integralin kontrol edilmesi yeterince kolaydır. Bu, farklı türlerdeki çok sayıda integral için bir miktar telafidir.

Spesifik örneklere geçelim. Türev çalışmasında olduğu gibi, iki entegrasyon kuralıyla başlayalım:

- devamlı C integral işaretinden çıkarılabilir (ve alınmalıdır).

– iki fonksiyonun toplamının (farkının) integrali, iki integralin toplamına (farkının) eşittir. Bu kural herhangi bir sayıda terim için geçerlidir.

Gördüğünüz gibi, kurallar temelde türevlerle aynıdır. Bazen denir doğrusallık özellikleri integral.

örnek 1

Belirsiz integrali bulun.

Bir kontrol yapın.

Karar: Gibi dönüştürmek daha uygundur.

(1) Kuralın uygulanması . Diferansiyel simgesini yazmayı unutmayın dx her integralin altında. Neden her birinin altında? dxtam çarpanıdır. Ayrıntılı olarak boyarsanız, ilk adım aşağıdaki gibi yazılmalıdır:

(2) Kurala göre tüm sabitleri integrallerin işaretlerinden alıyoruz. Dikkat edin, son dönemde tg 5 bir sabittir, onu da çıkarırız.

Ayrıca bu adımda entegrasyon için kökleri ve dereceleri hazırlıyoruz. Farklılaşmada olduğu gibi, kökler formda temsil edilmelidir. . Paydada bulunan kökler ve dereceler - yukarı hareket ettirin.

Not: türevlerden farklı olarak, integrallerdeki köklerin her zaman forma indirgenmesi gerekmez ve dereceleri yukarı hareket ettirin.

Örneğin, - bu, sizden önce zaten hesaplanmış olan hazır bir tablo integralidir ve her türlü Çin hilesi gibi tamamen gereksiz. Benzer şekilde: - bu aynı zamanda bir tablo integralidir, formda bir kesri temsil etmenin bir anlamı yoktur . Tabloyu dikkatlice inceleyin!

(3) Tüm integraller tablo şeklindedir. Formülleri kullanarak tabloyu kullanarak dönüşümü gerçekleştiriyoruz: , ve

bir güç işlevi için - .

Tablo integralinin, bir güç fonksiyonu için formülün özel bir hali olduğuna dikkat edilmelidir: .

Devamlı C sadece ifadenin sonuna bir kez ekleyin

(onları her integralin arkasına koymak yerine).

(4) Elde edilen sonucu, formun tüm dereceleri olduğunda daha kompakt bir biçimde yazarız.

yine kökler olarak temsil edilir ve negatif üslü güçler paydaya geri sıfırlanır.

muayene Kontrolü gerçekleştirmek için alınan cevabı ayırt etmeniz gerekir:

İlk integrand, yani, integral doğru bulundu. Dans ettiklerinden buna döndüler. İntegrali olan hikayenin böyle bitmesi güzel.

Zaman zaman belirsiz integrali kontrol etmek için biraz farklı bir yaklaşım vardır, türev değil, ancak cevaptan diferansiyel alınır:

Sonuç olarak, bir integrant değil, bir integrant elde ederiz.

Diferansiyel kavramından korkmayın.

Diferansiyel, türev ile çarpımıdır dx.

Ancak, bizim için önemli olan teorik incelikler değil, bu farkla sonra ne yapılacağıdır. Diferansiyel şu şekilde ortaya çıkar: simge d kaldırın, parantezin sağına bir çizgi koyun, ifadenin sonuna bir çarpan atayın dx :

Alınan başlangıç integrand, yani integral doğru bulunmuştur.

Gördüğünüz gibi, diferansiyel türevi bulmaya geliyor. Daha az kontrol etmenin ikinci yolunu seviyorum, çünkü ek olarak büyük parantezler çizmem ve diferansiyel simgesini sürüklemem gerekiyor. dx testin sonuna kadar. Daha doğru veya "daha sağlam" veya başka bir şey olmasına rağmen.

Aslında, ikinci doğrulama yöntemi hakkında sessiz kalmak mümkündü. Mesele yöntemde değil, diferansiyeli açmayı öğrenmiş olmamızdır. Tekrar.

Diferansiyel aşağıdaki gibi ortaya çıkar:

1) simge d kaldırmak;

2) parantezin üzerine sağ tarafa bir vuruş koyun (türevin tanımı);

3) ifadenin sonunda bir faktör atarız dx .

Örneğin:

Hatırla bunu. Çok yakında düşünülen tekniğe ihtiyacımız olacak.

Örnek 2

Belirsiz bir integral bulduğumuzda, DAİMA kontrol etmeye çalışırız.Üstelik bunun için büyük bir fırsat var. Yüksek matematikteki tüm problem türleri bu bakış açısından bir hediye değildir. Kontrol görevlerinde genellikle doğrulamanın gerekli olmadığı önemli değildir, hiç kimse ve hiçbir şey taslak üzerinde yapılmasını engellemez. Bir istisna ancak yeterli zaman olmadığında yapılabilir (örneğin, testte, sınavda). Şahsen, her zaman integralleri kontrol ederim ve doğrulama eksikliğini bir hack ve eksik tamamlanmış bir görev olarak görüyorum.

Örnek 3

Belirsiz integrali bulun:

. Bir kontrol yapın.

Çözüm: İntegrali analiz ettiğimizde, integralin altında iki fonksiyonun çarpımına sahip olduğumuzu ve hatta tüm ifadeyi kuvvete yükselttiğimizi görüyoruz. Ne yazık ki, bütünleşik savaş alanında Numara iyi ve rahat çarpım ve bölümü entegre etmek için formüller gibi: veya .

Bu nedenle, bir çarpım veya bölüm verildiğinde, integrali toplamanın mümkün olup olmadığını görmek her zaman mantıklıdır? Dikkate alınan örnek, mümkün olduğu durumdur.

İlk önce tam çözümü veriyoruz, yorumlar aşağıda olacak.

(1) Herhangi bir gerçek sayı için eski güzel kare toplam formülünü kullanırız, ortak parantezin üzerindeki dereceden kurtuluruz. parantezlerin dışında ve kısaltılmış çarpma formülünü ters yönde uygulayarak: .

Örnek 4

belirsiz integrali bulun

Bir kontrol yapın.

Bu kendi kendine çözme için bir örnektir. Dersin sonunda cevaplayın ve çözümü tamamlayın.

Örnek 5

belirsiz integrali bulun

. Bir kontrol yapın.

Bu örnekte, integral bir kesirdir. İntegranda bir kesir gördüğümüzde ilk akla gelen soru şu olmalıdır: “Bu kesirden bir şekilde kurtulmak ya da en azından basitleştirmek mümkün müdür?”.

Paydanın yalnız bir "x" kökü içerdiğini fark ettik. Alandaki kişi bir savaşçı değil, yani payı payda terime göre terime bölebilirsiniz:

Bir fonksiyonun türeviyle ilgili makalelerde defalarca tartışıldığı için kesirli kuvvetlere sahip eylemler hakkında yorum yapmıyoruz.

Hala böyle bir örnekle kafanız karıştıysa

ve kimse doğru cevabı alamaz,

Ayrıca çözümün bir adımı atladığını, yani kuralların uygulandığını unutmayın. , . Genellikle, integralleri çözme konusunda belirli bir deneyime sahip olan bu kurallar, açık bir gerçek olarak kabul edilir ve ayrıntılı olarak açıklanmaz.

Örnek 6

Belirsiz integrali bulun. Bir kontrol yapın.

Bu kendi kendine çözme için bir örnektir. Dersin sonunda cevaplayın ve çözümü tamamlayın.

Genel durumda, integrallerdeki kesirler ile her şey o kadar basit değildir, makalede bazı türlerdeki kesirlerin entegrasyonu hakkında ek materyaller bulunabilir: Bazı kesirlerin integrali. Ancak, yukarıdaki makaleye geçmeden önce dersi okumanız gerekir: Belirsiz integralde yer değiştirme yöntemi. Gerçek şu ki, bir fonksiyonu diferansiyel veya değişken değiştirme yöntemi altında toplamak, kilit nokta Konunun incelenmesinde, yalnızca "değiştirme yöntemi için saf atamalarda" değil, aynı zamanda diğer birçok integral türünde de bulunduğundan.

Çözümler ve cevaplar:

Örnek 2: Çözüm:

Örnek 4: Çözüm:

Bu örnekte, indirgenmiş çarpma formülünü kullandık.

Örnek 6: Çözüm:

Belirsiz bir integralde bir değişkeni değiştirme yöntemi. Çözüm örnekleri

Bu derste, belirsiz integralleri çözme sürecinde kullanılan en önemli ve en yaygın hilelerden biri olan değişken yönteminin değiştirilmesi ile tanışacağız. Materyalde başarılı bir şekilde ustalaşmak için başlangıç bilgisi ve entegrasyon becerileri gereklidir. İntegral hesabında boş bir dolu çaydanlık hissi varsa, önce malzemeye aşina olmalısınız. Belirsiz integral. Çözüm örnekleri, burada integralin ne olduğu erişilebilir bir biçimde açıklanır ve yeni başlayanlar için temel örnekler ayrıntılı olarak analiz edilir.

Teknik olarak, belirsiz bir integralde bir değişkeni değiştirme yöntemi iki şekilde uygulanır:

– Fonksiyonu diferansiyelin işareti altına getirmek.

– Değişkenin gerçek değişimi.

Aslında aynı şey ama çözümün tasarımı farklı görünüyor. Daha basit bir durumla başlayalım.

Bu derste, iki değişkenli fonksiyon kavramını tanıyacağız ve ayrıca en yaygın görevi ayrıntılı olarak ele alacağız - bulma kısmi türevler birinci ve ikinci mertebeden, fonksiyonun toplam diferansiyeli.

Aşağıdaki materyali etkili bir şekilde incelemek için, gerekli Bir değişkenli bir fonksiyonun "olağan" türevlerini az çok güvenle bulabilir. Türevleri nasıl doğru bir şekilde ele alacağınızı derslerde öğrenebilirsiniz. Türev nasıl bulunur? ve Bileşik bir fonksiyonun türevi. Ayrıca, temel fonksiyonların türevleri tablosuna ve farklılaşma kurallarına da ihtiyacımız var, basılı biçimde el altındaysa en uygunudur.

İki değişkenli bir fonksiyon kavramıyla başlayalım, sitenin pratik bir odağı olduğu için kendimizi minimum teori ile sınırlamaya çalışacağız. İki değişkenli bir fonksiyon genellikle olarak yazılır ve değişkenler çağrılır. bağımsız değişkenler veya argümanlar.

Örnek: - iki değişkenli bir fonksiyon.

Bazen notasyon kullanılır. Harf yerine harfin kullanıldığı görevler de vardır.

Fonksiyonların geometrik anlamlarını bilmekte fayda var. Bir değişkenin işlevi, örneğin tanıdık okul parabolü gibi düzlemdeki belirli bir çizgiye karşılık gelir. Geometrik açıdan iki değişkenli herhangi bir fonksiyon, üç boyutlu uzayda bir yüzeydir (düzlemler, silindirler, toplar, paraboloidler, vb.). Ama aslında bu zaten analitik geometri ve gündemimizde matematiksel analiz var.

Birinci ve ikinci derecelerin kısmi türevlerini bulma sorununa dönüyoruz. Birkaç fincan kahve içmiş ve hayal edilemeyecek kadar zor malzeme havasında olanlar için iyi haberlerim var: kısmi türevler, tek değişkenli bir fonksiyonun "adi" türevleri ile hemen hemen aynıdır.

Kısmi türevler için tüm türev kuralları ve temel fonksiyonların türevleri tablosu geçerlidir. Şu anda öğreneceğimiz sadece birkaç küçük fark var.

örnek 1

Bir fonksiyonun birinci ve ikinci mertebesinin kısmi türevlerini bulun

İlk olarak, birinci dereceden kısmi türevleri buluyoruz. İki tane var.

Tanımlamalar:

Veya - "x"e göre kısmi türev

Veya - "y"ye göre kısmi türev

İle başlayalım .

Önemli! "x"e göre kısmi türevi bulduğumuzda, değişken sabit (sabit sayı) olarak kabul edilir.

Biz karar veririz. Bu dersimizde hemen tam çözümü vereceğiz ve aşağıda yorum yapacağız.

Alınan önlemlere ilişkin yorumlar:

(1) Kısmi türevi bulduğumuzda yaptığımız ilk şey şu sonuca varmaktır: Tümü tire altında parantez içinde işlev alt simge ile.

Dikkat önemli! Abonelikler çözüm sırasında KAYBETMEZ. Bu durumda, olmadan bir yere “vuruş” çizerseniz, öğretmen en azından onu görevin yanına koyabilir (dikkatsizlik için puanın hemen bir kısmını ısırır).

(2) Farklılaşma kurallarını kullanın ; . Bunun gibi basit bir örnek için, her iki kural da aynı adımda uygulanabilir. İlk terime dikkat edin: çünkü sabit kabul edilir ve türevin işaretinden herhangi bir sabit alınabilir., sonra parantez içinden çıkarıyoruz. Yani, bu durumda, normal bir sayıdan daha iyi değildir. Şimdi üçüncü terime bakalım: burada tam tersine çıkarılacak bir şey yok. Sabit olduğu için aynı zamanda bir sabittir ve bu anlamda son terim olan “yedi” den daha iyi değildir.

(2) Temel fonksiyonların türev tablosunu kullanıyoruz. Zihinsel olarak tablodaki tüm "X"leri "Y" olarak değiştirin. Yani, bu tablo aynı derecede geçerlidir. (ve genel olarak herhangi bir harf için). Bu durumda kullandığımız formüller: ve .

Böylece birinci mertebeden kısmi türevler bulunur.

Ve hiçbir şey aramanıza gerek yok: ayrı makalemizde, yapabilmeniz için zaten her şeyi hazırladık. Şimdi kısmi türevlerden bahsedelim.

Faydalı haber bültenleri ve güncel öğrenci haberleri için telegram kanalımıza hoş geldiniz.

İki veya daha fazla değişkenin işlevi

Kısmi türevlerden bahsetmeden önce, onsuz kısmi türevin anlamı olmayan birkaç değişkenli fonksiyon kavramına değinmemiz gerekiyor. Okulda, tek değişkenli fonksiyonlarla uğraşmaya alışkınız:

Bu tür fonksiyonların türevlerini daha önce ele almıştık. Bir değişkenin fonksiyonunun grafiği, bir düzlemdeki bir çizgidir: düz bir çizgi, bir parabol, bir hiperbol, vb.

Başka bir değişken eklersek ne olur? Bunun gibi bir işlev elde edersiniz:

Bu, iki bağımsız değişkenin bir fonksiyonudur. x ve y. Böyle bir fonksiyonun grafiği, üç boyutlu uzayda bir yüzeydir: bir küre, bir hiperboloid, bir paraboloid veya bir boşlukta başka bir küresel at. Kısmi türev fonksiyonları z sırasıyla x ve y için aşağıdaki gibi yazılır:

Üç veya daha fazla değişkenli fonksiyonlar da vardır. Doğru, böyle bir fonksiyonun grafiğini çizmek imkansızdır: bu, tasvir edilemeyen en az dört boyutlu alan gerektirir.

Birinci dereceden kısmi türev

Ana kuralı hatırla:

Değişkenlerden birine göre kısmi türev hesaplanırken ikinci değişken sabit olarak alınır. Aksi takdirde, türevi hesaplama kuralları değişmez.

Yani kısmi türev esasen normal olandan farklı değildir. Bu nedenle, temel fonksiyonların türevleri tablosunu ve sıradan türevleri hesaplama kurallarını gözünüzün önünde bulundurun. Bunu oldukça açık hale getirmek için bir örneğe bakalım. Aşağıdaki fonksiyonun birinci mertebeden kısmi türevlerini hesaplamak istediğinizi varsayalım:

İlk olarak, y'yi adi bir sayı olarak kabul ederek, x'e göre kısmi türevi alıyoruz:

Şimdi x'i sabit alarak y'ye göre kısmi türevi ele alalım:

Gördüğünüz gibi, bu konuda karmaşık bir şey yok ve daha karmaşık örneklerle başarı sadece bir uygulama meselesidir.

İkinci dereceden kısmi türev

İkinci mertebeden kısmi türev nedir? Tıpkı ilki gibi. İkinci mertebeden kısmi türevleri bulmak için, sadece birinci mertebeden türevin türevini almanız yeterlidir. Yukarıdaki örneğe dönelim ve ikinci mertebeden kısmi türevleri hesaplayalım.

Oyuna göre:

Üçüncü ve daha yüksek derecelerin kısmi türevleri, hesaplama ilkesinde farklılık göstermez. Kuralları düzenleyelim:

Bir bağımsız değişkene göre türev alırken, ikincisi sabit olarak alınır.
İkinci mertebeden türev, birinci mertebeden türevin türevidir. Üçüncü mertebe, ikinci mertebeden türevin türevidir, vb.

Bir fonksiyonun kısmi türevleri ve toplam diferansiyeli

Pratik görevlerde sıkça sorulan bir soru, bir fonksiyonun toplam diferansiyelini bulmaktır. Birkaç değişkenli bir fonksiyon için, toplam diferansiyel, argümanların artışlarına göre fonksiyonun küçük toplam artışının ana doğrusal kısmı olarak tanımlanır.

Tanım kulağa hantal geliyor, ancak harflerle her şey daha kolay. Birkaç değişkenli bir fonksiyonun toplam birinci mertebeden diferansiyeli şuna benzer:

Kısmi türevlerin nasıl hesaplandığını bilerek, toplam diferansiyelin hesaplanmasında sorun yoktur.

Kısmi türevler o kadar da gereksiz bir konu değildir. Örneğin, ikinci mertebeden kısmi diferansiyel denklemler, gerçek fiziksel süreçlerin matematiksel tanımı için yaygın olarak kullanılmaktadır.

Burada birinci ve ikinci mertebeden kısmi türevlerin sadece genel, yüzeysel bir fikrini verdik. Bu konuyla ilgileniyor musunuz veya özel sorularınız mı var? Yorumlarda onlara sorun ve eğitiminizde nitelikli ve hızlı yardım için profesyonel öğrenci servisinin uzmanlarıyla iletişime geçin. Bizimle sorunla yalnız kalmayacaksınız!