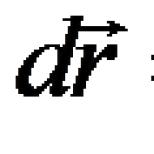Typy matíc a ich vlastnosti. Základné operácie s maticami. Definícia operácie násobenia dvoch matíc

Niektoré vlastnosti operácií s maticami.
Maticové výrazy

A teraz bude nasledovať pokračovanie témy, v ktorej zvážime nielen nový materiál, ale aj vypracujeme maticové operácie.

Niektoré vlastnosti operácií s maticami

Existuje pomerne málo vlastností, ktoré súvisia s operáciami s maticami, na tej istej Wikipédii môžete obdivovať štíhle rady zodpovedajúcich pravidiel. V praxi sú však mnohé vlastnosti v určitom zmysle „mŕtve“, keďže len niektoré z nich sa využívajú pri riešení skutočných problémov. Mojím cieľom je pozrieť sa na aplikáciu vlastností na konkrétnych príkladoch a ak potrebujete rigoróznu teóriu, použite iný zdroj informácií.

Zvážte niektoré výnimky z pravidla potrebné na vykonávanie praktických úloh.

Ak má štvorcová matica inverzná matica, potom je ich násobenie komutatívne:

matica identity sa nazýva štvorcová matica s hlavná uhlopriečka jednotky sú umiestnené a zvyšné prvky sa rovnajú nule. Napríklad: atď.

V čom nasledujúca vlastnosť je pravdivá: ak sa vynásobí ľubovoľná matica ľavá alebo pravá pomocou matice identity vhodných veľkostí, výsledkom je pôvodná matica:

Ako vidíte, prebieha tu aj komutatívnosť násobenia matíc.

Vezmime si nejakú maticu, povedzme maticu z predchádzajúceho problému: .

Záujemcovia si môžu skontrolovať a uistiť sa, že:

Identitná matica pre matice je analógom numerickej jednotky pre čísla, čo je obzvlášť jasne vidieť z práve uvažovaných príkladov.

Komutativita číselného faktora vzhľadom na násobenie matíc

Nasledujúca vlastnosť platí pre matice a reálne čísla:

To znamená, že číselný faktor sa môže (a mal by) posunúť dopredu, aby „nezasahoval“ do násobiacich matíc.

Poznámka : Vo všeobecnosti je znenie vlastnosti neúplné - "lambda" môže byť umiestnená kdekoľvek medzi maticami, dokonca aj na konci. Pravidlo zostáva v platnosti, ak sa násobia tri alebo viac matíc.

Príklad 4

Vypočítajte produkt

rozhodnutie:

(1) Podľa majetku posunúť číselný faktor dopredu. Samotné matrice nie je možné preskupovať!

(2) - (3) Vykonajte násobenie matice.

(4) Tu môžete rozdeliť každé číslo 10, ale potom sa medzi prvkami matice objavia desatinné zlomky, čo nie je dobré. Všimli sme si však, že všetky čísla v matici sú deliteľné 5, takže každý prvok vynásobíme .

Odpoveď:

Malá šaráda, ktorú musíte vyriešiť sami:

Príklad 5

Vypočítajte, ak

Riešenie a odpoveď na konci hodiny.

Aká technika je dôležitá pri riešení takýchto príkladov? Zaobchádzanie s číslami posledný .

K lokomotíve pripojíme ďalší vagón:

Ako vynásobiť tri matice?

V prvom rade, ČO by malo byť výsledkom vynásobenia troch matíc? Mačka neporodí myš. Ak je násobenie matice možné, výsledkom bude tiež matica. No, môj učiteľ algebry nevidí, ako vysvetľujem uzavretosť algebraickej štruktúry vzhľadom na jej prvky =)

Súčin troch matíc možno vypočítať dvoma spôsobmi:

1) nájdite a potom vynásobte maticou "ce": ;

2) buď najskôr nájdite a potom vykonajte násobenie.

Výsledky sa budú nevyhnutne zhodovať a teoreticky táto vlastnosť sa nazýva asociativita násobenia matíc:

Príklad 6

Vynásobte matice dvoma spôsobmi

Algoritmus riešenia dvojkrokový: nájdite súčin dvoch matíc, potom opäť nájdite súčin dvoch matíc.

1) Použite vzorec

Akcia jedna:

Akcia dva:

2) Použite vzorec

Akcia jedna:

Akcia dva:

Odpoveď:

Známejší a štandardnejší je samozrejme prvý spôsob riešenia, tam „akoby všetko bolo v poriadku“. Mimochodom, o objednávke. V uvažovanej úlohe často vzniká ilúzia, že hovoríme o nejakej permutácii matíc. Nie sú tu. Znovu ti to pripomínam všeobecne NEVYMEŇUJTE MATICE. Takže v druhom odseku, v druhom kroku, vykonáme násobenie, ale v žiadnom prípade. S obyčajnými číslami by takéto číslo prešlo, ale s maticami nie.

Vlastnosť asociatívnosti násobenia platí nielen pre štvorcové, ale aj pre ľubovoľné matice - ak sa len násobia:

Príklad 7

Nájdite súčin troch matíc

Toto je príklad „urob si sám“. Vo vzorovom riešení boli výpočty uskutočnené dvoma spôsobmi, analyzovať, ktorý spôsob je ziskovejší a kratší.

Vlastnosť asociatívnosti násobenia matíc prebieha pre väčší počet faktorov.

Teraz je čas vrátiť sa k silám matíc. Štvorec matice sa zvažuje na samom začiatku a na programe je otázka:

Ako kockovať maticu a vyššie mocniny?

Tieto operácie sú tiež definované len pre štvorcové matice. Ak chcete zvýšiť štvorcovú maticu na kocku, musíte vypočítať súčin:

V skutočnosti ide o špeciálny prípad násobenia troch matíc podľa asociatívnej vlastnosti násobenia matíc: . A matica vynásobená sama osebe je druhou mocninou matice:

Tak dostaneme pracovný vzorec:

To znamená, že úloha sa vykonáva v dvoch krokoch: najprv sa musí matica odmocniť a potom sa výsledná matica vynásobí maticou.

Príklad 8

Zdvihnite maticu na kocku.

Toto je malý problém, ktorý musíte vyriešiť sami.

Zvýšenie matice na štvrtú mocninu sa vykonáva prirodzeným spôsobom:

Pomocou asociativity násobenia matíc odvodíme dva pracovné vzorce. Prvý: je súčinom troch matíc.

jeden) . Inými slovami, najprv nájdeme, potom to vynásobíme „byť“ - dostaneme kocku a nakoniec znova vykonáme násobenie - bude štvrtý stupeň.

2) Existuje však riešenie o krok kratšie: . To znamená, že v prvom kroku nájdeme štvorec a obídeme kocku a vykonáme násobenie

Dodatočná úloha k príkladu 8:

Zdvihnite maticu na štvrtú mocninu.

Ako už bolo uvedené, možno to urobiť dvoma spôsobmi:

1) Akonáhle je kocka známa, vykonáme násobenie.

2) Ak je však podľa stavu problému potrebné zostaviť maticu len na štvrtom stupni, potom je výhodné cestu skrátiť - nájsť druhú mocninu matice a použiť vzorec .

Obe riešenia aj odpoveď sú na konci lekcie.

Podobne je matica povýšená na piatu a vyššiu mocninu. Z praktických skúseností môžem povedať, že niekedy sú príklady povýšenia na 4. stupeň, ale už si nepamätám niečo z piateho stupňa. Ale pre každý prípad uvediem optimálny algoritmus:

1) nájsť;
2) nájsť;
3) zdvihnite maticu na piatu mocninu: .

Tu sú snáď všetky hlavné vlastnosti maticových operácií, ktoré môžu byť užitočné pri praktických problémoch.

V druhej časti lekcie sa očakáva nemenej pestrá párty.

Maticové výrazy

Zopakujme si zaužívané školské výrazy s číslami. Číselný výraz pozostáva z čísel, matematických symbolov a zátvoriek, napríklad: . Vo výpočtoch platí známa algebraická priorita: po prvé, zátvorkách, potom vykonaný umocňovanie / extrakcia koreňov, po násobenie / delenie a naposledy - sčítanie / odčítanie.

Ak má číselný výraz zmysel, tak výsledkom jeho vyhodnotenia je číslo, Napríklad:

Maticové výrazy takmer presne to isté! S tým rozdielom, že hlavnými aktérmi sú matrice. Plus niektoré špecifické maticové operácie, ako je transpozícia a nájdenie inverznej matice.

Zvážte maticový výraz , kde su nejake matrice. Tento maticový výraz má tri členy a operácie sčítania/odčítania sa vykonávajú ako posledné.

V prvom termíne musíte najskôr transponovať maticu "be": , potom vykonať násobenie a pridať "dve" k výslednej matici. poznač si to operácia transponovania má vyššiu prioritu ako operácia násobenia. Zátvorky, rovnako ako v číselných výrazoch, menia poradie akcií: - tu sa najprv vykoná násobenie, potom sa výsledná matica transponuje a vynásobí 2.

V druhom termíne sa najskôr vykoná násobenie matice a inverzná matica sa už nájde z produktu. Ak sú zátvorky odstránené: , musíte najprv nájsť inverznú maticu a potom vynásobiť matice: . Nájdenie inverznej matice má tiež prednosť pred násobením.

Pri treťom člene je všetko zrejmé: maticu zdvihneme do kocky a do výslednej matice pridáme „päťku“.

Ak má maticový výraz zmysel, tak výsledkom jeho vyhodnotenia je matica.

Všetky úlohy budú zo skutočných testov a začneme tým najjednoduchším:

Príklad 9

Maticové údaje . Nájsť:

rozhodnutie: poradie operácií je zrejmé, najskôr sa vykoná násobenie, potom sčítanie.

Sčítanie nie je možné, pretože matice majú rôzne veľkosti.

Nečudujte sa, v úlohách tohto typu sa často ponúkajú očividne nemožné akcie.

Skúsme vypočítať druhý výraz:

Všetko je tu v poriadku.

Odpoveď: akcia sa nedá vykonať, .

Matrice. Akcie na matrice. Vlastnosti operácií s maticami. Typy matríc.

Matice (a podľa toho aj matematická časť - maticová algebra) sú dôležité v aplikovanej matematike, keďže umožňujú pomerne jednoduchou formou písať významnú časť matematických modelov objektov a procesov. Termín "matrix" sa objavil v roku 1850. Matrice boli prvýkrát spomenuté v starovekej Číne, neskôr arabskými matematikmi.

Matrix A = Amn objednávka m*n sa volá obdĺžniková tabuľka čísel obsahujúca m - riadkov a n - stĺpcov.

Maticové prvky aij, pre ktoré i=j sa nazývajú uhlopriečka a tvar hlavná uhlopriečka.

Pre štvorcovú maticu (m=n) je hlavná uhlopriečka tvorená prvkami a 11 , a 22 ,..., a nn .

Maticová rovnosť.

A = B, ak matica nariadi A a B sú rovnaké a a ij =b ij (i=1,2,...,m; j=1,2,...,n)

Akcie na matrice.

1. Sčítanie matice - operácia po prvkoch

2. Odčítanie matice - operácia prvok po prvku

3. Súčin matice číslom je operácia po jednotlivých prvkoch

4. Násobenie A*B matice podľa pravidla riadok na stĺpec(počet stĺpcov matice A sa musí rovnať počtu riadkov matice B)

A mk *B kn = C mn a každý prvok s ij matice Cmn sa rovná súčtu súčinov prvkov i-teho riadku matice A zodpovedajúcimi prvkami j-tého stĺpca matice B, t.j.

Ukážme si operáciu násobenia matíc na príklade

5. Umocňovanie

m>1 je kladné celé číslo. A je štvorcová matica (m=n), t.j. relevantné len pre štvorcové matice

6. Transpozícia matice A. Transponovaná matica je označená A T alebo A "

Riadky a stĺpce sú vymenené

Príklad

Vlastnosti operácií s maticami

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(λA)"=λ(A)"

(A+B)"=A"+B"

(AB)"=B"A"

Typy matríc

1. Obdĺžnikový: m a n- ľubovoľné kladné celé čísla

2. Štvorec: m=n

3. Riadok matice: m = 1. Napríklad (1 3 5 7) - v mnohých praktických problémoch sa takáto matica nazýva vektor

4. Maticový stĺpec: n=1. napríklad

5. Diagonálna matica: m=n a a ij = 0, ak i≠j. napríklad

6. Matica identity: m=n a

7. Nulová matica: a ij = 0, i = 1,2,...,m

j=1,2,...,n

8. Trojuholníková matica: všetky prvky pod hlavnou uhlopriečkou sú 0.

9. Symetrická matica: m=n a aij=aji(t.j. na miestach, ktoré sú symetrické vzhľadom na hlavnú uhlopriečku, sú rovnaké prvky), a preto A"=A

Napríklad,

10. Šikmá matica: m=n a a ij =-a ji(t.j. protiľahlé prvky stoja na miestach, ktoré sú symetrické vzhľadom na hlavnú uhlopriečku). Preto sú na hlavnej uhlopriečke nuly (pretože pri i=j máme a ii =-a ii)

To je jasné, A"=-A

11. Hermitovská matica: m=n a a ii =-ã ii (ã ji- komplexný - konjugovaný s a ji, t.j. ak A = 3+2i, potom komplexný konjugát A=3-2i)

V tomto článku pochopíme, ako sa vykonáva operácia sčítania na maticách rovnakého rádu, operácia násobenia matice číslom a operácia násobenia matíc vhodného rádu, axiomaticky nastavíme vlastnosti operácií, a tiež diskutovať o priorite operácií na matriciach. Paralelne s teóriou uvedieme podrobné riešenia príkladov, v ktorých sa vykonávajú operácie s maticami.

Hneď si všimneme, že všetko nasledujúce platí pre matice, ktorých prvkami sú reálne (alebo komplexné) čísla.

Navigácia na stránke.

Operácia sčítania dvoch matíc.

Definícia operácie sčítania dvoch matíc.

Operácia sčítania je definovaná LEN PRE MATICE ROVNAKÉHO PORADIA. Inými slovami, je nemožné nájsť súčet matíc rôznych rozmerov a vo všeobecnosti nemožno hovoriť o sčítaní matíc rôznych rozmerov. Tiež sa nedá hovoriť o súčte matice a čísla alebo o súčte matice a nejakého iného prvku.

Definícia.

Súčet dvoch matíc a je maticou, ktorej prvky sa rovnajú súčtu zodpovedajúcich prvkov matíc A a B, teda .

Výsledkom operácie sčítania dvoch matíc je teda matica rovnakého rádu.

Vlastnosti operácie sčítania matrice.

Aké sú vlastnosti operácie sčítania matice? Na túto otázku je celkom ľahké odpovedať, vychádzajúc z definície súčtu dvoch matíc daného rádu a zapamätania si vlastností operácie sčítania reálnych (alebo komplexných) čísel.

1. Pre matice A, B a C rovnakého rádu je vlastnosť asociatívnosti sčítania charakteristická A + (B + C) \u003d (A + B) + C.
2. Pre matice daného rádu existuje neutrálny prvok vzhľadom na sčítanie, ktorým je nulová matica. To znamená, že vlastnosť A + O \u003d A je pravdivá.
3. Pre nenulovú maticu A daného rádu existuje matica (-A), ich súčet je nulová matica: A + (-A) \u003d O .
4. Pre matice A a B daného rádu platí vlastnosť komutativity sčítania A+B=B+A.

V dôsledku toho množina matíc daného rádu generuje aditívnu Abelovu grupu (Abelovu grupu vzhľadom na algebraickú operáciu sčítania).

Maticové sčítanie – riešenie príkladov.

Pozrime sa na niekoľko príkladov sčítania matice.

Príklad.

Nájdite súčet matíc a .

rozhodnutie.

Poradie matíc A a B sú rovnaké a rovné 4 x 2, takže môžeme vykonať operáciu sčítania matíc a výsledkom by mala byť matica poriadku 4 x 2. Podľa definície operácie sčítania dvoch matíc vykonáme sčítanie prvok po prvku:

Príklad.

Nájdite súčet dvoch matíc a ktorých prvkami sú komplexné čísla.

rozhodnutie.

Keďže poradie matíc sú rovnaké, môžeme vykonať sčítanie.

Príklad.

Vykonajte sčítanie troch matíc .

rozhodnutie.

Najprv pridajte maticu A s B, potom pridajte C k výslednej matici:

Máme nulovú maticu.

Operácia násobenia matice číslom.

Definícia operácie násobenia matice číslom.

Operácia násobenia matice číslom je definovaná PRE MATICE AKÉHOKOĽVEK PORADIA.

Definícia.

Súčin matice a reálneho (alebo komplexného) čísla je matica, ktorej prvky sa získajú vynásobením zodpovedajúcich prvkov pôvodnej matice číslom, teda .

Výsledkom vynásobenia matice číslom je teda matica rovnakého rádu.

Vlastnosti operácie násobenia matice číslom.

Z vlastností operácie násobenia matice číslom vyplýva, že vynásobením nulovej matice nulou vznikne nulová matica a súčin ľubovoľného čísla a nulovej matice je nulová matica.

Násobenie matice číslom - príklady a ich riešenie.

Poďme sa zaoberať operáciou násobenia matice číslom na príkladoch.

Príklad.

Nájdite súčin čísla 2 a matice .

rozhodnutie.

Ak chcete vynásobiť maticu číslom, musíte vynásobiť každý jej prvok týmto číslom:

Príklad.

Vykonajte násobenie matice číslom.

rozhodnutie.

Každý prvok danej matice vynásobíme daným číslom:

Operácia násobenia dvoch matíc.

Definícia operácie násobenia dvoch matíc.

Operácia násobenia dvoch matíc A a B je definovaná len pre prípad, keď sa POČET STĹPCOV MATICE A ROVNÁ POČTU RIADKOV MATICE B.

Definícia.

Súčin matice A rádu a matice B rádu- ide o takú maticu C rádu, ktorej každý prvok sa rovná súčtu súčinov prvkov i-tého riadku matice A zodpovedajúcimi prvkami j-tého stĺpca matice B, tj. ,

Výsledkom operácie násobenia matice objednávok maticou objednávok je teda matica objednávok.

Násobenie matice maticou - riešenia príkladov.

Násobením matíc sa budeme zaoberať na príkladoch, po ktorých prejdeme k vypisovaniu vlastností operácie násobenia matíc.

Príklad.

Nájdite všetky prvky matice C, ktorá sa získa vynásobením matíc a .

rozhodnutie.

Poradie matice A je p=3 x n=2, poradie matice B je n=2 x q=4, takže poradie súčinu týchto matíc je p=3 x q=4. Použime vzorec

Postupne berieme hodnoty i od 1 do 3 (keďže p=3 ) pre každé j od 1 do 4 (keďže q=4 ), a n=2 v našom prípade, potom

Takto sa vypočítajú všetky prvky matice C a matica získaná vynásobením dvoch daných matíc má tvar .

Príklad.

Vykonajte násobenie matice a .

rozhodnutie.

Poradie pôvodných matíc nám umožňuje vykonať operáciu násobenia. V dôsledku toho by sme mali dostať maticu poradia 2 x 3.

Príklad.

Dané matice a . Nájdite súčin matíc A a B, ako aj matíc B a A.

rozhodnutie.

Keďže poradie matice A je 3 x 1 a matice B je 1 x 3, potom A⋅B bude mať poradie 3 x 3 a súčin matíc B a A bude mať poradie 1 x 1.

Ako môžeš vidieť, . Toto je jedna z vlastností operácie násobenia matice.

Vlastnosti operácie násobenia matíc.

Ak sú matice A, B a C vhodného usporiadania, potom platí nasledovné vlastnosti operácie násobenia matíc.

Treba poznamenať, že pre vhodné objednávky súčin nulovej matice O a matice A dáva nulovú maticu. Súčin A a O tiež dáva nulovú maticu, ak objednávky umožňujú operáciu násobenia matíc.

Medzi štvorcovými maticami sa nachádzajú tzv permutačné matice, operácia násobenia je pre nich komutatívna, teda . Príkladom permutačných matíc je pár matice identity a akejkoľvek inej matice rovnakého rádu, pretože .

Priorita operácií na matriciach.

Operácie násobenia matice číslom a násobenia matice maticou majú rovnakú prioritu. Zároveň majú tieto operácie vyššiu prioritu ako operácia sčítania dvoch matíc. Najprv sa teda matica vynásobí číslom a matice sa vynásobia a až potom sa matice sčítajú. Poradie, v ktorom sú operácie vykonávané na maticiach, však možno špecifikovať explicitne pomocou zátvoriek.

Takže priorita operácií s maticami je podobná priorite priradenej operáciám sčítania a násobenia reálnych čísel.

Príklad.

Maticové údaje . Vykonajte zadané akcie s danými maticami .

rozhodnutie.

Začneme vynásobením matice A maticou B:

Teraz vynásobíme maticu identity E druhého rádu dvoma:

Pridáme dve výsledné matice:

Zostáva vykonať operáciu vynásobenia výslednej matice maticou A:

Treba poznamenať, že operácia odčítania matíc rovnakého rádu A a B ako taká neexistuje. Rozdiel dvoch matíc je v podstate súčet matice A a matice B predbežne vynásobený mínusom jedna: .

Operácia zvýšenia štvorcovej matice na prirodzenú mocninu tiež nie je nezávislá, pretože ide o postupné násobenie matíc.

Zhrnúť.

Na množine matíc sú definované tri operácie: sčítanie matíc rovnakého rádu, násobenie matice číslom a násobenie matíc vhodných rádov. Operácia sčítania na množine matíc daného rádu generuje Abelovu skupinu.

Matrice. Typy matríc. Operácie s maticami a ich vlastnosti.

Determinant matice n-tého rádu. N, Z, Q, R, C,

Matica rádu m*n je obdĺžniková tabuľka čísel, ktorá obsahuje m-riadkov a n-stĺpcov.

Maticová rovnosť:

Dve matice sa nazývajú rovnaké, ak sa počet riadkov a stĺpcov jednej z nich rovná počtu riadkov a stĺpcov druhej matice, resp. prvky týchto matíc sú rovnaké.

Poznámka: Prvky s rovnakými indexmi sú spárované.

Typy matríc:

Štvorcová matica: Matica sa nazýva štvorcová, ak sa počet riadkov rovná počtu stĺpcov.

Obdĺžnikový: O matici sa hovorí, že je obdĺžniková, ak sa počet riadkov nerovná počtu stĺpcov.

Riadková matica: matica rádu 1*n (m=1) má tvar a11,a12,a13 a nazýva sa riadková matica.

Maticový stĺpec: ………….

Uhlopriečka: uhlopriečka štvorcovej matice prechádzajúca z ľavého horného rohu do pravého dolného rohu, to znamená, že pozostáva z prvkov a11, a22 ...... - sa nazýva hlavná uhlopriečka. (definícia: štvorcová matica, ktorej všetky prvky sa rovnajú nule, okrem tých, ktoré sa nachádzajú na hlavnej uhlopriečke, sa nazýva diagonálna matica.

Identita: Diagonálna matica sa nazýva identita, ak sú všetky prvky umiestnené na hlavnej diagonále a sú rovné 1.

Horný trojuholník: A=||aij|| sa nazýva horná trojuholníková matica, ak aij=0. Za predpokladu, že i>j.

Dolný trojuholník: aij=0. i

Nula: Toto je matica, ktorej Els sú 0.

Operácie na matriciach.

1. Transpozícia.

2. Násobenie matice číslom.

3. Sčítanie matice.

4. Maticové násobenie.

Základné pôsobenie sv-va na matice.

1.A+B=B+A (komutativity)

2.A+(B+C)=(A+B)+C (asociativita)

3.a(A+B)=aA+aB (distributivita)

4.(a+b)A=aA+bA (distributívna)

5.(ab)A=a(bA)=b(aA) (asoots.)

6.AB≠BA (bez komunikácie)

7.A(BC)=(AB)C (asociatívne) – vykoná sa, ak def. Vykonávajú sa produkty Matrix.

8.A(B+C)=AB+AC (distributívna)

(B+C)A=BA+CA (distributívna)

9.a(AB)=(aA)B=(aB)A

Determinant štvorcovej matice - definícia a jeho vlastnosti. Rozklad determinantu v riadkoch a stĺpcoch. Metódy výpočtu determinantov.

Ak má matica A rád m>1, potom determinantom tejto matice je číslo.

Algebraický doplnok Aij prvku aij matice A je vedľajšia Mij vynásobená číslom

VĚTA 1: Determinant matice A sa rovná súčtu súčinov všetkých prvkov ľubovoľného riadku (stĺpca) a ich algebraických doplnkov.

Základné vlastnosti determinantov.

1. Determinant matice sa pri jej transpozícii nezmení.

2. Pri permutácii dvoch riadkov (stĺpcov) determinant zmení znamienko, ale jeho absolútna hodnota sa nemení.

3. Determinant matice, ktorá má dva rovnaké riadky (stĺpce), je 0.

4. Pri vynásobení riadku (stĺpca) matice číslom sa jej determinant vynásobí týmto číslom.

5. Ak jeden z riadkov (stĺpcov) matice pozostáva z 0, potom determinant tejto matice je 0.

6. Ak sú všetky prvky i-tého riadku (stĺpca) matice reprezentované ako súčet dvoch členov, potom jej determinant môže byť reprezentovaný ako súčet determinantov dvoch matíc.

7. Determinant sa nezmení, ak sa prvky jedného stĺpca (riadku) pridajú k prvkom druhého stĺpca (riadku) vopred vynásobené. za rovnaké číslo.

8. Súčet ľubovoľných prvkov ľubovoľného stĺpca (riadka) determinantu k príslušnému algebraickému doplnku prvkov iného stĺpca (riadka) je 0.

https://pandia.ru/text/78/365/images/image004_81.gif" width="46" height="27">

Metódy na výpočet determinantu:

1. Podľa definície alebo vety 1.

2. Redukcia na trojuholníkový tvar.

Definícia a vlastnosti inverznej matice. Výpočet inverznej matice. Maticové rovnice.

Definícia: Štvorcová matica rádu n sa nazýva inverzná matica A rovnakého rádu a označuje sa

Aby matica A mala inverznú maticu, je potrebné a postačujúce, aby determinant matice A bol odlišný od 0.

Vlastnosti inverznej matice:

1. Jedinečnosť: pre danú maticu A je jej inverzná hodnota jedinečná.

2. maticový determinant

3. Operácia transpozície a inverznej matice.

Maticové rovnice:

Nech A a B sú dve štvorcové matice rovnakého rádu.

https://pandia.ru/text/78/365/images/image008_56.gif" width="163" height="11 src=">

Koncept lineárnej závislosti a nezávislosti stĺpcov matice. Vlastnosti lineárnej závislosti a lineárnej nezávislosti stĺpcového systému.

Stĺpce А1,А2…An sa nazývajú lineárne závislé, ak existuje ich netriviálna lineárna kombinácia rovná 0. stĺpcu.

Stĺpce А1,А2…An sa nazývajú lineárne nezávislé, ak existuje ich netriviálna lineárna kombinácia rovná 0. stĺpcu.

Lineárna kombinácia sa nazýva triviálna, ak sa všetky koeficienty С(l) rovnajú 0 a inak netriviálna.

https://pandia.ru/text/78/365/images/image010_52.gif" width="88" height="24">

2. Aby boli stĺpce lineárne závislé, je potrebné a postačujúce, aby niektorý stĺpec bol lineárnou kombináciou iných stĺpcov.

Nech je 1 zo stĺpcov https://pandia.ru/text/78/365/images/image014_42.gif" width="13" height="23 src="> lineárnou kombináciou iných stĺpcov.

https://pandia.ru/text/78/365/images/image016_38.gif" width="79" height="24"> sú lineárne závislé, potom sú lineárne závislé všetky stĺpce.

4. Ak je systém stĺpcov lineárne nezávislý, potom ktorýkoľvek z jeho podsystémov je tiež lineárne nezávislý.

(Všetko, čo sa hovorí o stĺpcoch, platí aj pre riadky).

Matrix maloletí. Základ maloletých. Poradie matice. Metóda obmedzovania neplnoletých osôb na výpočet hodnosti matice.

Menší rád matice A je determinant, ktorého prvky sa nachádzajú v priesečníku k-riadkov a k-riadkov matice A.

Ak sú všetky minority rádu k matice A = 0, potom každá minorita rádu k + 1 sa tiež rovná 0.

Základné moll.

Hodnosť matice A je rádovo menší.

Spôsob ohraničenia neplnoletých osôb: - Vyberáme nenulový prvok matice A (ak takýto prvok neexistuje, potom hodnosť A \u003d 0)

Predchádzajúcu moll 1. rádu ohraničujeme moll 2. rádu. (Ak tento maloletý nie je rovný 0, potom hodnosť >=2) Ak je hodnosť tohto neplnoletého =0, tak vybraného maloletého 1. rádu ohraničíme s ostatnými maloletými 2. rádu. (Ak všetci maloletí 2. rádu = 0, potom poradie matice = 1).

Poradie matice. Metódy zisťovania hodnosti matice.

Hodnosť matice A je rádovo menší.

Metódy výpočtu:

1) Metóda ohraničenia maloletých: -Vyberte nenulový prvok matice A (ak taký prvok nie je, potom poradie =0) - Ohraničte predchádzajúci vedľajší prvok 1. rádu vedľajším prvkom 2. rádu..gif" width="40 " height="22" >r+1 Mr+1=0.

2) Prevedenie matice do stupňovitého tvaru: táto metóda je založená na elementárnych transformáciách. Pri elementárnych transformáciách sa poradie matice nemení.

Nasledujúce transformácie sa nazývajú elementárne transformácie:

Permutácia dvoch riadkov (stĺpcov).

Násobenie všetkých prvkov niektorého stĺpca (riadka) číslom nie =0.

Pridanie ku všetkým prvkom určitého stĺpca (riadku) prvkov iného stĺpca (riadku), predtým vynásobené rovnakým číslom.

Základná vedľajšia veta. Nevyhnutná a postačujúca podmienka, aby sa determinant rovnal nule.

Základom minor matice A je minorita najväčšieho k-tého rádu odlišného od 0.

Základná vedľajšia veta:

Základné riadky (stĺpce) sú lineárne nezávislé. Ľubovoľný riadok (stĺpec) matice A je lineárnou kombináciou základných riadkov (stĺpcov).

Poznámky: Riadky a stĺpce, na ktorých priesečníku je základná vedľajšia, sa nazývajú základné riadky a stĺpce.

a11 a12… a1r a1j

a21 a22...a2r a2j

a31 a32...a3r a3j

ar1 ar2 ….arr arj

ak1 ak2…..akr akj

Nevyhnutné a postačujúce podmienky na to, aby sa determinant rovnal nule:

Aby bol determinant n-tého rádu = 0, je potrebné a postačujúce, aby jeho riadky (stĺpce) boli lineárne závislé.

Sústavy lineárnych rovníc, ich klasifikácia a formy zápisu. Cramerovo pravidlo.

Uvažujme systém 3 lineárnych rovníc s tromi neznámymi:

https://pandia.ru/text/78/365/images/image020_29.gif" alt="(!LANG:l14image048" width="64" height="38 id=">!}

sa nazýva determinant systému.

Ďalšie tri determinanty poskladáme takto: postupne nahradíme 1, 2 a 3 stĺpce v determinante D stĺpcom voľných členov

https://pandia.ru/text/78/365/images/image022_23.gif" alt="(!LANG:l14image052" width="93" height="22 id=">!}

Dôkaz. Uvažujme teda o systéme 3 rovníc s tromi neznámymi. 1. rovnicu systému vynásobíme algebraickým doplnkom A11 prvku a11, 2. rovnicu A21 a 3. rovnicu A31:

https://pandia.ru/text/78/365/images/image024_24.gif" alt="(!LANG:l14image056" width="247" height="31 id=">!}

Zvážte každú zo zátvoriek a pravú stranu tejto rovnice. Podľa vety o expanzii determinantu z hľadiska prvkov 1. stĺpca

https://pandia.ru/text/78/365/images/image026_23.gif" alt="(!LANG:l14image060" width="324" height="42 id=">!}

Podobne možno ukázať, že a .

Nakoniec je ľahké to vidieť

Dostaneme teda rovnosť: .

Preto, .

Rovnosti a sú odvodené podobne, odkiaľ nasleduje tvrdenie vety.

Sústavy lineárnych rovníc. Podmienka kompatibility pre lineárne rovnice. Kronecker-Capelliho veta.

Riešením sústavy algebraických rovníc je taká množina n čísel C1,C2,C3……Cn, ktorá po dosadení do pôvodnej sústavy na miesto x1,x2,x3…..xn otočí všetky rovnice systém do identít.

Systém lineárnych algebraických rovníc sa nazýva konzistentný, ak má aspoň jedno riešenie.

Spoločný systém sa nazýva určitý, ak má jedinečné riešenie, a neurčitý, ak má nekonečne veľa riešení.

Podmienky kompatibility sústav lineárnych algebraických rovníc.

a11 a12 ……a1n x1 b1

a21 a22 ……a2n x2 b2

……………….. .. = ..

am1 am2....amn xn bn

VETA: Aby bol systém m lineárnych rovníc s n neznámymi konzistentný, je potrebné a postačujúce, aby sa hodnosť rozšírenej matice rovnala hodnosti matice A.

Poznámka: Táto veta poskytuje iba kritériá pre existenciu riešenia, ale nenaznačuje spôsob, ako nájsť riešenie.

10 otázka.

Sústavy lineárnych rovníc. Metóda basic minor je všeobecná metóda na nájdenie všetkých riešení systémov lineárnych rovníc.

A=a21 a22....a2n

Základná vedľajšia metóda:

Nech je systém konzistentný a RgA=RgA’=r. Nech je v ľavom hornom rohu matice A namaľovaný základný moll.

https://pandia.ru/text/78/365/images/image035_20.gif" width="22" height="23 src=">…...gif" width="23" height="23 src= ">…...gif" width="22" height="23 src=">…...gif" width="46" height="23 src=">-…..-a

d2 b2-a(2r+1)x(r+1)-..-a(2n)x(n)

… = …………..

Dr br-a(rr+1)x(r+1)-..-a(rn)x(n)

https://pandia.ru/text/78/365/images/image050_12.gif" width="33" height="22 src=">

Poznámky: Ak sa poradie hlavnej a uvažovanej matice rovná r=n, potom v tomto prípade dj=bj a systém má jedinečné riešenie.

Homogénne sústavy lineárnych rovníc.

Systém lineárnych algebraických rovníc sa nazýva homogénny, ak sa všetky jeho voľné členy rovnajú nule.

AX=0 je homogénny systém.

AX = B je nehomogénny systém.

Homogénne systémy sú vždy kompatibilné.

X1 =x2 =..=xn =0

Veta 1.

Homogénne systémy majú nehomogénne riešenia, keď je poradie matice systému menšie ako počet neznámych.

Veta 2.

Homogénna sústava n-lineárnych rovníc s n-neznámymi má nenulové riešenie, keď sa determinant matice A rovná nule. (detA=0)

Vlastnosti roztokov homogénnych systémov.

Akákoľvek lineárna kombinácia riešenia homogénneho systému je sama o sebe riešením tohto systému.

a1C1 + a2C2; α1 a α2 sú nejaké čísla.

A(α1C1 + α2C2) = A(α1C1) + A(α2C2) = α1(A C1) + α2(AC2) = 0, t.j. k (AC1) = 0; (AC2) = 0

Pre nehomogénny systém táto vlastnosť neplatí.

Základný rozhodovací systém.

Veta 3.

Ak je rad maticového systému rovnice s n-neznámymi r, potom má tento systém n-r lineárne nezávislých riešení.

Nechajte základnú moll v ľavom hornom rohu. Ak r< n, то неизвестные х r+1;хr+2;..хn называются свободными переменными, а систему уравнений АХ=В запишем, как Аr Хr =Вr

C1 = (C11 C21 .. Cr1 , 1.0..0)

C2 = (C21 C22 .. C2r,0, 1..0)<= Линейно-независимы.

……………………..

Cn-r = (Cn-r1 Cn-r2 .. Cn-rr ,0, 0..1)

Systém n-r lineárne nezávislých riešení homogénnej sústavy lineárnych rovníc s n-neznámymi stupňami r sa nazýva fundamentálny systém riešení.

Veta 4.

Akékoľvek riešenie systému lineárnych rovníc je lineárnou kombináciou riešenia základného systému.

С = α1C1 + α2C2 + .. + αn-r Cn-r

Ak r

12 otázka.

Všeobecné riešenie nehomogénneho systému.

Spánok (gener. nejednotný) \u003d COO + SCH (súkromné)

AX=B (heterogénny systém); AX = 0

(ASoo) + ASch = ASch = B, pretože (ASoo) = 0

Spánok \u003d α1C1 + α2C2 + .. + αn-r Cn-r + Stred

Gaussova metóda.

Ide o metódu postupnej eliminácie neznámych (premenných) - spočíva v tom, že pomocou elementárnych transformácií sa pôvodná sústava rovníc redukuje na ekvivalentnú sústavu stupňovitého tvaru, z ktorej sa postupne zisťujú všetky ostatné premenné. , počnúc poslednými premennými.

Nech a≠0 (ak to tak nie je, potom sa to dosiahne preskupením rovníc).

1) vylúčime premennú x1 z druhej, tretej ... n-tej rovnice, pričom prvú rovnicu vynásobíme vhodnými číslami a získané výsledky pripočítame k 2., 3. ... n-tej rovnici, potom dostaneme:

Dostaneme systém ekvivalentný pôvodnému.

2) vylúčiť premennú x2

3) vylúčime premennú x3 atď.

Pokračujúc v procese postupnej eliminácie premenných x4;x5...xr-1 dostaneme pre (r-1)-tý krok.

Číslo nula posledného n-r v rovniciach znamená, že ich ľavá strana vyzerá takto: 0x1 +0x2+..+0xn

Ak sa aspoň jedno z čísel вr+1, вr+2… nerovná nule, potom je zodpovedajúca rovnosť nekonzistentná a systém (1) nie je konzistentný. Pre každý konzistentný systém sa teda vr+1 … vm rovná nule.

Posledných n-r rovníc v systéme (1;r-1) sú identity a možno ich ignorovať.

Možné sú dva prípady:

a) počet rovníc systému (1; r-1) sa rovná počtu neznámych, t.j. r \u003d n (v tomto prípade má systém trojuholníkový tvar).

b)r

Prechod zo systému (1) do ekvivalentného systému (1; r-1) sa nazýva priamy pohyb Gaussovej metódy.

O nájdení premennej zo systému (1; r-1) - opačným priebehom Gaussovej metódy.

Gaussove transformácie sa pohodlne vykonávajú tak, že sa neimplementujú pomocou rovníc, ale s rozšírenou maticou ich koeficientov.

13 otázka.

podobné matrice.

Budeme uvažovať iba štvorcové matice rádu n/

O matici A sa hovorí, že je podobná matici B (A~B), ak existuje nesingulárna matica S, takže A=S-1BS.

Vlastnosti podobných matíc.

1) Matica A je podobná sama sebe. (A~A)

Ak S=E, potom EAE=E-1AE=A

2) Ak A~B, potom B~A

Ak A=S-1BS => SAS-1= (SS-1)B(SS-1)=B

3) Ak A~B a súčasne B~C, potom A~C

Vzhľadom na to, že A=S1-1BS1 a B=S2-1CS2 => A= (S1-1 S2-1) C(S2 S1) = (S2 S1)-1C(S2 S1) = S3-1CS3, kde S3 = S2S1

4) Determinanty podobných matíc sú rovnaké.

Vzhľadom na to, že A~B, je potrebné dokázať, že detA=detB.

A=S-1 BS, detA=det(S-1 BS)= detS-1* detB* detS = 1/detS *detB*detS (znížiť) = detB.

5) Hodnosti podobných matríc sú rovnaké.

Vlastné vektory a vlastné hodnoty matíc.

Číslo λ sa nazýva vlastná hodnota matice A, ak existuje nenulový vektor X (stĺpec matice), takže AX = λ X, vektor X sa nazýva vlastný vektor matice A a súčet všetkých vlastných hodnôt sa nazýva spektrum matice A.

Vlastnosti vlastných vektorov.

1) Keď vynásobíme vlastný vektor číslom, dostaneme vlastný vektor s rovnakou vlastnou hodnotou.

AX \u003d λ X; Х≠0

α X => A (α X) \u003d α (AX) \u003d α (λ X) \u003d \u003d λ (α X)

2) Vlastné vektory s párovo odlišnými vlastnými hodnotami sú lineárne nezávislé λ1, λ2,.. λk.

Nech sa systém skladá z 1. vektora, urobme indukčný krok:

C1 X1 + C2 X2 + .. + Cn Xn = 0 (1) - vynásobte A.

C1 AX1 + C2 AX2 + .. + Cn AXn \u003d 0

С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn = 0

Vynásobte λn+1 a odčítajte

C1 X1 +C2 X2 + .. +Cn Xn+ Cn+1 Xn+1 = 0

С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn+ Сn+1 λn+1 Хn+1 = 0

C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn + Cn+1 (λn+1 –λn+1)Xn+1 = 0

C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn = 0

Je potrebné, aby C1 \u003d C2 \u003d ... \u003d Cn \u003d 0

Cn+1 Xn+1 λn+1 =0

Charakteristická rovnica.

A-λE sa nazýva charakteristická matica pre maticu A.

Na to, aby nenulový vektor X bol vlastným vektorom matice A, zodpovedajúcej vlastnej hodnote λ, je potrebné, aby bol riešením homogénnej sústavy lineárnych algebraických rovníc (A - λE)X = 0

Systém má netriviálne riešenie, keď det (A - XE) = 0 - to je charakteristická rovnica.

Vyhlásenie!

Charakteristické rovnice podobných matíc sa zhodujú.

det(S-1AS - λЕ) = det(S-1AS - λ S-1ЕS) = det(S-1 (A - λЕ)S) = det S-1 det(A - λЕ) detS= det(A - λЕ)

Charakteristický polynóm.

det(A – λЕ) - funkcia vzhľadom na parameter λ

det(A – λЕ) = (-1)n Xn +(-1)n-1(a11+a22+..+ann)λn-1+..+detA

Tento polynóm sa nazýva charakteristický polynóm matice A.

Dôsledok:

1) Ak sú matice A~B, tak súčet ich diagonálnych prvkov je rovnaký.

a11+a22+..+ann = в11+в22+..+вnn

2) Množina vlastných hodnôt podobných matíc sa zhoduje.

Ak sú charakteristické rovnice matíc rovnaké, nemusia byť nevyhnutne podobné.

Pre maticu A

Pre maticu B

https://pandia.ru/text/78/365/images/image062_10.gif" width="92" height="38">

Det(Ag-λE) = (λ11 – λ)(λ22 – λ)…(λnn – λ)= 0

Aby bola matica A rádu n diagonalizovaná, je potrebné, aby existovali lineárne nezávislé vlastné vektory matice A.

Dôsledok.

Ak sú všetky vlastné hodnoty matice A odlišné, potom je diagonalizovaná.

Algoritmus na hľadanie vlastných vektorov a vlastných hodnôt.

1) zostavte charakteristickú rovnicu

2) nájdite korene rovníc

3) zostavte sústavu rovníc na určenie vlastného vektora.

λi (A-λi E)X = 0

4) nájsť základný systém riešení

x1,x2..xn-r, kde r je poradie charakteristickej matice.

r = Rg(A - λi E)

5) vlastný vektor, vlastné hodnoty λi sú zapísané ako:

X \u003d C1 X1 + C2 X2 + .. + Cn-r Xn-r, kde C12 + C22 + ... C2n ≠0

6) skontrolujeme, či je možné maticu zmenšiť do diagonálneho tvaru.

7) nájdite Ag

Ag = S-1AS S=

15 otázka.

Základ priamky, roviny, priestoru.

https://pandia.ru/text/78/365/images/image065_9.gif" height="11">│, ││). Modul vektora je nula, keď je tento vektor nula (│ō│=0)

4. Orth vektor.

Orth daného vektora je vektor, ktorý má rovnaký smer ako daný vektor a má modul rovný jednej.

Rovnaké vektory majú rovnaké orty.

5. Uhol medzi dvoma vektormi.

Ide o menšiu časť plochy, ktorá je ohraničená dvoma lúčmi vychádzajúcimi z rovnakého bodu a smerujúcimi rovnakým smerom ako dané vektory.

Sčítanie vektorov. Násobenie vektora číslom.

1) Sčítanie dvoch vektorov

https://pandia.ru/text/78/365/images/image065_9.gif" height="11">+ │≤│ │+│ │

2) Násobenie vektora skalárom.

Súčin vektora a skaláru je nový vektor, ktorý má:

a) = súčin modulu vynásobeného vektora absolútnou hodnotou skaláru.

b) smer je rovnaký ako vynásobený vektor, ak je skalár kladný, a opačný, ak je skalár záporný.

λ a(vektor)=>│ λ │= │ λ │=│ λ ││ │

Vlastnosti lineárnych operácií s vektormi.

1. Zákon o komunite.

2. Zákon asociativity.

3. Sčítanie s nulou.

a(vektor)+ō= a(vektor)

4. Sčítanie s opakom.

5. (αβ) = α(β) = β(α)

6;7.Zákon distributivity.

Vyjadrenie vektora v zmysle jeho modulu a jednotkového vektora.

Maximálny počet lineárne nezávislých vektorov sa nazýva báza.

Základom na priamke je ľubovoľný nenulový vektor.

Základom v rovine sú ľubovoľné dva nekalenárne vektory.

Základom v priestore je systém ľubovoľných troch nekoplanárnych vektorov.

Koeficient expanzie vektora v nejakej báze nazývame zložky alebo súradnice vektora v danej báze.

https://pandia.ru/text/78/365/images/image075_10.gif" height="11 src=">.gif" height="11 src="> vykonať sčítanie a násobenie skalárom, potom ako výsledkom je ľubovoľný počet takýchto akcií, ktoré dostaneme:

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> sa nazývajú lineárne závislé, ak existuje ich netriviálna lineárna kombinácia rovná ō.

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> sa nazývajú lineárne nezávislé, ak neexistuje ich netriviálna lineárna kombinácia.

Vlastnosti lineárne závislých a nezávislých vektorov:

1) systém vektorov obsahujúci nulový vektor je lineárne závislý.

λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> sú lineárne závislé, niektorý vektor musí byť lineárnou kombináciou iných vektorov.

3) ak sú niektoré z vektorov zo systému a1 (vektor), a2 (vektor) ... ak (vektor) lineárne závislé, potom sú lineárne závislé všetky vektory.

4) ak sú všetky vektory https://pandia.ru/text/78/365/images/image076_9.gif" height="11 src=">.gif" width="75" height="11">

https://pandia.ru/text/78/365/images/image082_10.gif" height="11 src=">.gif" height="11 src=">)

Lineárne operácie v súradniciach.

https://pandia.ru/text/78/365/images/image069_9.gif" height="12 src=">.gif" height="11 src=">.gif" height="11 src="> .gif" height="11 src=">.gif" width="65" height="13 src=">

Vlastnosti bodového produktu:

1. Komutatívnosť

3. (a;b)=0 práve vtedy, ak sú vektory ortogonálne alebo ktorýkoľvek z vektorov je rovný 0.

4. Distributivita (αa+βb;c)=α(a;c)+β(b;c)

5. Vyjadrenie skalárneho súčinu aab z hľadiska ich súradníc

https://pandia.ru/text/78/365/images/image093_8.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image095_8.gif" width="254" height="13 src=">

Keď je podmienka () , h, l=1,2,3

https://pandia.ru/text/78/365/images/image098_7.gif" width="176" height="21 src=">

https://pandia.ru/text/78/365/images/image065_9.gif" height="11"> a volá sa tretí vektor, ktorý spĺňa nasledujúce rovnice:

3. - správne

Vlastnosti vektorového produktu:

4. Vektorový súčin súradnicových vektorov

ortonormálny základ.

https://pandia.ru/text/78/365/images/image109_7.gif" width="41" height="11 src=">

https://pandia.ru/text/78/365/images/image111_8.gif" width="41" height="11 src=">

Na označenie ort ortonormálneho základu sa často používajú 3 symboly

https://pandia.ru/text/78/365/images/image063_10.gif" width="77" height="11 src=">

https://pandia.ru/text/78/365/images/image114_5.gif" width="549" height="32 src=">

Ak je ortonormálny základ, potom

https://pandia.ru/text/78/365/images/image117_5.gif" width="116" height="15">- rovnica priamej rovnobežnej osi OX

2) - rovnica priamky rovnobežnej s osou OS

2. Vzájomné usporiadanie 2 rovných čiar.

Veta 1 Nech sú rovnice priamok dané vzhľadom na afinný súradnicový systém

A) Potom nevyhnutná a postačujúca podmienka, keď sa pretínajú, je:

B) Nevyhnutnou a postačujúcou podmienkou skutočnosti, že čiary sú rovnobežné, je podmienka:

B) Potom nevyhnutnou a postačujúcou podmienkou na to, aby sa riadky spojili do jednej, je podmienka:

3. Vzdialenosť od bodu k priamke.

Veta. Vzdialenosť od bodu k priamke vzhľadom na kartézsky súradnicový systém:

https://pandia.ru/text/78/365/images/image127_7.gif" width="34" height="11 src=">

4. Uhol medzi dvoma priamymi čiarami. Kolmý stav.

Nech sú dané 2 priame čiary vzhľadom na kartézsky súradnicový systém všeobecnými rovnicami.

https://pandia.ru/text/78/365/images/image133_4.gif" width="103" height="11 src=">

Ak , potom sú čiary kolmé.

24 otázka.

rovina vo vesmíre. Podmienka komponarity pre vektor a rovinu. Vzdialenosť od bodu k rovine. Podmienka rovnobežnosti a kolmosti dvoch rovín.

1. Podmienka komponarity pre vektor a rovinu.

https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image140.jpg" alt="(!LANG:Untitled4.jpg" width="111" height="39">!}

https://pandia.ru/text/78/365/images/image142_6.gif" width="86" height="11 src=">

https://pandia.ru/text/78/365/images/image144_6.gif" width="148" height="11 src=">

https://pandia.ru/text/78/365/images/image145.jpg" alt="(!LANG:Untitled5.jpg" width="88" height="57">!}

https://pandia.ru/text/78/365/images/image147_6.gif" width="31" height="11 src=">

https://pandia.ru/text/78/365/images/image148_4.gif" width="328" height="24 src=">

3. Uhol medzi 2 rovinami. Kolmý stav.

https://pandia.ru/text/78/365/images/image150_6.gif" width="132" height="11 src=">

Ak , potom sú roviny kolmé.

25 otázka.

Rovná čiara v priestore. Rôzne typy rovníc priamky v priestore.

https://pandia.ru/text/78/365/images/image156_6.gif" width="111" height="19">

2. Vektorová rovnica priamky v priestore.

https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src=">

https://pandia.ru/text/78/365/images/image162_5.gif" width="44" height="29 src=">

4. Kanonická rovnica je priama.

https://pandia.ru/text/78/365/images/image164_4.gif" width="34" height="18 src=">

https://pandia.ru/text/78/365/images/image166_0.jpg" alt="(!LANG:Untitled3.jpg" width="56" height="51">!}

Problémy lineárnej algebry. Pojem matice. Typy matríc. Operácie s maticami. Riešenie úloh o transformácii matíc.

Pri riešení rôznych matematických úloh sa často musíme zaoberať tabuľkami čísel nazývanými matice. Pomocou matíc je vhodné riešiť sústavy lineárnych rovníc, vykonávať mnohé operácie s vektormi, riešiť rôzne problémy počítačovej grafiky a iné inžinierske úlohy.

Matica sa nazýva obdĺžniková tabuľka čísel obsahujúca číslo m linky a niektoré P stĺpci. čísla t a P sa nazývajú maticové objednávky. Ak t = P, matica sa nazýva štvorec a číslo m = n- jej príkaz.

V nasledujúcom texte sa na zápis matíc použijú buď dvojité pomlčky alebo zátvorky:

Alebo

Pre krátke maticové označenie sa často použije buď jedno veľké latinské písmeno (napríklad A) alebo symbol || a ij || a niekedy s vysvetlenim: ALE = || a ij || = (aij), kde (i = 1, 2, ..., m, j = 1, 2, ..., n).

čísla aij, ktoré sú súčasťou tejto matice sa nazývajú jej prvky. Pri nahrávaní aij prvý index і znamená číslo riadku a druhý index j- číslo stĺpca. V prípade štvorcovej matice

(1.1)

zavádzajú sa pojmy hlavná a vedľajšia uhlopriečka. Hlavná uhlopriečka matice (1.1) je uhlopriečka od 11 do 12 … ann z ľavého horného rohu tejto matice do jej pravého dolného rohu. Bočná uhlopriečka tej istej matice sa nazýva uhlopriečka a n 1 a (n -1) 2… a 1 n , prechádza z ľavého dolného rohu do pravého horného rohu.

Základné operácie s maticami a ich vlastnosti.

Prejdime k definícii základných operácií s maticami.

Pridanie matice. Súčet dvoch matíc A = || a ij || , kde a B = || b ij || , kde (i = 1, 2, ..., m, j = 1, 2, ..., n) rovnaké príkazy t a P sa nazýva matica C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., n) rovnaké príkazy t a P, prvkov s ij ktoré sú určené vzorcom

, kde (i = 1, 2, ..., m, j = 1, 2, ..., n)(1.2)

Na označenie súčtu dvoch matíc používame zápis C \u003d A + B. Operácia skladania súčtu matíc sa nazýva ich sčítanie. Takže podľa definície:

+ =

Z definície súčtu matíc, respektíve zo vzorcov (1.2) priamo vyplýva, že operácia sčítania matíc má rovnaké vlastnosti ako operácia sčítania reálnych čísel, a to:

1) komutatívna vlastnosť: A + B = B + A,

2) kombinovaná vlastnosť: ( A + B) + C = A + (B + C).

Tieto vlastnosti umožňujú nedbať na poradie členov matíc pri pridávaní dvoch alebo viacerých matíc.

Násobenie matice číslom. Súčin matice A = || a ij || , kde (i = 1, 2, ..., m, j=1, 2, ..., n) reálnym číslom l, sa nazýva matica C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., n), ktorého prvky sú určené vzorcom:

, kde (i = 1, 2, ..., m, j = 1, 2, ..., n)(1.3)

Na označenie súčinu matice číslom sa používa zápis C \u003d l A alebo C \u003d A l. Operácia zostavenia súčinu matice číslom sa nazýva násobenie matice týmto číslom.

Zo vzorca (1.3) je zrejmé, že násobenie matice číslom má tieto vlastnosti:

1) asociatívna vlastnosť vzhľadom na číselný faktor: (l m) A = l (m A);

2) distribučná vlastnosť vzhľadom na súčet matíc: 1 (A + B) = 1 A + 1 B;

3) distributívna vlastnosť vzhľadom na súčet čísel: (l + m) A = lA + mA

Komentujte. Rozdiel dvoch matíc ALE a AT rovnaké objednávky t a P je prirodzené nazývať takú matricu S rovnaké príkazy t a P,čo celkovo s maticou B dáva maticu A. Prirodzený zápis sa používa na označenie rozdielu dvoch matíc: C \u003d A - B.

Je veľmi ľahké overiť tento rozdiel S dve matrice ALE a AT možno získať podľa pravidla C \u003d A + (-1) B.

Súčin matríc alebo násobenie matice.

Matrixový produkt A = || a ij || , kde (i = 1, 2, ..., m, j = 1, 2, ..., n) majúce objednávky, resp t a n, do matice B = || b ij || , kde (i = 1, 2, ..., n, j = 1, 2, ..., p), majúce objednávky rovnaké n a R, nazývaná matica C = || c ij || (i = 1,2, ..., m; j = 1, 2, ...., p), ktorý má objednávky, respektíve rovné t a R ktorých prvky sú určené vzorcom:

kde (i = 1, 2, ..., m, j = 1, 2, ..., p)(1.4)

Na označenie súčinu matice ALE do matice AT použiť záznam C = A × B. Operácia maticového produktu ALE do matice AT sa nazýva násobenie týchto matíc.

Z vyššie uvedenej definície vyplýva, že maticu A nemožno vynásobiť žiadnou maticou B, je potrebné, aby počet stĺpcov matice ALE sa rovnalo počtu riadkov matice AT.

Vzorec (1.4) je pravidlom na zostavenie prvkov matice C, ktorá je súčinom matice ALE do matice AT. Toto pravidlo možno formulovať aj slovne: prvok c i j nachádzajúci sa v priesečníku i-teho riadku a j-tého stĺpca matice C = A B sa rovná súčtu párových súčinov zodpovedajúcich prvkov i-teho riadku matice A a j-tý stĺpec matice B.

Ako príklad aplikácie tohto pravidla uvádzame vzorec na násobenie štvorcových matíc druhého rádu.

× =

Vzorec (1.4) naznačuje nasledujúce vlastnosti matricového produktu ALE na matricu AT:

1) asociatívna vlastnosť: (AB) C = A (BC);

2) distributívna vlastnosť vzhľadom na súčet matíc:

(A + B) C = AC + B C alebo A (B + C) = A B + AC.

Otázka permutačnej (komutatívnej) vlastnosti súčinu matice A do matice AT má zmysel nastavovať len pre štvorcové matice A a B rovnaké poradie.

Uvádzame dôležité špeciálne prípady matíc, pre ktoré platí aj permutačná vlastnosť. Dve matice, pre súčin ktorých platí permutačná vlastnosť, sa zvyčajne nazývajú komutovanie.

Medzi štvorcovými maticami vyčleňujeme triedu takzvaných diagonálnych matíc, z ktorých každá má prvky umiestnené mimo hlavnej uhlopriečky rovné nule. Každá diagonálna matica poriadku P má formu

D= (1.5)

kde d1, d2,… ,dn- ľubovoľné číslo. Je ľahké vidieť, že ak sú všetky tieto čísla navzájom rovnaké, t.j. d1=d2=… = d n potom pre ľubovoľnú štvorcovú maticu ALE objednať P spravodlivá rovnosť A D = D A.

Medzi všetkými diagonálnymi maticami (1.5) so zhodnými položkami d1=d2=… = d n = = d dve matrice zohrávajú obzvlášť dôležitú úlohu. Prvá z týchto matíc sa získa pomocou d = 1 sa nazýva matica identity n E. Druhá matica sa získa pomocou d=0, sa nazýva nulová matica n rádu a je označený symbolom Oh teda

E= O=

Na základe toho, čo bolo dokázané vyššie A E = E A a A O = O A. Navyše je ľahké to ukázať

A E \u003d E A \u003d A, A O \u003d O A \u003d 0. (1.6)

Prvý zo vzorcov (1.6) charakterizuje špeciálnu úlohu matice identity E, podobnú úlohu, ktorú zohráva číslo 1 pri násobení reálnych čísel. Čo sa týka špeciálnej úlohy nulovej matice ó, potom to prezrádza nielen druhý zo vzorcov (1.7), ale aj elementárne overiteľná rovnosť

A + 0 = 0 + A = A.

Na záver poznamenávame, že pojem nulová matica možno zaviesť aj pre neštvorcové matice (nula je tzv. akýkoľvek matice, ktorej všetky prvky sú rovné nule).

Blokové matice

Predpokladajme nejakú maticu A = || a ij || pomocou vodorovných a zvislých čiar sa rozdelí na samostatné pravouhlé bunky, z ktorých každá je maticou menších veľkostí a nazýva sa blok pôvodnej matice. V tomto prípade je možné zvážiť pôvodnú maticu ALE ako nejaká nová (tzv. bloková) matica ALE = || A a b ||, ktorého prvkami sú špecifikované bloky. Tieto prvky označujeme veľkým latinským písmenom, aby sme zdôraznili, že vo všeobecnosti ide o matice, nie čísla, a (ako bežné číselné prvky) dodávame dva indexy, z ktorých prvý označuje číslo riadku „bloku“ a druhý - číslo riadku „blok“. » stĺpec.

Napríklad matica

možno vidieť ako blokovú maticu

ktorých prvkami sú tieto bloky:

Pozoruhodný je fakt, že základné operácie s blokovými maticami sa vykonávajú podľa rovnakých pravidiel, podľa ktorých sa vykonávajú s bežnými číselnými maticami, len bloky fungujú ako prvky.

Pojem determinantu.

Uvažujme ľubovoľnú štvorcovú maticu ľubovoľného rádu P:

A= (1.7)

S každou takouto maticou spájame dobre definovanú číselnú charakteristiku, nazývanú determinant zodpovedajúci tejto matici.

Ak objednávka n matica (1.7) sa rovná jednej, potom táto matica pozostáva z jedného prvku a i j je determinant prvého rádu zodpovedajúci takejto matici, budeme nazývať hodnotu tohto prvku.

potom determinant druhého rádu zodpovedajúci takejto matici je číslo rovné od 11 do 22 - od 12 do 21 a označené jedným zo symbolov:

Takže podľa definície

(1.9)

Vzorec (1.9) je pravidlom na zostavenie determinantu druhého rádu z prvkov jemu zodpovedajúcej matice. Slovná formulácia tohto pravidla je nasledovná: determinant druhého rádu zodpovedajúci matici (1.8) sa rovná rozdielu medzi súčinom prvkov na hlavnej diagonále tejto matice a súčinom prvkov na jej vedľajšej diagonále. Determinanty druhého a vyššieho rádu sa široko používajú pri riešení sústav lineárnych rovníc.

Pozrime sa, ako to funguje operácie s maticami v systéme MathCad . Najjednoduchšie operácie maticovej algebry sú v MathCade implementované ako operátory. Písanie operátorov z hľadiska významu je čo najbližšie k ich matematickej činnosti. Každý operátor je vyjadrený zodpovedajúcim symbolom. Zvážte maticové a vektorové operácie MathCad 2001. Vektory sú špeciálnym prípadom matíc dimenzií n x 1, preto pre ne platia všetky rovnaké operácie ako pre matice, pokiaľ nie sú špecificky špecifikované obmedzenia (napríklad niektoré operácie sú použiteľné len pre štvorcové matice n x n). Niektoré akcie sú platné len pre vektory (napríklad skalárny súčin) a niektoré, napriek rovnakému pravopisu, pôsobia na vektory a matice odlišne.

q Po stlačení tlačidla OK sa otvorí pole pre zadávanie prvkov matice. Ak chcete zadať prvok matice, umiestnite kurzor na označené miesto a zadajte číslo alebo výraz z klávesnice.

Ak chcete vykonať akúkoľvek operáciu pomocou panela nástrojov, musíte:

q vyberte maticu a kliknite na tlačidlo operácie na paneli,

q alebo kliknite na tlačidlo v paneli a na označenú pozíciu zadajte názov matice.

Ponuka „Symboly“ obsahuje tri operácie - transponovať, invertovať, determinant.

To znamená, že napríklad môžete vypočítať determinant matice vykonaním príkazu Symboly/matice/determinant.

Číslo prvého riadku (a prvého stĺpca) matice MathCAD je uložené v premennej ORIGIN. Štandardne je odpočítavanie od nuly. V matematickom zápise je bežnejšie počítať od 1. Aby MathCAD rátal čísla riadkov a stĺpcov od 1, musíte nastaviť premennú ORIGIN:=1.

Funkcie určené na prácu s problémami lineárnej algebry sú zhromaždené v časti „Vektory a matice“ dialógového okna „Vložiť funkciu“ (pripomíname, že sa volá tlačidlom na paneli „Štandard“). Hlavné z týchto funkcií budú popísané neskôr.

Transpozícia

Podobné informácie.