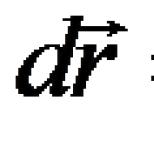Lineárna závislosť. Základ systému vektorov. Lineárna závislosť a lineárna nezávislosť vektorov. Základy vektorov. Afinný súradnicový systém Daný konečný systém vektorov nájsť

V článku o n -rozmerných vektoroch sme sa dostali ku konceptu lineárneho priestoru generovaného množinou n -rozmerných vektorov. Teraz musíme zvážiť nemenej dôležité pojmy, ako je rozmer a základ vektorového priestoru. Priamo súvisia s konceptom lineárne nezávislého systému vektorov, preto sa dodatočne odporúča pripomenúť si aj základy tejto témy.

Uveďme niekoľko definícií.

Definícia 1

Rozmer vektorového priestoru je číslo zodpovedajúce maximálnemu počtu lineárne nezávislých vektorov v tomto priestore.

Definícia 2

Vektorový priestorový základ- množina lineárne nezávislých vektorov, usporiadaných a počtom rovných rozmeru priestoru.

Uvažujme o určitom priestore n -vektorov. Jeho rozmer sa rovná n . Zoberme si systém n-jednotkových vektorov:

e (1) = (1, 0, ..., 0) e (2) = (0, 1, ..., 0) e (n) = (0, 0, ..., 1)

Použime tieto vektory ako zložky matice A: bude jednotkou s rozmerom n x n . Hodnosť tejto matice je n. Preto vektorový systém e (1) , e (2) , . . . , e (n) je lineárne nezávislé. V tomto prípade nie je možné pridať do systému jeden vektor bez narušenia jeho lineárnej nezávislosti.

Keďže počet vektorov v systéme je rovný n, potom sa rozmer priestoru n-rozmerných vektorov rovná n a jednotkové vektory e (1) , e (2) , . . . , e (n) sú základom určeného priestoru.

Zo získanej definície vyvodíme záver: akýkoľvek systém n-rozmerných vektorov, v ktorom je počet vektorov menší ako n, nie je základom priestoru.

Ak prehodíme prvý a druhý vektor, dostaneme sústavu vektorov e (2) , e (1) , . . . , e (n) . Bude tiež základom n-rozmerného vektorového priestoru. Zostavme maticu, pričom vektory výsledného systému budú mať ako jej riadky. Maticu možno získať z matice identity prehodením prvých dvoch riadkov, jej poradie sa bude rovnať n . Systém e (2) , e (1) , . . . , e (n) je lineárne nezávislý a je základom n-rozmerného vektorového priestoru.

Preusporiadaním iných vektorov v pôvodnom systéme získame ešte jeden základ.

Môžeme vziať lineárne nezávislý systém nejednotkových vektorov, čo bude tiež predstavovať základ n-rozmerného vektorového priestoru.

Definícia 3

Vektorový priestor s rozmerom n má toľko báz, koľko je lineárne nezávislých systémov n-rozmerných vektorov s číslom n.

Rovina je dvojrozmerný priestor - jeho základom budú dva ľubovoľné nekolineárne vektory. Akékoľvek tri nekoplanárne vektory budú slúžiť ako základ trojrozmerného priestoru.

Zvážte aplikáciu tejto teórie na konkrétnych príkladoch.

Príklad 1

Počiatočné údaje: vektory

a = (3 , - 2 , 1) b = (2 , 1 , 2) c = (3 , - 1 , - 2)

Je potrebné určiť, či špecifikované vektory sú základom trojrozmerného vektorového priestoru.

rozhodnutie

Na vyriešenie problému študujeme daný systém vektorov pre lineárnu závislosť. Urobme maticu, kde riadky sú súradnice vektorov. Určme poradie matice.

A = 3 2 3 - 2 1 - 1 1 2 - 2 A = 3 - 2 1 2 1 2 3 - 1 - 2 = 3 1 (- 2) + (- 2) 2 3 + 1 2 (- 1) - 1 1 3 - (- 2) 2 (- 2) - 3 2 (- 1) = = - 25 ≠ 0 ⇒ Ra n k (A) = 3

V dôsledku toho sú vektory dané podmienkou úlohy lineárne nezávislé a ich počet sa rovná rozmeru vektorového priestoru - sú základom vektorového priestoru.

odpoveď: tieto vektory sú základom vektorového priestoru.

Príklad 2

Počiatočné údaje: vektory

a = (3 , - 2 , 1) b = (2 , 1 , 2) c = (3 , - 1 , - 2) d = (0 , 1 , 2)

Je potrebné určiť, či uvedený systém vektorov môže byť základom trojrozmerného priestoru.

rozhodnutie

Systém vektorov zadaný v podmienke úlohy je lineárne závislý, od r maximálny počet lineárne nezávislých vektorov je 3. Tento systém vektorov teda nemôže slúžiť ako základ pre trojrozmerný vektorový priestor. Za zmienku však stojí, že podsystém pôvodného systému a = (3 , - 2 , 1) , b = (2 , 1 , 2) , c = (3 , - 1 , - 2) je základ.

odpoveď: uvedený systém vektorov nie je základom.

Príklad 3

Počiatočné údaje: vektory

a = (1, 2, 3, 3) ​​b = (2, 5, 6, 8) c = (1, 3, 2, 4) d = (2, 5, 4, 7)

Môžu byť základom štvorrozmerného priestoru?

rozhodnutie

Zostavte maticu pomocou súradníc daných vektorov ako riadkov

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

Pomocou Gaussovej metódy určíme poradie matice:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7 ~ 1 2 3 3 0 1 0 2 0 1 - 1 1 0 1 - 2 1 ~ ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 - 2 - 1 ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 0 1 ⇒ ⇒ R a n k (A) = 4

Preto je sústava daných vektorov lineárne nezávislá a ich počet sa rovná rozmeru vektorového priestoru – sú základom štvorrozmerného vektorového priestoru.

odpoveď: dané vektory sú základom štvorrozmerného priestoru.

Príklad 4

Počiatočné údaje: vektory

a (1) = (1 , 2 , - 1 , - 2) a (2) = (0 , 2 , 1 , - 3) a (3) = (1 , 0 , 0 , 5)

Tvoria základ 4-rozmerného priestoru?

rozhodnutie

Pôvodný systém vektorov je lineárne nezávislý, ale počet vektorov v ňom je nedostatočný na to, aby sa stal základom štvorrozmerného priestoru.

odpoveď: nie, nemajú.

Rozklad vektora z hľadiska bázy

Akceptujeme, že ľubovoľné vektory e (1) , e (2) , . . . , e (n) sú základom vektorového n-rozmerného priestoru. Pridajme k nim nejaký n-rozmerný vektor x →: výsledný systém vektorov sa stane lineárne závislým. Vlastnosti lineárnej závislosti uvádzajú, že aspoň jeden z vektorov takéhoto systému môže byť lineárne vyjadrený v podmienkach ostatných. Preformulovaním tohto tvrdenia môžeme povedať, že aspoň jeden z vektorov lineárne závislého systému môže byť rozšírený v iných vektoroch.

Tak sme sa dostali k formulácii najdôležitejšej vety:

Definícia 4

Akýkoľvek vektor n-rozmerného vektorového priestoru je jedinečne rozložený z hľadiska bázy.

Dôkaz 1

Dokážme túto vetu:

nastavte základ n-rozmerného vektorového priestoru - e (1) , e (2) , . . . , e (n) . Urobme systém lineárne závislým tak, že k nemu pridáme n-rozmerný vektor x →. Tento vektor môže byť lineárne vyjadrený v podmienkach pôvodných vektorov e:

x = x 1 e (1) + x 2 e (2) +. . . + x n e (n), kde x 1, x 2,. . . , x n - niektoré čísla.

Teraz dokážeme, že takýto rozklad je jedinečný. Predpokladajme, že to tak nie je a že existuje ďalšie podobné rozšírenie:

x = x ~ 1 e (1) + x 2 ~ e (2) +. . . + x ~ n e (n), kde x ~ 1, x ~ 2, . . . , x ~ n - niektoré čísla.

Odpočítajte od ľavej a pravej časti tejto rovnosti ľavú a pravú časť rovnosti x = x 1 · e (1) + x 2 · e (2) + . . . + x n e (n) . Dostaneme:

0 = (x ~ 1 - x 1) e (1) + (x ~ 2 - x 2) e (2) +. . . (x~n - xn) e(2)

Systém bázových vektorov e (1) , e (2) , . . . e (n) je lineárne nezávislé; Podľa definície lineárnej nezávislosti systému vektorov je vyššie uvedená rovnosť možná len vtedy, keď sú všetky koeficienty (x ~ 1 - x 1), (x ~ 2 - x 2), . . . , (x ~ n - x n) sa bude rovnať nule. Z čoho to bude spravodlivé: x 1 \u003d x ~ 1, x 2 \u003d x ~ 2,. . . , x n = x ~ n . A to je jediný spôsob, ako rozšíriť vektor z hľadiska základu.

V tomto prípade sú koeficienty x 1 , x 2 , . . . , x n sa nazývajú súradnice vektora x → v základe e (1) , e (2) , . . . , e (n) .

Overená teória objasňuje výraz „je daný n-rozmerný vektor x = (x 1 , x 2 ,..., x n)“: uvažuje sa vektor x → n-rozmerný vektorový priestor a jeho súradnice sú uvedené v nejaký základ. Je tiež jasné, že ten istý vektor v inej báze n-rozmerného priestoru bude mať rôzne súradnice.

Uvažujme o nasledujúcom príklade: predpokladajme, že v nejakej báze n-rozmerného vektorového priestoru je daný systém n lineárne nezávislých vektorov

a tiež je daný vektor x = (x 1, x 2,..., x n).

Vektory e 1 (1), e 2 (2), . . . , e n (n) sú v tomto prípade tiež základom tohto vektorového priestoru.

Predpokladajme, že je potrebné určiť súradnice vektora x → v základe e 1 (1) , e 2 (2) , . . . , e n (n) , označené ako x ~ 1 , x ~ 2 , . . . , x ~ n .

Vektor x → bude reprezentovaný takto:

x = x ~ 1 e (1) + x ~ 2 e (2) +. . . + x ~ n e (n)

Tento výraz napíšeme v súradnicovom tvare:

(x 1 , x 2 , ..., x n) = x ~ 1 (e (1) 1, e (1) 2, ..., e (1) n) + x ~ 2 (e (2) 1 , e (2) 2, ..., e (2) n) +. . . + + x ~ n (e (n) 1, e (n) 2,..., e (n) n) = = (x ~ 1 e 1 (1) + x ~ 2 e 1 (2) +. ... + x ~ n e 1 (n), x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + + ... + x ~ n e 2 (n) , ... , x ~ 1 e n (1) + x ~ 2 n (2) + ... + x ~ n n (n))

Výsledná rovnosť je ekvivalentná systému n lineárnych algebraických výrazov s n neznámymi lineárnymi premennými x ~ 1 , x ~ 2 , . . . , x ~ n:

x 1 = x ~ 1 e 1 1 + x ~ 2 e 1 2 + . . . + x ~ n e 1 n x 2 = x ~ 1 e 2 1 + x ~ 2 e 2 2 +. . . + x ~ n e 2 n ⋮ x n = x ~ 1 e n 1 + x ~ 2 e n 2 +. . . + x ~ n e n n

Matica tohto systému bude vyzerať takto:

e 1 (1) e 1 (2) ⋯ e 1 (n) e 2 (1) e 2 (2) ⋯ e 2 (n) ⋮ ⋮ ⋮ ⋮ e n (1) e n (2) ⋯ e n (n)

Nech je to matica A a jej stĺpce sú vektory lineárne nezávislého systému vektorov e 1 (1) , e 2 (2) , . . . , en (n) . Hodnosť matice je n a jej determinant je nenulový. To naznačuje, že systém rovníc má jedinečné riešenie, ktoré možno určiť akýmkoľvek vhodným spôsobom: napríklad Cramerovou metódou alebo maticovou metódou. Takto vieme určiť súradnice x ~ 1 , x ~ 2 , . . . , x ~ n vektora x → v základe e 1 (1) , e 2 (2) , . . . , en (n) .

Aplikujme uvažovanú teóriu na konkrétnom príklade.

Príklad 6

Počiatočné údaje: vektory sú dané na báze trojrozmerného priestoru

e (1) = (1 , - 1 , 1) e (2) = (3 , 2 , - 5) e (3) = (2 , 1 , - 3) x = (6 , 2 , - 7)

Je potrebné potvrdiť skutočnosť, že ako základ daného priestoru slúži aj sústava vektorov e (1) , e (2) , e (3) a tiež určiť súradnice vektora x v danej báze. .

rozhodnutie

Systém vektorov e (1) , e (2) , e (3) bude základom trojrozmerného priestoru, ak bude lineárne nezávislý. Túto možnosť zistíme určením hodnosti matice A , ktorej riadky sú dané vektory e (1) , e (2) , e (3) .

Používame Gaussovu metódu:

A = 1 - 1 1 3 2 - 5 2 1 - 3 ~ 1 - 1 1 0 5 - 8 0 3 - 5 ~ 1 - 1 1 0 5 - 8 0 0 - 1 5

Rank (A) = 3. Systém vektorov e (1) , e (2) , e (3) je teda lineárne nezávislý a je bázou.

Nech vektor x → v základe má súradnice x ~ 1 , x ~ 2 , x ~ 3 . Spojenie týchto súradníc je určené rovnicou:

x 1 = x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + x ~ 3 e 1 (3) x 2 = x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + x ~ 3 e 2 (3) x 3 = x ~ 1 e 3 (1) + x ~ 2 e 3 (2) + x ~ 3 e 3 (3)

Aplikujme hodnoty podľa podmienok problému:

x ~ 1 + 3 x ~ 2 + 2 x ~ 3 = 6 - x ~ 1 + 2 x ~ 2 + x ~ 3 = 2 x ~ 1 - 5 x ~ 2 - 3 x 3 = - 7

Sústavu rovníc riešime Cramerovou metódou:

∆ = 1 3 2 - 1 2 1 1 - 5 - 3 = - 1 ∆ x ~ 1 = 6 3 2 2 2 1 - 7 - 5 - 3 = - 1 , x ~ 1 = ∆ x ~ 1 ∆ = - 1 - 1 = 1 ∆ x ~ 2 = 1 6 2 - 1 2 1 1 - 7 - 3 = - 1 , x ~ 2 = ∆ x ~ 2 ∆ = - 1 - 1 = 1 ∆ x ~ 3 = 1 3 6 - 1 2 2 1 - 5 - 7 = - 1 , x ~ 3 = ∆ x ~ 3 ∆ = - 1 - 1 = 1

Takže vektor x → v základe e (1) , e (2) , e (3) má súradnice x ~ 1 = 1 , x ~ 2 = 1 , x ~ 3 = 1 .

odpoveď: x = (1, 1, 1)

Spojenie medzi základňami

Predpokladajme, že v nejakom základe n-rozmerného vektorového priestoru sú dané dva lineárne nezávislé systémy vektorov:

c (1) = (c 1 (1) , c 2 (1) ,..., cn (1)) c (2) = (c 1 (2), c 2 (2) ,..., cn (2)) ⋮ c (n) = (c 1 (n) , e 2 (n) ,..., c n (n))

e (1) = (e 1 (1) , e 2 (1), ..., e n (1)) e (2) = (e 1 (2), e 2 (2), ..., e n (2)) ⋮ e (n) = (e 1 (n) , e 2 (n) ,..., e n (n))

Tieto systémy sú zároveň základmi daného priestoru.

Nech c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1) - súradnice vektora c (1) v báze e (1) , e (2) , . . . , e (3) , potom vzťah súradníc bude daný sústavou lineárnych rovníc:

c 1 (1) = c ~ 1 (1) e 1 (1) + c ~ 2 (1) e 1 (2) +. . . + c ~ n (1) e 1 (n) c 2 (1) = c ~ 1 (1) e 2 (1) + c ~ 2 (1) e 2 (2) +. . . + c ~ n (1) e 2 (n) ⋮ c n (1) = c ~ 1 (1) e n (1) + c ~ 2 (1) e n (2) + . . . + c ~ n (1) a n (n)

Vo forme matice môže byť systém zobrazený nasledovne:

(c 1 (1), c 2 (1),..., c n (1)) = (c ~ 1 (1), c ~ 2 (1) , .. ., c ~ n (1)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ 1 (n) e 2 (n) … e n (n)

Urobme rovnaký zápis pre vektor c (2) analogicky:

(c 1 (2), c 2 (2) ,..., c n (2)) = (c ~ 1 (2) , c ~ 2 (2) , .. ., c ~ n (2)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ 1 (n) e 2 (n) … e n (n)

(c 1 (n), c 2 (n) , ..., c n (n)) = (c ~ 1 (n) , c ~ 2 (n) , .. ., c ~ n (n)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ 1 (n) e 2 (n) … e n (n)

Maticové rovnosti sú spojené do jedného výrazu:

c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n) = c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n ) e 2 (n) ⋯ e n (n)

Určí vzťah vektorov dvoch rôznych báz.

Rovnakým princípom je možné vyjadriť všetky bázové vektory e (1) , e (2) , . . . , e (3) cez základ c (1) , c (2) , . . . , c (n):

e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n) = e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n ) c 2 (n) ⋯ c n (n)

Uvádzame nasledujúce definície:

Definícia 5

Matica c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) je matica prechodu zo základu e (1) , e (2) , . . . , e(3)

na základ c (1) , c (2) , . . . , c (n) .

Definícia 6

Matica e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) je matica prechodu zo základu c (1) , c (2) , . . . ,c(n)

na základ e (1) , e (2) , . . . e (3).

Z týchto rovností je zrejmé, že

c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 e ~ 1 (1) e ~ 1 (1) e ) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n ) c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1

tie. prechodové matice sú vzájomne inverzné.

Zoberme si teóriu na konkrétnom príklade.

Príklad 7

Počiatočné údaje: je potrebné nájsť maticu prechodu zo základu

c (1) = (1, 2, 1) c (2) = (2, 3, 3) ​​c (3) = (3, 7, 1)

e (1) = (3, 1, 4) e (2) = (5, 2, 1) e (3) = (1, 1, - 6)

Tiež je potrebné špecifikovať vzťah súradníc ľubovoľného vektora x → v daných bázach.

rozhodnutie

1. Nech T je matica prechodu, potom bude rovnosť pravdivá:

3 1 4 5 2 1 1 1 1 = T 1 2 1 2 3 3 3 7 1

Vynásobte obe strany rovnice

1 2 1 2 3 3 3 7 1 - 1

a získaj:

T = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1

2. Definujte prechodovú maticu:

T = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1 = = 3 1 4 5 2 1 1 1 - 6 - 18 5 3 7 - 2 - 1 5 - 1 - 1 = - 27 9 4 - 71 20 12 - 41 9 8

3. Definujte vzťah súradníc vektora x → :

predpokladajme, že v základe c (1) , c (2) , . . . , c (n) vektor x → má súradnice x 1 , x 2 , x 3 , potom:

x \u003d (x 1, x 2, x 3) 1 2 1 2 3 3 3 7 1,

a v základe e (1) , e (2) , . . . , e (3) má súradnice x ~ 1 , x ~ 2 , x ~ 3 , potom:

x = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 - 6

Pretože ľavé časti týchto rovníc sú rovnaké, môžeme rovnať aj pravé časti:

(x 1 , x 2 , x 3) 1 2 1 2 3 3 3 7 1 = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 - 6

Vynásobte obe strany vpravo

1 2 1 2 3 3 3 7 1 - 1

a získaj:

(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1 ⇔ ⇔ ( x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) T ⇔ ⇔ (x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3 ) - 27 9 4 – 71 20 12 – 41 9 8

Na druhej strane

(x ~ 1, x ~ 2, x ~ 3) = (x 1, x 2, x 3) - 27 9 4 - 71 20 12 - 41 9 8

Posledné rovnosti ukazujú vzťah súradníc vektora x → v oboch bázach.

odpoveď: prechodová matica

27 9 4 - 71 20 12 - 41 9 8

Súradnice vektora x → v daných bázach súvisia vzťahom:

(x 1, x 2, x 3) = (x ~ 1, x ~ 2, x ~ 3) - 27 9 4 - 71 20 12 - 41 9 8

(x ~ 1, x ~ 2, x ~ 3) = (x 1, x 2, x 3) - 27 9 4 - 71 20 12 - 41 9 8 - 1

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Lineárna závislosť a lineárna nezávislosť vektorov.
Základy vektorov. Afinný súradnicový systém

V hľadisku je vozík s čokoládami a dnes každý návštevník dostane sladkú dvojicu - analytickú geometriu s lineárnou algebrou. Tento článok sa dotkne dvoch častí vyššej matematiky naraz a uvidíme, ako spolu vychádzajú v jednom obale. Dajte si pauzu, zjedzte Twix! ... sakra, no, argumentovať nezmysly. Aj keď v poriadku, nedám gól, nakoniec by mal existovať pozitívny prístup k štúdiu.

Lineárna závislosť vektorov, lineárna nezávislosť vektorov, vektorový základ a iné pojmy majú nielen geometrický výklad, ale predovšetkým algebraický význam. Samotný pojem „vektor“ z pohľadu lineárnej algebry zďaleka nie je vždy tým „obyčajným“ vektorom, ktorý môžeme zobraziť v rovine alebo v priestore. Dôkaz nemusíte hľadať ďaleko, skúste nakresliť vektor päťrozmerného priestoru . Alebo vektor počasia, pre ktorý som si šiel práve do Gismetea: - teplota a atmosférický tlak, resp. Príklad je, samozrejme, nesprávny z hľadiska vlastností vektorového priestoru, ale napriek tomu nikto nezakazuje formalizovať tieto parametre ako vektor. Dych jesene...

Nie, nebudem vás nudiť teóriou, lineárne vektorové priestory, úlohou je rozumieť definície a vety. Nové pojmy (lineárna závislosť, nezávislosť, lineárna kombinácia, báza atď.) sú z algebraického hľadiska použiteľné pre všetky vektory, ale príklady budú uvedené geometricky. Všetko je teda jednoduché, prístupné a vizuálne. Okrem problémov analytickej geometrie sa budeme zaoberať aj niektorými typickými úlohami algebry. Na zvládnutie materiálu je vhodné oboznámiť sa s lekciami Vektory pre figuríny a Ako vypočítať determinant?

Lineárna závislosť a nezávislosť rovinných vektorov.
Rovinný základ a afinný súradnicový systém

Zvážte rovinu vášho počítačového stola (stačí stôl, nočný stolík, podlaha, strop, čokoľvek sa vám páči). Úloha bude pozostávať z nasledujúcich akcií:

1) Vyberte základ roviny. Zhruba povedané, doska stola má dĺžku a šírku, takže je intuitívne jasné, že na zostavenie základu sú potrebné dva vektory. Jeden vektor zjavne nestačí, tri vektory sú príliš veľa.

2) Na základe zvoleného základu nastaviť súradnicový systém(súradnicová mriežka) na priradenie súradníc všetkým položkám v tabuľke.

Nebuďte prekvapení, najprv budú vysvetlenia na prstoch. Navyše na tej vašej. Umiestnite prosím ukazovák ľavej ruky na okraj dosky stola tak, aby sa pozeral na monitor. Toto bude vektor. Teraz miesto malíček pravej ruky na okraj stola rovnakým spôsobom - tak, aby smeroval na obrazovku monitora. Toto bude vektor. Usmej sa, vyzeráš skvele! Čo možno povedať o vektoroch? Dátové vektory kolineárne, čo znamená lineárne vyjadrené cez seba:
, no, alebo naopak: , kde je nenulové číslo.

Obrázok tejto akcie môžete vidieť v lekcii. Vektory pre figuríny, kde som vysvetlil pravidlo pre násobenie vektora číslom.

Nastavia vaše prsty základ v rovine počítačového stola? Očividne nie. Kolineárne vektory sa pohybujú tam a späť sám smer, zatiaľ čo rovina má dĺžku a šírku.

Takéto vektory sa nazývajú lineárne závislé.

Referencia: Slová "lineárny", "lineárny" označujú skutočnosť, že v matematických rovniciach, výrazoch neexistujú žiadne mocniny, mocniny, logaritmy, sínusy atď. Existujú iba lineárne (1. stupeň) výrazy a závislosti.

Dva rovinné vektory lineárne závislé vtedy a len vtedy, ak sú kolineárne.

Prekrížte prsty na stole tak, aby medzi nimi bol akýkoľvek uhol okrem 0 alebo 180 stupňov. Dva rovinné vektorylineárne nie sú závislé vtedy a len vtedy, ak nie sú kolineárne. Takže základ je prijatý. Netreba sa hanbiť, že základ sa ukázal ako „šikmý“ s nekolmými vektormi rôznych dĺžok. Veľmi skoro uvidíme, že na jeho konštrukciu je vhodný nielen uhol 90 stupňov, ale nielen jednotkové vektory rovnakej dĺžky.

akýkoľvek rovinný vektor jediná cesta rozšírené z hľadiska základu:
, kde sú reálne čísla . Volajú sa čísla vektorové súradnice v tomto základe.

Aj to hovoria vektorprezentované vo formulári lineárna kombinácia bázové vektory. To znamená, že výraz sa nazýva vektorový rozkladzáklad alebo lineárna kombinácia bázové vektory.

Napríklad možno povedať, že vektor je expandovaný v ortonormálnom základe roviny , alebo možno povedať, že je reprezentovaný ako lineárna kombinácia vektorov .

Poďme formulovať definícia základu formálne: rovinný základ je dvojica lineárne nezávislých (nekolineárnych) vektorov, , kde akýkoľvek rovinný vektor je lineárnou kombináciou základných vektorov.

Podstatným bodom definície je fakt, že sa berú vektory v určitom poradí. základne Toto sú dva úplne odlišné základy! Ako sa hovorí, malíček ľavej ruky sa nedá presunúť na miesto malíčka pravej ruky.

Základ sme vymysleli, no nestačí nastaviť súradnicovú mriežku a priradiť súradnice každej položke na vašom počítači. Prečo nie dosť? Vektory sú voľné a putujú po celej rovine. Ako teda priradíte súradnice k tým malým špinavým bodkám tabuľky, ktoré zostali z divokého víkendu? Je potrebný východiskový bod. A takýmto referenčným bodom je bod známy každému - počiatok súradníc. Pochopenie súradnicového systému:

Začnem „školským“ systémom. Už v úvodnej lekcii Vektory pre figuríny Zdôraznil som niektoré rozdiely medzi pravouhlým súradnicovým systémom a ortonormálnym základom. Tu je štandardný obrázok:

Keď sa hovorí o pravouhlý súradnicový systém, potom najčastejšie znamenajú počiatok, súradnicové osi a mierku pozdĺž osí. Skúste zadať do vyhľadávača „obdĺžnikový súradnicový systém“ a uvidíte, že mnohé zdroje vám prezradia, aké súradnicové osi sú známe z 5. – 6. ročníka a ako zakresľovať body do roviny.

Na druhej strane vzniká dojem, že pravouhlý súradnicový systém možno dobre definovať z hľadiska ortonormálneho základu. A takmer je. Znenie znie takto:

pôvodu a ortonormálny základná sada Kartézsky súradnicový systém roviny . Teda pravouhlý súradnicový systém určite je definovaný jedným bodom a dvoma jednotkovými ortogonálnymi vektormi. Preto vidíte výkres, ktorý som uviedol vyššie - v geometrických úlohách sa často (ale zďaleka nie vždy) kreslia vektory aj súradnicové osi.

Myslím, že to každý pochopí pomocou bodu (pôvodu) a ortonormálneho základu AKÝKOĽVEK BOD roviny a AKÝKOĽVEK VEKTOR roviny je možné priradiť súradnice. Obrazne povedané, „všetko v lietadle sa dá očíslovať“.

Musia byť súradnicové vektory jednotkové? Nie, môžu mať ľubovoľnú nenulovú dĺžku. Uvažujme bod a dva ortogonálne vektory ľubovoľnej nenulovej dĺžky:

Takýto základ je tzv ortogonálne. Počiatok súradníc s vektormi definuje súradnicovú sieť a ľubovoľný bod roviny, ľubovoľný vektor má svoje súradnice v danej báze. Napríklad, alebo. Zjavnou nevýhodou je, že súradnicové vektory všeobecne majú rôzne dĺžky iné ako jednota. Ak sú dĺžky rovné jednej, získa sa obvyklý ortonormálny základ.

! Poznámka : v ortogonálnej základni, ako aj pod afinnými základňami roviny a priestoru sa berú do úvahy jednotky pozdĺž osí PODMIENKY. Napríklad jedna jednotka pozdĺž úsečky obsahuje 4 cm, jedna jednotka pozdĺž ordináty obsahuje 2 cm.Táto informácia je dostatočná na to, aby sme v prípade potreby previedli „neštandardné“ súradnice na „naše obvyklé centimetre“.

A druhá otázka, ktorá už bola vlastne zodpovedaná - je potrebné, aby uhol medzi základnými vektormi bol rovný 90 stupňom? nie! Ako hovorí definícia, základné vektory musia byť len nekolineárne. V súlade s tým môže byť uhol akýkoľvek okrem 0 a 180 stupňov.

Bod v lietadle tzv pôvodu a nekolineárne vektory, , sada afinný súradnicový systém roviny :

Niekedy sa tento súradnicový systém nazýva šikmé systém. Body a vektory sú na obrázku znázornené ako príklady:

Ako viete, afinný súradnicový systém je ešte menej pohodlný, vzorce pre dĺžky vektorov a segmentov, ktoré sme zvažovali v druhej časti lekcie, v ňom nefungujú. Vektory pre figuríny, veľa lahodných vzorcov súvisiacich s skalárny súčin vektorov. Ale platia pravidlá pre sčítanie vektorov a násobenie vektora číslom, vzorce na delenie segmentu v tomto ohľade, ako aj niektoré ďalšie typy problémov, ktoré čoskoro zvážime.

A záver je taký, že najvhodnejším konkrétnym prípadom afinného súradnicového systému je karteziánsky pravouhlý systém. Preto ju, jej vlastnú, treba najčastejšie vidieť. ... Všetko v tomto živote je však relatívne - je veľa situácií, v ktorých je vhodné mať šikmý (alebo nejaký iný napr. polárny) súradnicový systém. Áno, a humanoidom môžu takéto systémy prísť na chuť =)

Prejdime k praktickej časti. Všetky problémy v tejto lekcii platia pre pravouhlý súradnicový systém aj pre všeobecný afinný prípad. Nie je tu nič zložité, všetok materiál je dostupný aj pre školáka.

Ako určiť kolinearitu rovinných vektorov?

Typická vec. Aby boli dva rovinné vektory sú kolineárne, je potrebné a postačujúce, aby ich príslušné súradnice boli proporcionálne.V podstate ide o súradnicu po súradnici spresnenie zjavného vzťahu .

Príklad 1

a) Skontrolujte, či sú vektory kolineárne .
b) Tvoria vektory základ? ?

rozhodnutie:
a) Zistite, či existuje pre vektory koeficient proporcionality tak, aby boli splnené rovnosti:

Určite vám poviem o „foppish“ verzii aplikácie tohto pravidla, ktorá v praxi funguje celkom dobre. Cieľom je okamžite zostaviť pomer a zistiť, či je správny:

Urobme pomer z pomerov zodpovedajúcich súradníc vektorov:

Skracujeme:
, takže zodpovedajúce súradnice sú úmerné, preto

Je možné vytvoriť vzťah a naopak, toto je ekvivalentná možnosť:

Na samotestovanie sa dá využiť skutočnosť, že kolineárne vektory sú lineárne vyjadrené cez seba. V tomto prípade ide o rovnosť . Ich platnosť sa dá ľahko skontrolovať pomocou elementárnych operácií s vektormi:

b) Dva rovinné vektory tvoria základ, ak nie sú kolineárne (lineárne nezávislé). Skúmame kolinearitu vektorov . Vytvorme si systém:

Z prvej rovnice vyplýva, že , z druhej rovnice vyplýva, že , čo znamená, systém je nekonzistentný(žiadne riešenia). Zodpovedajúce súradnice vektorov teda nie sú proporcionálne.

Záver: vektory sú lineárne nezávislé a tvoria základ.

Zjednodušená verzia riešenia vyzerá takto:

Zostavte pomer zo zodpovedajúcich súradníc vektorov :
, preto sú tieto vektory lineárne nezávislé a tvoria základ.

Obyčajne recenzenti túto možnosť neodmietajú, no problém nastáva v prípadoch, keď sa niektoré súradnice rovnajú nule. Páči sa ti to: . Alebo takto: . Alebo takto: . Ako sa tu prepracovať k pomeru? (Naozaj sa nedá deliť nulou). Z tohto dôvodu som zjednodušené riešenie nazval „fupské“.

odpoveď: a) , b) formulár.

Malý kreatívny príklad pre nezávislé riešenie:

Príklad 2

Pri akej hodnote parametra vektory bude kolineárny?

Vo vzorovom roztoku sa parameter zistí prostredníctvom podielu.

Existuje elegantný algebraický spôsob, ako skontrolovať kolinearitu vektorov. Systematizujme naše znalosti a pridajte ich ako piaty bod:

Pre dva rovinné vektory sú nasledujúce tvrdenia ekvivalentné:

2) vektory tvoria základ;
3) vektory nie sú kolineárne;

+ 5) determinant zložený zo súradníc týchto vektorov je nenulový.

resp. nasledujúce opačné tvrdenia sú ekvivalentné:
1) vektory sú lineárne závislé;
2) vektory netvoria základ;
3) vektory sú kolineárne;
4) vektory môžu byť navzájom lineárne vyjadrené;
+ 5) determinant zložený zo súradníc týchto vektorov sa rovná nule.

Veľmi, veľmi dúfam, že v tejto chvíli už rozumiete všetkým pojmom a vyhláseniam, s ktorými ste sa stretli.

Pozrime sa bližšie na nový, piaty bod: dva rovinné vektory sú kolineárne práve vtedy, ak sa determinant zložený zo súradníc daných vektorov rovná nule:. Aby ste túto funkciu mohli používať, samozrejme, musíte byť schopní nájsť determinanty.

my sa rozhodneme Príklad 1 druhým spôsobom:

a) Vypočítajte determinant, zložený zo súradníc vektorov :
, takže tieto vektory sú kolineárne.

b) Dva rovinné vektory tvoria základ, ak nie sú kolineárne (lineárne nezávislé). Vypočítajme determinant zložený zo súradníc vektorov :
, preto sú vektory lineárne nezávislé a tvoria základ.

odpoveď: a) , b) formulár.

Vyzerá oveľa kompaktnejšie a krajšie ako riešenie s proporciami.

Pomocou uvažovaného materiálu je možné stanoviť nielen kolinearitu vektorov, ale aj dokázať rovnobežnosť segmentov, priamok. Zvážte niekoľko problémov so špecifickými geometrickými tvarmi.

Príklad 3

Zadané sú vrcholy štvoruholníka. Dokážte, že štvoruholník je rovnobežník.

Dôkaz: V úlohe nie je potrebné vytvárať kresbu, pretože riešenie bude čisto analytické. Pamätajte na definíciu rovnobežníka:
Paralelogram Nazýva sa štvoruholník, v ktorom sú protiľahlé strany párovo rovnobežné.

Preto je potrebné preukázať:
1) rovnobežnosť protiľahlých strán a;
2) rovnobežnosť protiľahlých strán a .

Dokazujeme:

1) Nájdite vektory:

2) Nájdite vektory:

Výsledkom je rovnaký vektor („podľa školy“ - rovnaké vektory). Kolinearita je celkom zrejmá, ale je lepšie sa rozhodnúť správne, s usporiadaním. Vypočítajte determinant zložený zo súradníc vektorov:
, takže tieto vektory sú kolineárne a .

Záver: Protiľahlé strany štvoruholníka sú po pároch rovnobežné, takže podľa definície ide o rovnobežník. Q.E.D.

Viac dobrých a odlišných postáv:

Príklad 4

Zadané sú vrcholy štvoruholníka. Dokážte, že štvoruholník je lichobežník.

Pre presnejšiu formuláciu dôkazu je samozrejme lepšie získať definíciu lichobežníka, ale stačí si len zapamätať, ako vyzerá.

Toto je úloha pre nezávislé rozhodnutie. Kompletné riešenie na konci lekcie.

A teraz je čas pomaly sa presunúť z lietadla do vesmíru:

Ako určiť kolinearitu priestorových vektorov?

Pravidlo je veľmi podobné. Aby boli dva priestorové vektory kolineárne, je potrebné a postačujúce, aby ich zodpovedajúce súradnice boli úmerné.

Príklad 5

Zistite, či sú nasledujúce priestorové vektory kolineárne:

a) ;
b)
v)

rozhodnutie:
a) Skontrolujte, či existuje koeficient úmernosti pre zodpovedajúce súradnice vektorov:

Systém nemá žiadne riešenie, čo znamená, že vektory nie sú kolineárne.

"Zjednodušené" sa robí kontrolou pomeru. V tomto prípade:
– zodpovedajúce súradnice nie sú proporcionálne, čo znamená, že vektory nie sú kolineárne.

odpoveď: vektory nie sú kolineárne.

b-c) Toto sú body pre nezávislé rozhodnutie. Vyskúšajte to dvoma spôsobmi.

Existuje metóda na kontrolu kolinearity priestorových vektorov a prostredníctvom determinantu tretieho rádu, táto metóda je uvedená v článku Krížový súčin vektorov.

Podobne ako v prípade roviny možno uvažované nástroje použiť na štúdium rovnobežnosti priestorových segmentov a čiar.

Vitajte v druhej časti:

Lineárna závislosť a nezávislosť trojrozmerných priestorových vektorov.
Priestorová báza a afinný súradnicový systém

Mnohé zo zákonitostí, ktoré sme zvažovali v lietadle, budú platiť aj pre vesmír. Snažil som sa minimalizovať zhrnutie teórie, keďže leví podiel informácií už bol prežutý. Napriek tomu vám odporúčam pozorne si prečítať úvodnú časť, keďže sa objavia nové pojmy a pojmy.

Teraz namiesto roviny počítačového stola preskúmajme trojrozmerný priestor. Najprv vytvoríme jeho základ. Niekto je teraz vnútri, niekto vonku, no v žiadnom prípade nemôžeme utiecť z troch rozmerov: šírky, dĺžky a výšky. Na vytvorenie základne sú preto potrebné tri priestorové vektory. Jeden alebo dva vektory nestačia, štvrtý je nadbytočný.

A opäť sa zahrejeme na prstoch. Zdvihnite ruku a roztiahnite ju rôznymi smermi palec, ukazovák a prostredník. Budú to vektory, vyzerajú rôznymi smermi, majú rôzne dĺžky a majú rôzne uhly medzi sebou. Gratulujeme, základ trojrozmerného priestoru je pripravený! Mimochodom, nemusíte to demonštrovať učiteľom, bez ohľadu na to, ako krútite prstami, ale nemôžete sa dostať preč od definícií =)

Ďalej si položíme dôležitú otázku, či nejaké tri vektory tvoria základ trojrozmerného priestoru? Pevne zatlačte tromi prstami na dosku stola počítača. Čo sa stalo? Tri vektory sú umiestnené v rovnakej rovine a zhruba povedané, stratili sme jedno z meraní - výšku. Takéto vektory sú koplanárny a je celkom zrejmé, že základ trojrozmerného priestoru nie je vytvorený.

Treba si uvedomiť, že koplanárne vektory nemusia ležať v rovnakej rovine, môžu byť v rovnobežných rovinách (len to nerobte prstami, len Salvador Dali sa tak vytratil =)).

Definícia: vektory sa nazývajú koplanárny ak existuje rovina, s ktorou sú rovnobežné. Tu je logické dodať, že ak takáto rovina neexistuje, potom vektory nebudú koplanárne.

Tri koplanárne vektory sú vždy lineárne závislé, to znamená, že sú lineárne vyjadrené cez seba. Pre jednoduchosť si opäť predstavte, že ležia v rovnakej rovine. Po prvé, vektory nie sú len koplanárne, ale môžu byť aj kolineárne, potom môže byť akýkoľvek vektor vyjadrený prostredníctvom akéhokoľvek vektora. V druhom prípade, ak napríklad vektory nie sú kolineárne, tretí vektor sa cez ne vyjadrí jedinečným spôsobom: (a prečo je ľahké uhádnuť z materiálov predchádzajúcej časti).

Opak je tiež pravdou: tri nekoplanárne vektory sú vždy lineárne nezávislé, to znamená, že nie sú žiadnym spôsobom vyjadrené cez seba. A samozrejme, iba takéto vektory môžu tvoriť základ trojrozmerného priestoru.

Definícia: Základ trojrozmerného priestoru sa nazýva trojica lineárne nezávislých (nekoplanárnych) vektorov, prijaté v určitom poradí, zatiaľ čo ľubovoľný vektor priestoru jediná cesta expanduje v danom základe , kde sú súradnice vektora v danom základe

Pre pripomenutie môžete tiež povedať, že vektor je reprezentovaný ako lineárna kombinácia bázové vektory.

Koncept súradnicového systému je zavedený presne rovnakým spôsobom ako v prípade roviny, postačuje jeden bod a akékoľvek tri lineárne nezávislé vektory:

pôvodu a nekoplanárne vektory, prijaté v určitom poradí, sada afinný súradnicový systém trojrozmerného priestoru :

Samozrejme, že súradnicová mriežka je „šikmá“ a nepohodlná, ale napriek tomu nám vytvorený súradnicový systém umožňuje určite určiť súradnice ľubovoľného vektora a súradnice ľubovoľného bodu v priestore. Podobne ako v rovine, v afinnom súradnicovom systéme priestoru nebudú fungovať niektoré vzorce, ktoré som už spomínal.

Najznámejší a najpohodlnejší špeciálny prípad afinného súradnicového systému, ako si každý môže domyslieť, je pravouhlý priestorový súradnicový systém:

bod v priestore tzv pôvodu a ortonormálny základná sada Kartézsky súradnicový systém priestoru . známy obrázok:

Predtým, ako pristúpime k praktickým úlohám, opäť systematizujeme informácie:

Pre tri priestorové vektory sú nasledujúce tvrdenia ekvivalentné:
1) vektory sú lineárne nezávislé;
2) vektory tvoria základ;
3) vektory nie sú koplanárne;
4) vektory nemôžu byť lineárne vyjadrené cez seba;
5) determinant zložený zo súradníc týchto vektorov je odlišný od nuly.

Opačné tvrdenia sú podľa mňa pochopiteľné.

Lineárna závislosť / nezávislosť priestorových vektorov sa tradične kontroluje pomocou determinantu (položka 5). Zostávajúce praktické úlohy budú mať vyslovene algebraický charakter. Je čas zavesiť geometrickú palicu na klinec a oháňať sa baseballovou pálkou z lineárnej algebry:

Tri priestorové vektory sú koplanárne vtedy a len vtedy, ak sa determinant zložený zo súradníc daných vektorov rovná nule: .

Upozorňujem na malú technickú nuanciu: súradnice vektorov je možné písať nielen do stĺpcov, ale aj do riadkov (hodnota determinantu sa od toho nezmení - pozri vlastnosti determinantov). Ale je to oveľa lepšie v stĺpcoch, pretože je to výhodnejšie na riešenie niektorých praktických problémov.

Pre tých čitateľov, ktorí trochu zabudli na metódy výpočtu determinantov, alebo sa možno vôbec zle orientujú, odporúčam jednu z mojich najstarších lekcií: Ako vypočítať determinant?

Príklad 6

Skontrolujte, či nasledujúce vektory tvoria základ trojrozmerného priestoru:

rozhodnutie: V skutočnosti celé riešenie spočíva vo výpočte determinantu.

a) Vypočítajte determinant zložený zo súradníc vektorov (determinant je rozšírený na prvom riadku):

, čo znamená, že vektory sú lineárne nezávislé (nie koplanárne) a tvoria základ trojrozmerného priestoru.

Odpoveď: tieto vektory tvoria základ

b) Toto je bod pre nezávislé rozhodnutie. Úplné riešenie a odpoveď na konci hodiny.

Existujú aj kreatívne úlohy:

Príklad 7

Pri akej hodnote parametra budú vektory koplanárne?

rozhodnutie: Vektory sú koplanárne vtedy a len vtedy, ak sa determinant zložený zo súradníc daných vektorov rovná nule:

V podstate musíte vyriešiť rovnicu s determinantom. Letíme do núl ako šarkani do jerbov - najvýhodnejšie je otvoriť determinant v druhom riadku a okamžite sa zbaviť mínusov:

Vykonávame ďalšie zjednodušenia a redukujeme záležitosť na najjednoduchšiu lineárnu rovnicu:

Odpoveď: o

Tu je ľahké to skontrolovať, preto musíte výslednú hodnotu nahradiť pôvodným determinantom a uistiť sa jej opätovným otvorením.

Na záver sa zamyslime nad ďalším typickým problémom, ktorý má skôr algebraický charakter a je tradične súčasťou kurzu lineárnej algebry. Je taký rozšírený, že si zaslúži samostatnú tému:

Dokážte, že 3 vektory tvoria základ trojrozmerného priestoru
a nájdite súradnice 4. vektora v danom základe

Príklad 8

Sú uvedené vektory. Ukážte, že vektory tvoria základ trojrozmerného priestoru a nájdite súradnice vektora v tomto základe.

rozhodnutie: Poďme sa najskôr zaoberať podmienkou. Podľa podmienky sú dané štyri vektory, a ako vidíte, už majú súradnice na nejakom základe. Čo je základ - nezaujíma nás. A nasledujúca vec je zaujímavá: tri vektory môžu dobre tvoriť nový základ. A prvý krok je úplne rovnaký ako pri riešení príkladu 6, je potrebné skontrolovať, či sú vektory skutočne lineárne nezávislé:

Vypočítajte determinant zložený zo súradníc vektorov:

vektory sú teda lineárne nezávislé a tvoria základ trojrozmerného priestoru.

! Dôležité : vektorové súradnice nevyhnutne zapísať do stĺpcov determinant, nie reťazce. V opačnom prípade nastane zmätok v ďalšom algoritme riešenia.

V geometrii sa vektor chápe ako riadený segment a vektory získané jeden od druhého paralelnou transláciou sa považujú za rovnocenné. Všetky rovnaké vektory sa považujú za rovnaký vektor. Začiatok vektora môže byť umiestnený v akomkoľvek bode priestoru alebo roviny.

Ak sú súradnice koncov vektora uvedené v priestore: A(X 1 , r 1 , z 1), B(X 2 , r 2 , z 2), potom

= (X 2 – X 1 , r 2 – r 1 , z 2 – z 1). (1)

Podobný vzorec platí aj v rovine. To znamená, že vektor možno zapísať ako súradnicový reťazec. Operácie s vektormi, - sčítanie a násobenie číslom, na reťazcoch sa vykonávajú komponent po komponente. To umožňuje rozšíriť koncept vektora, chápať vektor ako akýkoľvek reťazec čísel. Napríklad riešenie systému lineárnych rovníc, ako aj akejkoľvek množiny hodnôt systémových premenných, možno považovať za vektor.

Na reťazcoch rovnakej dĺžky sa operácia sčítania vykonáva podľa pravidla

(a 1, a 2, …, a n) + (b1, b2, …, b n) = (a 1 + b 1, a 2 + b 2, …, a n+b n). (2)

Násobenie reťazca číslom sa vykonáva podľa pravidla

l(a 1, a 2, …, a n) = (la 1, la 2, …, la n). (3)

Sada riadkových vektorov danej dĺžky n s naznačenými operáciami vektorového sčítania a násobenia číslom tvorí algebraickú štruktúru tzv n-rozmerný lineárny priestor.

Lineárna kombinácia vektorov je vektor , kde λ 1 , ... , λ m sú ľubovoľné koeficienty.

Systém vektorov sa nazýva lineárne závislý, ak existuje jeho lineárna kombinácia rovná , ktorá má aspoň jeden nenulový koeficient.

Systém vektorov sa nazýva lineárne nezávislý, ak v ktorejkoľvek z jeho lineárnych kombinácií rovných sú všetky koeficienty nulové.

Tým sa riešenie otázky lineárnej závislosti sústavy vektorov redukuje na riešenie rovnice

X 1 + X 2 + … + x m = . (4)

Ak má táto rovnica nenulové riešenia, potom je systém vektorov lineárne závislý. Ak je nulové riešenie jedinečné, potom je systém vektorov lineárne nezávislý.

Aby sme vyriešili systém (4), pre prehľadnosť môžu byť vektory zapísané nie vo forme riadkov, ale vo forme stĺpcov.

Potom, po vykonaní transformácií na ľavej strane, dospejeme k sústave lineárnych rovníc ekvivalentnej rovnici (4). Hlavná matica tohto systému je tvorená súradnicami pôvodných vektorov usporiadaných do stĺpcov. Stĺpec voľných členov tu nie je potrebný, pretože systém je homogénny.

Základ systém vektorov (konečný alebo nekonečný, najmä celý lineárny priestor) je jeho neprázdny lineárne nezávislý podsystém, prostredníctvom ktorého možno vyjadriť ľubovoľný vektor systému.

Príklad 1.5.2. Nájdite základ sústavy vektorov = (1, 2, 2, 4), = (2, 3, 5, 1), = (3, 4, 8, –2), = (2, 5, 0, 3) a prostredníctvom bázy vyjadrujú ďalšie vektory.

rozhodnutie. Zostavíme maticu, v ktorej sú súradnice týchto vektorov usporiadané do stĺpcov. Toto je matica systému X 1 + X 2 + X 3 + X 4 =. . Maticu uvedieme do stupňovitého tvaru:

~ ~ ~

Základ tohto systému vektorov tvoria vektory , , , ktoré zodpovedajú vodiacim prvkom riadkov označených krúžkami. Na vyjadrenie vektora riešime rovnicu X 1 + X 2 + X 4 = . Redukuje sa na sústavu lineárnych rovníc, ktorých maticu získame z originálu preusporiadaním stĺpca zodpovedajúceho , na miesto stĺpca voľných členov. Preto pri redukcii na stupňovitú formu sa na matici vykonajú rovnaké transformácie ako vyššie. To znamená, že výslednú maticu môžeme použiť v stupňovitej forme vykonaním potrebných permutácií stĺpcov v nej: stĺpce s kruhmi sú umiestnené naľavo od zvislej čiary a stĺpec zodpovedajúci vektoru je umiestnený vpravo. z baru.

Postupne nachádzame:

X 4 = 0;

X 2 = 2;

X 1 + 4 = 3, X 1 = –1;

Komentujte. Ak je potrebné prostredníctvom bázy vyjadriť niekoľko vektorov, potom sa pre každý z nich zostrojí zodpovedajúci systém lineárnych rovníc. Tieto systémy sa budú líšiť len v stĺpcoch voľných členov. V tomto prípade je každý systém riešený nezávisle od ostatných.

CVIČENIE 1.4. Nájdite základ systému vektorov a vyjadrite zvyšok vektorov pomocou základu:

a) = (1, 3, 2, 0), = (3, 4, 2, 1), = (1, –2, –2, 1), = (3, 5, 1, 2);

b) = (2, 1, 2, 3), = (1, 2, 2, 3), = (3, –1, 2, 2), = (4, –2, 2, 2);

c) = (1, 2, 3), = (2, 4, 3), = (3, 6, 6), = (4, –2, 1); = (2, -6, -2).

V danom systéme vektorov možno bázu zvyčajne rozlíšiť rôznymi spôsobmi, ale všetky bázy budú mať rovnaký počet vektorov. Počet vektorov v základe lineárneho priestoru sa nazýva dimenzia priestoru. Pre n-rozmerný lineárny priestor n je rozmer priestoru, keďže tento priestor má štandardný základ = (1, 0, … , 0), = (0, 1, … , 0), … , = (0, 0, … , 1). Prostredníctvom tohto základu je ľubovoľný vektor = (a 1 , a 2 , … , a n) sa vyjadruje takto:

= (a 1 , 0, … , 0) + (0, a 2, … , 0) + … + (0, 0, … , a n) =

A 1 (1, 0, …, 0) + a 2 (0, 1, …, 0) + … + a n(0, 0, ... ,1) = a 1 + a 2 + ... + a n .

Teda zložky v riadku vektora = (a 1 , a 2 , … , a n) sú jeho koeficienty v expanzii v zmysle štandardného základu.

Priame čiary v rovine

Problémom analytickej geometrie je aplikácia súradnicovej metódy na geometrické úlohy. Úloha je teda prevedená do algebraickej formy a vyriešená pomocou algebry.

Nájdite základ systému vektorov a vektorov, ktoré nie sú zahrnuté v základe, rozviňte na základe:

a 1 = {5, 2, -3, 1}, a 2 = {4, 1, -2, 3}, a 3 = {1, 1, -1, -2}, a 4 = {3, 4, -1, 2}, a 5 = {13, 8, -7, 4}.

rozhodnutie. Uvažujme homogénny systém lineárnych rovníc

a 1 X 1 + a 2 X 2 + a 3 X 3 + a 4 X 4 + a 5 X 5 = 0

alebo rozšírené.

Tento systém vyriešime Gaussovou metódou, bez prehadzovania riadkov a stĺpcov a navyše výberom hlavného prvku nie v ľavom hornom rohu, ale v celom riadku. Úlohou je vyberte diagonálnu časť transformovanej sústavy vektorov.

~ ~

~ ~ ~ .

Povolený systém vektorov, ktorý je ekvivalentný pôvodnému, má tvar

a 1 1 X 1 + a 2 1 X 2 + a 3 1 X 3 + a 4 1 X 4 + a 5 1 X 5 = 0 ,

kde a 1 1 = , a 2 1 = , a 3 1 = , a 4 1 = , a 5 1 = . (1)

vektory a 1 1 , a 3 1 , a 4 1 tvoria diagonálny systém. Preto tie vektory a 1 , a 3 , a 4 tvoria základ sústavy vektorov a 1 , a 2 , a 3 , a 4 , a 5 .

Teraz rozšírime vektory a 2 a a 5 v základe a 1 , a 3 , a 4. Aby sme to dosiahli, najprv rozšírime príslušné vektory a 2 1 a a 5 1 diagonálny systém a 1 1 , a 3 1 , a 4 1, berúc do úvahy, že koeficienty rozšírenia vektora v diagonálnom systéme sú jeho súradnice x i.

Z (1) máme:

a 2 1 = a 31 (-1) + a 4 1 0 + a 1 1 1 a 2 1 = a 1 1 – a 3 1 .

a 5 1 = a 3 1 0 + a 4 1 1+ a 1 1 2 a 5 1 = 2a 1 1 + a 4 1 .

vektory a 2 a a 5 rozšíriť v základe a 1 , a 3 , a 4 s rovnakými koeficientmi ako vektory a 2 1 a a 5 1 diagonálny systém a 1 1 , a 3 1 , a 4 1 (tie koeficienty x i). teda

a 2 = a 1 – a 3 , a 5 = 2a 1 + a 4 .

Úlohy. jeden.Nájdite základ sústavy vektorov a vektory, ktoré nie sú zahrnuté v základe, rozviňte podľa základu:

1. a 1 = { 1, 2, 1 }, a 2 = { 2, 1, 3 }, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4 }.

2. a 1 = { 1, 1, 2 }, a 2 = { 0, 1, 2 }, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0 }.

3. a 1 = { 1, -2, 3 }, a 2 = { 0, 1, -1 }, a 3 = { 1, 3, 0 }, a 4 = { 0, -7, 3 }, a 5 = { 1, 1, 1 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

2. Nájdite všetky základy systému vektorov:

1. a 1 = { 1, 1, 2 }, a 2 = { 3, 1, 2 }, a 3 = { 1, 2, 1 }, a 4 = { 2, 1, 2 }.

2. a 1 = { 1, 1, 1 }, a 2 = { -3, -5, 5 }, a 3 = { 3, 4, -1 }, a 4 = { 1, -1, 4 }.