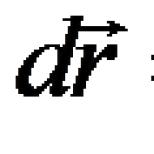Neobmedzená funkcia. Obmedzenie funkcie. Funkcia vzostupne a zostupne

Všimnite si, že všetky definície obsahujú číselnú množinu X, ktorá je súčasťou domény funkcie: X s D(f). V praxi sa najčastejšie vyskytujú prípady, keď X je číselný interval (segment, interval, lúč atď.).

Definícia 1.

Funkcia y \u003d f (x) sa nazýva rastúca na množine X s D (f), ak pre ľubovoľné dva body x 1 a x 2 množiny X tak, že x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).

Definícia 2.

Funkcia y \u003d f (x) sa nazýva klesajúca na množine X s D (f), ak pre akúkoľvek monotónnosť dvoch bodov x 1 a x 2 množiny X tak, že x 1< х 2 , функции выполняется неравенство f(x 1) >f(x2).

V praxi je vhodnejšie použiť nasledujúce formulácie: funkcia sa zvyšuje, ak väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie; funkcia je klesajúca, ak väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

V 7. a 8. ročníku sme použili nasledujúcu geometrickú interpretáciu pojmov rastúcich alebo klesajúcich funkcií: pohybom po grafe rastúcej funkcie zľava doprava akosi stúpame do kopca (obr. 55); pohybom po grafe klesajúcej funkcie zľava doprava, ako keby sme išli z kopca (obr. 56).
Pojmy „rastúca funkcia“, „klesajúca funkcia“ sú zvyčajne spojené spoločným názvom monotónna funkcia a štúdium funkcie na zvýšenie alebo zníženie sa nazýva štúdium funkcie na monotónnosť.

Všimnime si ešte jednu okolnosť: ak funkcia rastie (alebo klesá) vo svojom prirodzenom obore, potom sa zvyčajne hovorí, že funkcia rastie (alebo klesá) - bez uvedenia číselnej množiny X.

Príklad 1

Preskúmajte monotónnosť funkcie:

a) y \u003d x 3 + 2; b) y \u003d 5 - 2x.

rozhodnutie:

a) Vezmite ľubovoľné hodnoty argumentu x 1 a x 2 a nech x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

Posledná nerovnosť znamená, že f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).

Takže od x 1< х 2 следует f(х 1) >f(x 2), čo znamená, že daná funkcia je klesajúca (na celej číselnej osi).

Definícia 3.

Funkcia y - f(x) sa nazýva ohraničená zdola na množine X s D (f), ak sú všetky hodnoty funkcie na množine X väčšie ako určité číslo (inými slovami, ak existuje číslo m také, že pre ľubovoľnú hodnotu x є X je nerovnosť f( x) >m).

Definícia 4.

Funkcia y \u003d f (x) sa nazýva ohraničená zhora na množine X s D (f), ak sú všetky hodnoty funkcie menšie ako určité číslo (inými slovami, ak existuje číslo M také, že pre akúkoľvek hodnotu x є X nerovnosť f (x)< М).

Ak množina X nie je špecifikovaná, potom sa predpokladá, že funkcia je ohraničená zdola alebo zhora v celom definičnom obore.

Ak je funkcia ohraničená zdola aj zhora, potom sa nazýva ohraničená.

Ohraničenosť funkcie sa dá ľahko prečítať z jej grafu: ak je funkcia ohraničená zdola, potom je jej graf celý umiestnený nad nejakou vodorovnou čiarou y \u003d m (obr. 57); ak je funkcia ohraničená zhora, potom je jej graf celý umiestnený pod vodorovnou čiarou y \u003d M (obr. 58).

Príklad 2 Preskúmajte ohraničenosť funkcie
rozhodnutie. Na jednej strane je nerovnosť celkom zjavná (podľa definície odmocniny to znamená, že funkcia je ohraničená zdola. Na druhej strane máme a teda
To znamená, že funkcia je ohraničená zhora. Teraz sa pozrite na graf danej funkcie (obr. 52 z predchádzajúceho odseku). Ohraničenosť funkcie zhora aj zdola sa z grafu odčítava celkom jednoducho.

Definícia 5.

Číslo m sa nazýva najmenšia hodnota funkcie y \u003d f (x) na množine X C D (f), ak:

1) v X je taký bod x 0, že f(x 0) = m;

2) pre všetky x z X je splnená nerovnosť m>f(х 0).

Definícia 6.

Číslo M sa nazýva najväčšia hodnota funkcie y \u003d f (x) na množine X C D (f), ak:
1) v X je taký bod x 0, že f(x 0) = M;
2) pre všetky x z X, nerovnosť
Najmenšiu hodnotu funkcie sme v 7. aj 8. ročníku označovali symbolom y a najväčšiu hodnotu symbolom y.

Ak množina X nie je špecifikovaná, potom sa predpokladá, že hovoríme o nájdení najmenšej alebo najväčšej hodnoty funkcie v celom definičnom obore.

Nasledujúce užitočné vyhlásenia sú celkom zrejmé:

1) Ak má funkcia Y, potom je ohraničená zdola.
2) Ak má funkcia Y, potom je zhora ohraničená.
3) Ak funkcia nie je ohraničená nižšie, potom Y neexistuje.
4) Ak funkcia nie je zhora ohraničená, potom Y neexistuje.

Príklad 3

Nájdite najmenšie a najväčšie hodnoty funkcie
rozhodnutie.

Je celkom zrejmé, najmä ak sa uchýlite k funkčnému grafu (obr. 52), že \u003d 0 (funkcia dosiahne túto hodnotu v bodoch x \u003d -3 a x \u003d 3), a \u003d 3 ( funkcia dosiahne túto hodnotu v bode x \u003d 0.
V 7. a 8. ročníku sme spomenuli ešte dve vlastnosti funkcií. Prvá sa nazývala vlastnosť konvexnosti funkcie. Predpokladá sa, že funkcia je konvexná smerom nadol na intervale X, ak spojením ľubovoľných dvoch bodov jej grafu (s úsečkami z X) s úsečkou priamky zistíme, že zodpovedajúca časť grafu leží pod nakreslenou úsečkou ( Obr. 59). spojitosť Funkcia je konvexná smerom nahor na intervale X, ak spojením ľubovoľných dvoch bodov jej grafu (s x x) priamkou úsečkou zistíme, že zodpovedajúca časť grafu leží nad nakreslenou úsečkou (obr. 60). ).

Druhá vlastnosť – spojitosť funkcie na intervale X – znamená, že graf funkcie na intervale X je spojitý, t.j. nemá žiadne vpichy a skoky.

Komentujte.

V matematike je v skutočnosti všetko, ako sa hovorí, „presne naopak“: graf funkcie sa zobrazuje ako plná čiara (bez vpichov a skokov) iba vtedy, keď je dokázaná kontinuita funkcie. Formálna definícia kontinuity funkcie, ktorá je pomerne zložitá a jemná, je však zatiaľ nad naše sily. To isté možno povedať o konvexnosti funkcie. Pri diskusii o týchto dvoch vlastnostiach funkcií sa budeme aj naďalej spoliehať na vizuálne intuitívne reprezentácie.

Teraz si zopakujme naše vedomosti. Pri spomienke na funkcie, ktoré sme študovali v 7. a 8. ročníku, si objasníme, ako vyzerajú ich grafy a vymenujeme vlastnosti funkcie, dodržujúc určité poradie, napr.: doména definície; monotónna; obmedzenie; , ; kontinuita; rozsah hodnôt; konvexné.

Následne sa objavia nové vlastnosti funkcií a podľa toho sa zmení aj zoznam vlastností.

1. Konštantná funkcia y \u003d C

Graf funkcie y \u003d C je znázornený na obr. 61 - priamka, rovnobežná s osou x. Ide o natoľko nezaujímavú funkciu, že nemá zmysel uvádzať jej vlastnosti.

Graf funkcie y \u003d kx + m je priamka (obr. 62, 63).

Vlastnosti funkcie y \u003d kx + m:

1)
2) rastie, ak k > 0 (obr. 62), klesá, ak k< 0 (рис. 63);

4) neexistujú ani najväčšie, ani najmenšie hodnoty;
5) funkcia je spojitá;
6)
7) nemá zmysel hovoriť o konvexnosti.

Graf funkcie y \u003d kx 2 je parabola s vrcholom v počiatku a s vetvami smerujúcimi nahor, ak k\u003e O (obr. 64), a nadol, ak k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Vlastnosti funkcie y - kx 2:

Pre prípad k > 0 (obr. 64):

1) D(f) = (-oo,+oo);


4) = neexistuje;
5) kontinuálne;
6) Е(f) = funkcia klesá a na intervale klesá na lúči;
7) konvexné smerom nahor.

Graf funkcie y \u003d f (x) je zostavený bod po bode; čím viac bodov tvaru (x; f (x)) vezmeme, tým presnejšiu predstavu o grafe získame. Ak vezmeme veľa z týchto bodov, potom bude myšlienka grafu úplnejšia. Práve v tomto prípade nám intuícia hovorí, že graf treba nakresliť ako plnú čiaru (v tomto prípade ako parabolu). A potom pri čítaní grafu vyvodíme závery o spojitosti funkcie, o jej konvexnosti smerom nadol alebo nahor, o rozsahu funkcie. Musíte pochopiť, že z uvedených siedmich vlastností sú len vlastnosti 1), 2), 3), 4) „legálne“ v tom zmysle, že ich dokážeme podložiť odvolaním sa na presné definície. O zostávajúcich vlastnostiach máme len vizuálne-intuitívne znázornenia. Mimochodom, nie je na tom nič zlé. Z histórie vývoja matematiky je známe, že ľudstvo často a dlho využívalo rôzne vlastnosti určitých predmetov, pričom nepoznalo presné definície. Potom, keď sa dali sformulovať takéto definície, všetko do seba zapadlo.

Grafom funkcie je hyperbola, súradnicové osi slúžia ako asymptoty hyperboly (obr. 66, 67).

1) D(f) = (-00,0)1U (0,+oo);
2) ak k > 0, potom funkcia klesá na otvorenom lúči (-oo, 0) a na otvorenom lúči (0, +oo) (obr. 66); ak do< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) nie je obmedzený ani zdola, ani zhora;
4) neexistujú ani najmenšie, ani najväčšie hodnoty;
5) funkcia je spojitá na otvorenom lúči (-oo, 0) a na otvorenom lúči (0, +oo);
6) E(f) = (-oo, 0) U (0, + oo);
7) ak k > 0, potom je funkcia konvexná smerom nahor v x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, t.j. na otvorenom nosníku (0, +oo) (obr. 66). Ak do< 0, то функция выпукла вверх при х >o a konvexné nadol v x< О (рис. 67).
Grafom funkcie je vetva paraboly (obr. 68). Vlastnosti funkcie:
1) D(f) = , narastá na lúči a je diferencovateľný v intervale ( a;b), potom je tu taký bod, že

Cauchyho veta.

Ak sú funkcie f(x) a g(x) spojité na intervale a diferencovateľné na intervale (a, b) a g¢(x) ¹ 0 na intervale (a, b), potom existuje aspoň jeden bod e, a< e < b, такая, что

Tie. pomer prírastkov funkcií na danom segmente sa rovná pomeru derivácií v bode e. Príklady riešenia úloh prednáškový kurz Výpočet objemu telesa zo známych oblastí jeho rovnobežných rezov Integrálny počet

Príklady práce v kurze elektrotechnika

Na dôkaz tejto vety je na prvý pohľad veľmi vhodné použiť Lagrangeovu vetu. Napíšte vzorec konečného rozdielu pre každú funkciu a potom ich navzájom vydeľte. Tento názor je však mylný, pretože bod e pre každú z funkcií je vo všeobecnosti iný. Samozrejme, v niektorých špeciálnych prípadoch môže byť tento intervalový bod rovnaký pre obe funkcie, ale je to veľmi zriedkavá zhoda okolností, nie pravidlo, a preto sa nedá použiť na dokázanie vety.

Dôkaz. Zvážte funkciu pomocníka

Keď x→x 0, hodnota c má tiež tendenciu k x 0; prejdime v predchádzajúcej rovnosti na limit:

Ako , potom .

Takže

(limita pomeru dvoch infinitezimál sa rovná limite pomeru ich derivácií, ak druhá existuje)

L'Hopitalovo pravidlo pri ∞ / ∞.

Veta o limite monotónnej funkcie. Dôkaz vety sa podáva dvoma spôsobmi. Uvádzajú sa aj definície prísne rastúcich, neklesajúcich, prísne klesajúcich a nezvyšujúcich sa funkcií. Definícia monotónnej funkcie.

Funkcia nie je zhora obmedzená

1.1. Nech je číslo b konečné: .
1.1.2. Nech je funkcia zhora neobmedzená.

.

v .

Označme . Potom pre akékoľvek existuje , takže
v .
To znamená, že limita vľavo v bode b je (pozri "Definície jednostranných nekonečných limitov funkcie v koncovom bode").

b skoré plus nekonečno

Funkcia obmedzená zhora

1. Nech funkcia neklesá na intervale .
1.2.1. Nech je funkcia zhora ohraničená číslom M : pre .
Dokážme, že v tomto prípade existuje limit.

Keďže funkcia je ohraničená zhora, existuje konečná horná hranica
.
Podľa definície najmenšej hornej hranice sú splnené tieto podmienky:
;
pre každé pozitívum existuje argument, pre ktorý
.

Keďže funkcia neklesá, potom pre . Potom o . Alebo
v .

Takže sme zistili, že pre ľubovoľnú existuje číslo , takže
v .
"Definície jednostranných limitov v nekonečne").

Funkcia nie je zhora obmedzená

1. Nech funkcia neklesá na intervale .
1.2. Nech je číslo b plus nekonečno: .
1.2.2. Nech je funkcia zhora neobmedzená.
Dokážme, že v tomto prípade existuje limit.

Keďže funkcia nie je zhora ohraničená, potom pre ľubovoľné číslo M existuje argument , pre ktorý
.

Keďže funkcia neklesá, potom pre . Potom o .

Takže pre všetky existuje číslo , takže
v .
To znamená, že limit v je (pozri "Definície jednostranných nekonečných limitov v nekonečne").

Funkcia sa nezvýši

Teraz zvážte prípad, keď sa funkcia nezvyšuje. Ako je uvedené vyššie, môžete zvážiť každú možnosť samostatne. Ale hneď ich zakryjeme. Na to používame. Dokážme, že v tomto prípade existuje limit.

Zvážte konečnú dolnú hranicu množiny funkčných hodnôt:
.
Tu B môže byť buď konečné číslo, alebo bod v nekonečne. Podľa definície presného infimu sú splnené tieto podmienky:
;
pre akékoľvek okolie bodu B existuje argument, pre ktorý
.
Podľa podmienky vety, . Takže .

Keďže funkcia sa nezvýši, potom pre . Pretože teda
v .
Alebo
v .
Ďalej si všimneme, že nerovnosť definuje ľavé prepichnuté okolie bodu b .

Zistili sme teda, že pre každé okolie bodu existuje také prepichnuté ľavé okolie bodu b, že
v .
To znamená, že limit vľavo v bode b je:

(pozri univerzálnu definíciu limity funkcie podľa Cauchyho).

Limit v bode a

Teraz ukážme, že v bode a je limita a nájdime jej hodnotu.

Uvažujme o funkcii. Podľa podmienky vety je funkcia monotónna pre . Nahraďte premennú x za - x (alebo urobte substitúciu a potom nahraďte premennú t za x ). Potom je funkcia monotónna pre . Násobenie nerovností o -1 a zmenou ich poradia dospejeme k záveru, že funkcia je monotónna pre .

Podobným spôsobom sa dá ľahko ukázať, že ak neklesá, tak nerastie. Potom, podľa toho, čo bolo dokázané vyššie, existuje hranica
.
Ak sa nezvýši, tak sa nezníži. V tomto prípade existuje limit
.

Teraz zostáva ukázať, že ak existuje limita funkcie v , potom existuje limita funkcie v , a tieto limity sú rovnaké:
.

Predstavme si notáciu:
(1) .
Vyjadrime f pomocou g :
.
Vezmite ľubovoľné kladné číslo. Nech existuje epsilon okolie bodu A . Okolie Epsilon je definované pre konečné aj nekonečné hodnoty A (pozri „Okolie bodu“). Keďže existuje limita (1), potom podľa definície limity pre akúkoľvek existuje taká, že
v .

Nech a je konečné číslo. Vyjadrime ľavé prepichnuté okolie bodu -a pomocou nerovností:
v .
Nahradme x za -x a vezmime do úvahy, že:
v .
Posledné dve nerovnosti definujú prepichnuté pravé okolie bodu a . Potom
v .

Nech a je nekonečné číslo, . Opakujeme diskusiu.
v ;
v ;
v ;
v .

Takže sme zistili, že pre každú existuje taká, že
v .
Znamená to, že
.

Veta bola dokázaná.

Na množine A z domény D(f) budeme volať funkciu y=f(x) ZAHRNUTÉ (DNO), ak také číslo existuje. M , že pre ľubovoľné x z tohto nastavte podmienku

Pomocou logických symbolov možno definíciu zapísať takto:

f(x) – ohraničené zhora na scéne

(f(x) – ohraničené zospodu na scéne

Do úvahy sa berú aj funkcie ohraničené v absolútnej hodnote alebo jednoducho ohraničené.

Funkciu OBMEDZENÚ na množine A zavoláme z definičného oboru, ak existuje kladné číslo M také, že

V jazyku logických symbolov

f(x) – obmedzené na súprave

Funkcia, ktorá nie je ohraničená, sa nazýva neohraničená. Vieme, že definície dané negáciou majú malý obsah. Na formulovanie tohto tvrdenia ako definície používame vlastnosti kvantifikátorových operácií (3.6) a (3.7). Potom odmietnutie ohraničenosti funkcie v jazyku logických symbolov poskytne:

f(x) – obmedzené na súprave

Získaný výsledok nám umožňuje sformulovať nasledujúcu definíciu.

Funkcia sa nazýva NEOBMEDZENÁ na množine A, ktorá patrí do definičného oboru funkcie, ak na tejto množine pre ľubovoľné kladné číslo M existuje taká hodnota argumentu x , že hodnota bude stále prevyšovať hodnotu M, teda .

Ako príklad zvážte funkciu

Je definovaný na celej skutočnej osi. Ak vezmeme segment [–2;1] (množina A), bude na ňom ohraničený zhora aj zdola.

V skutočnosti, aby sme ukázali, že je ohraničený zhora, musíme zvážiť predikát

a ukážte, že existuje (existuje) M tak, že pre všetky x prijaté na segmente [–2;1] bude platiť

Nájsť takého M nie je ťažké. Môžeme predpokladať M = 7, kvantifikátor existencie znamená nájsť aspoň jednu hodnotu M. Prítomnosť takéhoto M potvrdzuje skutočnosť, že funkcia na segmente [–2;1] je zhora ohraničená.

Aby sme dokázali jeho ohraničenosť zdola, musíme zvážiť predikát

Hodnota M, ktorá zabezpečuje pravdivosť tohto predikátu, je napríklad M = -100.

Dá sa dokázať, že funkcia bude ohraničená aj modulo: pre všetky x zo segmentu [–2;1] sa hodnoty funkcie zhodujú s hodnotami , preto ako M môžeme vziať , napríklad predchádzajúca hodnota M = 7.

Ukážme, že tá istá funkcia, ale na intervale , bude neohraničená, tj.

Ak chcete ukázať, že také x existuje, zvážte tento výrok

Vyhľadaním požadovaných hodnôt x medzi kladnými hodnotami argumentu dostaneme

To znamená, že bez ohľadu na to, aké pozitívne Mwe vezmeme, hodnoty x zabezpečujú splnenie nerovnosti

sa získajú z pomeru.

Ak vezmeme do úvahy funkciu na celej reálnej osi, môžeme ukázať, že je neobmedzená v absolútnej hodnote.

Naozaj, z nerovnosti

To znamená, že bez ohľadu na to, aké veľké je kladné M, alebo zabezpečí splnenie nerovnosti .

EXTRÉMNA FUNKCIA.

Funkcia má v bode s miestne maximum (minimum), ak existuje také okolie tohto bodu, že pre X¹ s toto okolie spĺňa nerovnosť

najmä, že extrémny bod môže byť iba vnútorným bodom medzery a musí v ňom byť definovaná f(x). Možné prípady absencie extrému sú znázornené na obr. 8.8.

Ak sa funkcia v určitom intervale zvyšuje (klesá) a v určitom intervale klesá (zvyšuje sa), potom bod s je lokálny maximálny (minimálny) bod.

Neprítomnosť maxima funkcie f(x) v bode s možno formulovať takto:

_______________________

f(x) má maximum v c

To znamená, že ak bod c nie je lokálnym maximálnym bodom, potom bez ohľadu na to, aké okolie obsahuje bod c ako vnútorné, existuje aspoň jedna hodnota x, ktorá sa nerovná c, pre ktorú platí . Ak teda v bode c nie je maximum, potom v tomto bode nemusí byť extrém vôbec, alebo to môže byť minimálny bod (obr. 8.9).

Koncept extrému poskytuje komparatívne hodnotenie hodnoty funkcie v akomkoľvek bode vo vzťahu k blízkym. Podobné porovnanie funkčných hodnôt je možné vykonať pre všetky body určitého intervalu.

NAJVÄČŠIA (MINIMÁLNA) hodnota funkcie v množine je jej hodnota v bode z tejto množiny tak, že – pre . Najväčšia hodnota funkcie sa dosiahne vo vnútornom bode segmentu a najmenšia – na jeho ľavom konci.

Na určenie najväčšej (najmenšej) hodnoty funkcie danej na segmente je potrebné vybrať najväčšie (najmenšie) číslo spomedzi všetkých hodnôt jej maxím (minimál), ako aj hodnôt získaných pri konce intervalu. Bude to najväčšia (najmenšia) hodnota funkcie. Toto pravidlo bude špecifikované neskôr.

Problém hľadania najväčších a najmenších hodnôt funkcie na otvorenom intervale nie je vždy ľahko vyriešený. Napríklad funkcia

v intervale (obr. 8.11) ich nemá.

Uistime sa napríklad, že táto funkcia nemá najväčšiu hodnotu. Vzhľadom na monotónnosť funkcie možno skutočne tvrdiť, že bez ohľadu na to, ako blízko nastavíme hodnoty x naľavo od jednoty, bude existovať ďalšie x, v ktorom budú hodnoty funkcie väčšie ako jeho hodnoty v daných pevných bodoch, ale stále menšie ako jednota.