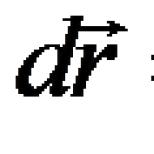Podmienka lineárnej nezávislosti vektorov. Lineárna závislosť a nezávislosť lineárnych priestorových vektorov. Lineárna závislosť a nezávislosť trojrozmerných priestorových vektorov. Priestorová báza a afinný súradnicový systém

Definícia 18.2 Funkčný systémf, ..., f pvolalli-nape o h a in a c a m. o d v medzere(a, (3) ak nejaké netriviálne 5 lineárna kombinácia týchto funkcií sa rovná nule na tomto intervale zhodne:

Definícia 18.3 Vektorový systém f 1, ..., x n sa nazýva lineárne v a a c a m o d, ak sa nejaká netriviálna lineárna kombinácia týchto vektorov rovná vektoru odrážky:

L Aby nedošlo k zámene, označíme číslo zložky vektora (vektor-funkcia) spodným indexom a číslo samotného vektora (ak je takýchto vektorov viacero) horným.

„Pripomíname, že lineárna kombinácia sa nazýva netriviálna, ak v nej nie sú všetky koeficienty nulové.

Definícia 18.4 Systém vektorových funkcií x 1 ^),..., x n (t) sa nazýva lineárny h a dnu a s a mojim asi th na intervale,(a, /3) ak sa nejaká netriviálna lineárna kombinácia týchto vektorových funkcií zhodne rovná nulovému vektoru na tomto intervale:

Je dôležité pochopiť prepojenie týchto troch pojmov (lineárna závislosť funkcií, vektorov a vektorových funkcií) medzi sebou.

V prvom rade, ak predložíme vzorec (18.6) v rozšírenej forme (pamätajúc na to, že každý z x g (1) je vektor)

potom to bude ekvivalentné systému rovnosti

čo znamená lineárnu závislosť r-tých zložiek v zmysle prvej definície (ako funkcie). Hovorí sa, že lineárna závislosť vektorových funkcií implikuje ich komponent po komponente lineárna závislosť.

Opak vo všeobecnosti neplatí: stačí zvážiť príklad dvojice vektorových funkcií

Prvé zložky týchto vektorových funkcií sa jednoducho zhodujú, čo znamená, že sú lineárne závislé. Druhé zložky sú proporcionálne, tzv. sú tiež lineárne závislé. Ak sa však pokúsime zostrojiť ich lineárnu kombináciu rovnú nule identicky, tak zo vzťahu

okamžite získajte systém

čo má jediné riešenie C - C-2 - 0. Naše vektorové funkcie sú teda lineárne nezávislé.

Aký je dôvod takejto zvláštnej vlastnosti? Aký je trik, ktorý vám umožňuje zostaviť lineárne nezávislé vektorové funkcie z vedome závislých funkcií?

Ukazuje sa, že celý bod nie je ani tak v lineárnej závislosti komponentov, ale v pomere koeficientov, ktorý je potrebný na získanie nuly. V prípade lineárnej závislosti vektorových funkcií slúži rovnaká množina koeficientov všetkým komponentom bez ohľadu na počet. Ale v našom príklade bol pre jeden komponent potrebný jeden pomer koeficientov a pre druhý iný. Takže trik je vlastne jednoduchý: na získanie lineárnej závislosti celých vektorových funkcií z lineárnej závislosti „komponent po komponente“ je potrebné, aby všetky komponenty boli lineárne závislé „v rovnakom pomere“.

Prejdime teraz k štúdiu vzťahu medzi lineárnou závislosťou vektorových funkcií a vektorov. Tu je takmer zrejmé, že lineárna závislosť vektorových funkcií znamená, že pre každú je pevná t* vektor

bude lineárne závislá.

Opak, všeobecne povedané, neplatí: z lineárnej závislosti vektorov pre každý t nesleduje lineárnu závislosť vektorových funkcií. To je dobre vidieť na príklade dvoch vektorových funkcií

o t = 1, t = 2 a t = 3 dostaneme dvojice vektorov

resp. Každý pár vektorov je proporcionálny (s koeficientmi 1, 2 a 3). Je ľahké vidieť, že pre všetky pevné t* naša dvojica vektorov bude úmerná koeficientu t*.

Ak sa pokúsime zostrojiť lineárnu kombináciu vektorových funkcií, ktorá sa identicky rovná nule, prvé zložky nám už dávajú vzťah

čo je možné len vtedy S = S2 = 0. Naše vektorové funkcie sa teda ukázali ako lineárne nezávislé. Vysvetlenie tohto efektu je opäť také, že v prípade lineárnej závislosti vektorových funkcií slúži všetkým hodnotám rovnaká množina konštánt Cj t, a v našom príklade pre každú hodnotu t si vyžiadal vlastný pomer medzi koeficientmi.

Nech funkcie , majú derivácie limity (n-1).

Zvážte determinant: (1)

W(x) sa nazýva Wronského determinant pre funkcie .

Veta 1. Ak sú funkcie v intervale (a, b) lineárne závislé, tak ich Wronskian W(x) je v tomto intervale zhodne rovný nule.

Dôkaz. Podmienkou vety, vzťahu

, (2) kde nie všetky sa rovnajú nule. Nechať byť. Potom

(3). Diferencujte túto identitu n-1 krát a

Nahradením ich získaných hodnôt do Vronského determinantu,

dostaneme:

(4).

Vo Wronského determinante je posledný stĺpec lineárnou kombináciou predchádzajúcich n-1 stĺpcov a je teda nulový vo všetkých bodoch intervalu (a, b).

Veta 2. Ak funkcie y1,…, yn sú lineárne nezávislé riešenia rovnice L[y] = 0, ktorých všetky koeficienty sú spojité v intervale (a, b), potom je Wronskian týchto riešení v každom bode rovnice nenulový. interval (a, b).

Dôkaz. Predpokladajme opak. Existuje X0, kde W(X0)=0. Zostavíme sústavu n rovníc

(5).

Je zrejmé, že systém (5) má nenulové riešenie. Nechajte (6).

Zostavme lineárnu kombináciu riešení y1,…, yn.

Y(x) je riešením rovnice L[y] = 0. Okrem toho . Na základe vety o jedinečnosti môže byť riešenie rovnice L[y] = 0 s nulovými počiatočnými podmienkami iba nulové, t.j.

Dostaneme identitu , kde nie všetky sú rovné nule, čo znamená, že y1,…, yn sú lineárne závislé, čo je v rozpore s podmienkou vety. Preto neexistuje bod, kde by W(X0)=0.

Na základe vety 1 a vety 2 môžeme sformulovať nasledujúce tvrdenie. Aby bolo n riešení rovnice L[y] = 0 lineárne nezávislých v intervale (a, b), je potrebné a postačujúce, aby ich wronskián v žiadnom bode tohto intervalu nezanikol.

Z dokázaných teorémov vyplývajú aj nasledujúce zrejmé vlastnosti wronského.

1. Ak je Wronskián n riešení rovnice L[y] = 0 rovný nule v jednom bode x = x0 z intervalu (a, b), v ktorom sú všetky koeficienty pi(x) spojité, potom sa rovná nule. vo všetkých bodoch tohto intervalu.
2. Ak je Wronskián n riešení rovnice L[y] = 0 nenulový v jednom bode x = x0 z intervalu (a, b), potom je nenulový vo všetkých bodoch tohto intervalu.

Pre linearitu n nezávislých riešení rovnice L[y] = 0 v intervale (a, b), v ktorom sú koeficienty rovnice pi(x) spojité, je teda potrebné a postačujúce, aby ich wronskián bol nenulové aspoň v jednom bode tohto intervalu .

Lineárne (vektorové) priestory.

Definícia: Kopa L volal lineárny (vektorový) priestor , ak sú na ňom zavedené dve operácie:

1) prídavok: pre akékoľvek x, y Є L suma ( x + y) Є L,

2) násobenie číslom: pre ľubovoľné x Є L a ľubovoľné číslo λ súčin

λx Є L,

ktoré spĺňajú 8 axióm:

1) x + y = y + x, kde x, y Є L;

2) (x + y)+z = x+(y + z), kde x, y, z Є L;

3) existuje nulový prvok Ө taký, že Ө + x = x, kde x Є L;

4) pre akékoľvek x Є L existuje len jeden opačný prvok

(-X) také že x + (-x) \u003d Ө;

5) 1 x = x, kde x Є L;

6) α(βх) = (αβ)х, kde x Є L, a a p sú čísla;

7) α(x + y) = αx + αy, kde x, y Є L, α - číslo;

8) (α + β) x = αx + βx, kde x Є L, α a β sú čísla.

Komentujte: Prvky lineárneho (vektorového) priestoru sa nazývajú vektory .

Príklady:

Množina reálnych čísel je lineárny priestor.

Množiny všetkých vektorov v rovine a v priestore sú lineárnym priestorom.

Množina všetkých matíc rovnakej veľkosti je lineárny priestor.

V lineárnom priestore je daný systém vektorov a 1, a 2, a 3, ... a n Є L.

Definícia: Vektor α 1 a 1 + α 2 a 2 +…+ α n a n Є L, kde a i(i = 1,…,n) - čísla, volané lineárna kombinácia (LK) vektory a 1, a 2, a 3, ... a n.

Definícia: Lineárny priestorový vektorový systém a 1, a 2, a 3, ... a n Є L volal lineárne nezávislé (LNZ) ak lineárna kombinácia

α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n =0 vtedy a len vtedy, ak koeficienty

α 1 =α 2 =α 3 =…=α n =0.

Definícia: Vektorový systém a 1, a 2, a 3, ... a n Є L volal lineárne závislé (LZ) ak existuje množina čísel α 1, α 2 ,α 3 … α n, z ktorých nie všetky sú rovné 0, takže lineárna kombinácia α 1 a 1 + α 2 a 2 +…+ α n a n = 0.

Príklady:

Tieto dva vektory sa nazývajú kolineárne ak sú rovnobežné s tou istou priamkou alebo ležia na tej istej priamke.

1) Uvažujme dva nenulové, nekolineárne vektory v rovine. Uhlopriečka = 0 .

Lineárna kombinácia je rovná nule, existuje nenulový koeficient, preto sú dva kolineárne vektory v rovine lineárne závislé.

Veta 1. Nevyhnutná a postačujúca podmienka pre lineárnu závislosť.

Aby bol systém vektorov v lineárnom priestore lineárne závislý, je potrebné a postačujúce, aby niektorý vektor tohto systému bol lineárnou kombináciou všetkých ostatných.

Doc-in: Potreba ().

Daný systém LZ. Je potrebné dokázať, že jeden vektor je LC všetkých ostatných.

a 1, a 2, a 3, ... a n– LZ sústava vektorov, t.j. medzi α 1, α 2 ,α 3 … α n je nenulové číslo, takže LC α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n = 0.

Predpokladáme, že určiť, že koeficient α1 ≠ 0. Vydeľte obe strany poslednej rovnosti o α1 ≠ 0:

Z toho teda vyplýva 1- LC iných vektorov.

Potreba bola preukázaná.

Primeranosť ().

Nech je jeden vektor lineárnou kombináciou ostatných. Je potrebné dokázať, že systém vektorov LZ.

Nechať byť α n \u003d α 1 a 1 + α 2 a 2 + α 3 a 3 + ... + α n -1 a n -1.

α 1 a 1 + α 2 a 2 + α 3 a 3 + ... + α n -1 a n -1 - 1α n \u003d 0.

Keďže existuje nenulový koeficient, potom systém vektorov a 1, a 2, a 3, ... a n je lineárne závislý.

Veta 2. Systém obsahujúci nulový vektor je lineárne závislý.

Doc-in: Uvažujme systém vektorov obsahujúcich nulový vektor. a 1, a 2, a 3, ... a n,Ө, kde Ө je nulový vektor. Je zrejmé, že platí nasledujúca rovnosť 0 а 1 + 0 а 2 +0 а 3 +…+ 5 Ө = 0.

Existuje nenulový koeficient rovný 5 a lineárna kombinácia sa rovná 0, z toho vyplýva, že systém vektorov LZ.

Veta 3. Systém obsahujúci lineárne závislý subsystém bude tiež lineárne závislý.

Doc-in: Zvážte systém vektorov a 1, a 2, ..., k, a k+1 ... a n, kde a 1, a 2, ..., a k je lineárne závislý kus. α 1 a 1 + α 2 a 2 + ... + α k a k \u003d 0. Existuje iný koeficient ako nula.

Je zrejmé, že pri rovnakých koeficientoch je rovnosť

α 1 a 1 + α 2 a 2 +…+α k a k +…+0 a k+1 +…+ 0 α n = 0.

Z toho vyplýva, že systém vektorov LZ.

V tomto článku sa budeme venovať:

• čo sú kolineárne vektory;
• aké sú podmienky pre kolineárne vektory;
• aké sú vlastnosti kolineárnych vektorov;
• aká je lineárna závislosť kolineárnych vektorov.

Kolineárne vektory sú vektory, ktoré sú rovnobežné s rovnakou čiarou alebo ležia na tej istej čiare.

Príklad 1

Podmienky pre kolineárne vektory

Dva vektory sú kolineárne, ak je splnená niektorá z nasledujúcich podmienok:

• podmienka 1 . Vektory a a b sú kolineárne, ak existuje číslo λ také, že a = λ b ;
• stav 2 . Vektory a a b sú kolineárne s rovnakým pomerom súradníc:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• stav 3 . Vektory a a b sú kolineárne za predpokladu, že vektorový súčin a nulový vektor sú rovnaké:

a ∥ b ⇔ a, b = 0

Poznámka 1

Podmienka 2 nepoužiteľné, ak je jedna z vektorových súradníc nula.

Poznámka 2

Podmienka 3 použiteľné len pre tie vektory, ktoré sú dané v priestore.

Príklady úloh na štúdium kolinearity vektorov

Skúmame kolinearitu vektorov a \u003d (1; 3) a b \u003d (2; 1).

ako sa rozhodnúť?

V tomto prípade je potrebné použiť 2. podmienku kolinearity. Pre dané vektory to vyzerá takto:

Rovnosť je nesprávna. Z toho môžeme usúdiť, že vektory a a b sú nekolineárne.

Odpoveď : a | | b

Príklad 2

Aká hodnota m vektora a = (1 ; 2) a b = (- 1 ; m) je potrebná, aby vektory boli kolineárne?

ako sa rozhodnúť?

Pomocou druhej kolineárnej podmienky budú vektory kolineárne, ak sú ich súradnice proporcionálne:

To ukazuje, že m = -2.

odpoveď: m = -2.

Kritériá lineárnej závislosti a lineárnej nezávislosti sústav vektorov

Systém vektorov vo vektorovom priestore je lineárne závislý iba vtedy, ak jeden z vektorov systému možno vyjadriť v podmienkach zvyšku vektorov systému.

Dôkaz

Nech je sústava e 1 , e 2 , . . . , e n je lineárne závislá. Zapíšme si lineárnu kombináciu tohto systému rovnajúcu sa nulovému vektoru:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

v ktorých sa aspoň jeden z koeficientov kombinácie nerovná nule.

Nech a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Obidve strany rovnosti delíme nenulovým koeficientom:

a k - 1 (ak - 1 a 1) e1 + (ak - 1 a k) ek +. . . + (ak - 1 a n) e n = 0

Označiť:

Ak - 1 a m , kde m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

V tomto prípade:

p1e1+. . . + βk - 1 ek - 1 + β k + 1 ek + 1 +. . . + n e n = 0

alebo ek = (-p1)e1+. . . + (- p k - 1) ek - 1 + (- p k + 1) ek + 1 +. . . + (- β n) a n

Z toho vyplýva, že jeden z vektorov systému je vyjadrený v podmienkach všetkých ostatných vektorov systému. Čo bolo potrebné preukázať (p.t.d.).

Primeranosť

Nech je jeden z vektorov lineárne vyjadrený v podmienkach všetkých ostatných vektorov systému:

e k = y1e1+. . . + γ k - 1 ek - 1 + y k + 1 ek + 1 + . . . + γ n e n

Vektor e k prenesieme na pravú stranu tejto rovnosti:

0 = y1e1+. . . + γ k - 1 ek - 1 - ek + y k + 1 ek + 1 + . . . + γ n e n

Keďže koeficient vektora e k je rovný - 1 ≠ 0, dostaneme netriviálne zobrazenie nuly systémom vektorov e 1 , e 2 , . . . , e n , a to zase znamená, že daný systém vektorov je lineárne závislý. Čo bolo potrebné preukázať (p.t.d.).

Dôsledok:

• Systém vektorov je lineárne nezávislý, keď žiadny z jeho vektorov nemôže byť vyjadrený v podmienkach všetkých ostatných vektorov systému.
• Vektorový systém, ktorý obsahuje nulový vektor alebo dva rovnaké vektory, je lineárne závislý.

Vlastnosti lineárne závislých vektorov

1. Pre 2- a 3-rozmerné vektory je podmienka splnená: dva lineárne závislé vektory sú kolineárne. Dva kolineárne vektory sú lineárne závislé.
2. Pre 3-rozmerné vektory je podmienka splnená: tri lineárne závislé vektory sú koplanárne. (3 koplanárne vektory - lineárne závislé).
3. Pre n-rozmerné vektory je splnená podmienka: n + 1 vektorov je vždy lineárne závislých.

Príklady riešenia úloh pre lineárnu závislosť alebo lineárnu nezávislosť vektorov

Skontrolujme vektory a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 pre lineárnu nezávislosť.

rozhodnutie. Vektory sú lineárne závislé, pretože rozmer vektorov je menší ako počet vektorov.

Príklad 4

Skontrolujme vektory a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 pre lineárnu nezávislosť.

rozhodnutie. Nájdeme hodnoty koeficientov, pri ktorých sa lineárna kombinácia bude rovnať nulovému vektoru:

x 1 a + x 2 b + x 3 c 1 = 0

Vektorovú rovnicu napíšeme vo forme lineárnej:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Tento systém riešime Gaussovou metódou:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Od 2. riadku odčítame 1., od 3. - 1.:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Odčítajte 2. od prvého riadku, pridajte 2. k 3.:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Z riešenia vyplýva, že systém má veľa riešení. To znamená, že existuje nenulová kombinácia hodnôt takých čísel x 1 , x 2 , x 3, pre ktoré sa lineárna kombinácia a, b, c rovná nulovému vektoru. Preto vektory a , b , c sú lineárne závislé. ​​​​​​​

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Vektorový priestor. Príklady a najjednoduchšie vlastnosti vektorových priestorov Lineárna závislosť a nezávislosť sústavy vektorov Podstata a hodnosť konečnej sústavy vektorov.

Lineárny alebo vektorový priestor L(P) nad poľom P je neprázdna množina L, na ktorej sú zavedené operácie:

1. sčítanie, to znamená, že každej dvojici prvkov množiny je priradený prvok tej istej množiny, označený x + yϵL

2. násobenie skalárom (čiže prvkom poľa P), to znamená, že ľubovoľný prvok λ ϵ P a ľubovoľný prvok x ϵ L sú spojené s jedným prvkom z L(P), označeným λx ϵ L( P).

V tomto prípade sú na operáciu kladené tieto podmienky:

1. X+ r= y+ x, pre ľubovoľné x,y ϵ L.

2.X+ (y + z) = (x + y) + z, x, y, z ϵ L. (asociativita kontrakcie)

3. existuje taká θ ϵ L, ktoré X+ θ =x pre najmä žiadne x ϵ L (existencia neutrálneho prvku vzhľadom na sčítanie) nie je prázdne;

4. pre ľubovoľné x ϵ L existuje prvok -x ϵ L taký, že X+(-x)= θ (existencia opačného prvku vzhľadom na sčítanie).

5.(αβ)х=α(βх), (asociatívnosť násobenia skalárom)

6.1*x=x (jednotka: násobenie neutrálnym (násobením) prvkom poľa P zachováva vektor).

7.(α+ β)* x= a* x+ β*x, (distributivity násobenia vektorom vzhľadom na sčítanie skalárov);

8. α * (x + y) = α*x+ α *y, (distributivity násobenia skalárom vzhľadom na sčítanie vektora).

Prvky množiny L sa nazývajú vektory a prvky poľa P sa nazývajú skaláre. Vlastnosti 1-4 sa zhodujú s axiómami abelovskej skupiny.

Najjednoduchší svätci:

1. Vektorový priestor je abelovská grupa sčítaním.

2. Pre ľubovoľné x ϵ L je opačný prvok -x ϵ L jediný

3. 0*X=θ, pre akékoľvek x ϵ L

4. 1*(-x)=-x pre hocikoho x ϵ L

5.α * θ = θ ,pre akékoľvek αϵ L

Príklad VP yav-Xia m \ v maticách s reálnymi zložkami rovnakého rádu s prirodzenou definíciou operácií sčítania a násobenia. Matice na číslo látky

Lineárna závislosť \ (nie) systém vektorov (definície, vlastnosti)

Veta. (Nevyhnutná a postačujúca podmienka pre lineárnu závislosť sústavy vektorov.)

Systém vektorov vo vektorovom priestore je lineárne závislý práve vtedy, ak jeden z vektorov systému je lineárne vyjadrený v podmienkach ostatných vektorov tohto systému.

Dôkaz. Potreba. Nech je sústava e 1 ..e n lineárne závislá. Potom podľa definície predstavuje nulový vektor netriviálnym spôsobom, t.j. existuje netriviálna lineárna kombinácia tohto systému vektorov rovná nulovému vektoru:

α 1 e 1 +..+ α n e n =0, pričom aspoň jeden z koeficientov tejto lineárnej kombinácie sa nerovná nule. Nech α k ≠0 ,kϵ 1,2…n Vydelíme obe časti predchádzajúcej rovnosti týmto nenulovým koeficientom (t.j. vynásobíme α k -1 *(α 1 e 1 +..+ αa n e n) =0

Označme: α k -1 α m =β m kde mϵ 1,2…,k-1,k+1,..,n Potom β 1 e 1+ … +β 1 e n =0 t.j. jeden z vektorov systému je lineárne vyjadrený v podmienkach iných vektorov tohto systému atď.

Primeranosť. Nech je jeden z vektorov systému lineárne vyjadrený v podmienkach iných vektorov tohto systému: e k =γ 1 e 1+..+ γ n e n

Keďže koeficient vo vektore e k je rovný -1≠0, potom máme netriviálnu reprezentáciu nuly systémom vektorov e 1 ..e n, čo znamená, že tento systém vektorov je lineárne závislý atď.

Veta bola dokázaná.

Dôsledok.

1. Systém vektorov vo vektorovom priestore je lineárne nezávislý práve vtedy, ak žiadny z vektorov systému nie je lineárne vyjadrený v podmienkach iných vektorov tohto systému.

2. Systém vektorov obsahujúci nulový vektor alebo dva rovnaké vektory je lineárne závislý.

Dôsledok.

Systém pozostávajúci z jedného vektora je lineárne nezávislý práve vtedy, ak je tento vektor nenulový.

Báza je množina vektorov vo vektorovom priestore tak, že ľubovoľný vektor tohto priestoru môže byť jednoznačne reprezentovaný ako lineárna kombinácia vektorov z tejto množiny - bázové vektory.

Počet vektorov zahrnutých v akomkoľvek maximálnom lineárne nezávislom subsystéme daného systému vektorov sa nazýva hodnosť systémov.

Veta. Dajme dva systémy P- rozmerové vektory:

a 1 ,a 2,¼, a r (9)

b 1 ,b 2,¼, bs, (10)

nie nevyhnutne lineárne nezávislé a hodnost systému (9) sa rovná číslu k, poradie systému (10) je číslo l. Ak je prvý systém lineárne vyjadrený v zmysle druhého, potom k £ l. Ak tieto systémy sú ekvivalentné, potom k = l.

Počet prvkov (kardinalita) maximálnej lineárne nezávislej podmnožiny priestoru nezávisí od výberu tejto podmnožiny a nazýva sa hodnosť alebo dimenzia priestoru a samotná táto podmnožina sa nazýva základ