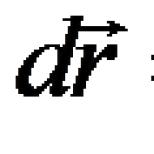Parciálne derivácie 3 premenných. Parciálne derivácie prvého rádu. úplný diferenciál. Podobne získame čiastočný prírastok z vzhľadom na y

Funkcie dvoch premenných, parciálne derivácie, diferenciály a gradient

Téma 5.Funkcie dvoch premenných.

parciálne deriváty

Definícia funkcie dvoch premenných, spôsoby nastavenia.

Súkromné deriváty.

Gradientová funkcia jednej premennej

Nájdenie najväčších a najmenších hodnôt funkcie dvoch premenných v uzavretej ohraničenej oblasti

1. Definícia funkcie viacerých premenných, spôsoby nastavenia

Pre funkcie dvoch premenných
doména definície je nejaký množina bodov na rovine
a rozsah je medzera na osi
.

Pre vizuálnu reprezentáciu funkcie dvoch premenných nyh aplikovať úrovňové čiary.

Príklad . Pre funkciu
zostavte graf a zarovnajte čiary. Napíšte rovnicu pre priamku prechádzajúcej bodom
.

Graf lineárnej funkcie je lietadlo vo vesmíre.

Pre funkciu je grafom rovina prechádzajúca bodmi
,
,
.

Riadky na úrovni funkcií sú rovnobežné priamky, ktorých rovnica
.

Pre lineárna funkcia dvoch premenných
úrovňové čiary sú dané rovnicou
a reprezentovať rodina rovnobežných čiar v rovine.

Graf funkcií 0 1 2 X

Riadky na úrovni funkcií

Súkromné proiderivačné funkcie dvoch premenných

Zvážte funkciu
. Dajme premennú v bode
ľubovoľný prírastok
, opúšťať premenlivá hodnota nezmenené. Zodpovedajúci prírastok funkcie

volal čiastočný prírastok funkcie premennou v bode
.

Podobne definované čiastočný prírastok funkciepodľa premennej: .

Označeniečiastočná derivácia vzhľadom na: , ,
,
.

Parciálna derivácia funkcie vzhľadom na premennú nazývaný limit :

Označenia: , ,
,
.

Na nájdenie parciálnej derivácie
v súvislosti s premennou sa používajú pravidlá pre diferenciáciu funkcie jednej premennej, za predpokladu, že premenná je konštantná.

Podobne nájsť parciálnu deriváciu vzhľadom na premennú premenná sa považuje za konštantnú .

Príklad . Pre funkciu
nájsť parciálne derivácie
,
a vypočítajte ich hodnoty v bode
.

Parciálna derivácia funkcie
premennou je za predpokladu, že je konštantná:

Nájdite čiastočnú deriváciu funkcie vzhľadom na , za predpokladu, že je konštantná:

Vypočítajme hodnoty parciálnych derivácií pre
,
:

;
.

Parciálne derivácie druhého rádu funkcie viacerých premenných sa nazývajú parciálne derivácie parciálnych derivácií prvého rádu.

Napíšme parciálne derivácie 2. rádu pre funkciu:

;
;

;
.

;
atď.

Ak sú zmiešané parciálne derivácie funkcie viacerých premenných v určitom bode spojité
, potom oni navzájom rovnocenné v tomto bode. Pre funkciu dvoch premenných teda hodnoty zmiešaných parciálnych derivácií nezávisia od poradia diferenciácie:

Príklad. Pre funkciu nájdite parciálne derivácie druhého rádu
a
.

rozhodnutie

Zmiešaná parciálna derivácia sa nájde postupným derivovaním prvej funkcie vzhľadom na (za predpokladu konštanty), potom diferenciácia derivácie
podľa (za predpokladu konštanty).

Derivácia sa nachádza tak, že sa najskôr derivuje funkcia vzhľadom na , potom derivácia vzhľadom na .

Zmiešané parciálne deriváty sú si navzájom rovné:
.

3. Gradient funkcie dvoch premenných

gradientové vlastnosti

Príklad . Daná funkcia
. Nájdite prechod
v bode
a postaviť ho.

rozhodnutie

Nájdite súradnice gradientu - parciálne derivácie.

V bode
gradient rovná sa . Vektorový štart
v bode a koniec v bode .

4. Nájdenie najväčšej a najmenšej hodnoty funkcie dvoch premenných v uzavretej ohraničenej oblasti

Formulácia problému. Nechajte na rovine uzavretú ohraničenú oblasť
je daná sústavou nerovností tvaru
. Je potrebné nájsť body v oblasti, v ktorej funkcia nadobúda najväčšie a najmenšie hodnoty.

Dôležité je extrémny problém, ktorej matematický model obsahuje lineárne obmedzenia (rovnice, nerovnosti) a lineárne funkciu
.

Formulácia problému. Nájdite najväčšiu a najmenšiu hodnotu funkcie
(2.1)

pod obmedzeniami

(2.2)

. (2.3)

Pretože neexistujú žiadne kritické body pre lineárnu funkciu mnohých premenných vnútri oblasti
, potom sa dosiahne len optimálne riešenie, ktoré poskytuje cieľovú funkciu s extrémom na okraji regiónu. Pre oblasť definovanú lineárnymi obmedzeniami sú možné extrémne body rohové body. To nám umožňuje zvážiť riešenie problému grafická metóda.

Grafické riešenie sústavy lineárnych nerovníc

Pre grafické riešenie tohto problému je potrebné vedieť graficky riešiť sústavy lineárnych nerovníc s dvoma premennými.

Postup:

Všimnite si, že nerovnosť
definuje pravá súradnicová polrovina(od osi
) a nerovnosť
- horná súradnicová polrovina(od osi
).

Príklad. Vyriešte graficky nerovnosť
.

Napíšeme rovnicu hraničnej čiary
a zostaviť ho z dvoch bodov, napr.
a
. Priamka rozdeľuje rovinu na dve polroviny.

Súradnice bodu
uspokojiť nerovnosť (
je pravda), čo znamená, že súradnice všetkých bodov polroviny obsahujúcej bod vyhovujú nerovnosti. Riešením nerovnosti budú súradnice bodov polroviny nachádzajúcich sa vpravo od hraničnej čiary vrátane bodov na hranici. Požadovaná polrovina je na obrázku zvýraznená.

rozhodnutie
systém nerovností je tzv prípustné, ak sú jeho súradnice nezáporné , . Súbor prípustných riešení sústavy nerovností tvorí oblasť, ktorá sa nachádza v prvej štvrtine súradnicovej roviny.

Príklad. Zostrojte oblasť riešenia sústavy nerovností

Riešenia nerovností sú:

1)
- polrovina umiestnená vľavo a nižšie vzhľadom na priamku ( )
;

2)
je polrovina umiestnená v pravej dolnej polrovine vzhľadom na priamku ( )
;

3)
- polrovina umiestnená napravo od priamky ( )
;

4) - polrovina nad osou x, to znamená priamka ( )
.

Oblasť prípustných riešení daný systém lineárnych nerovností je množina bodov nachádzajúcich sa vo vnútri a na hranici štvoruholníka
, ktorý je križovatkaštyri polovičné roviny.

Geometrická reprezentácia lineárnej funkcie

(úrovňové čiary a gradient)

Opravme hodnotu
, dostaneme rovnicu
, ktorý geometricky vymedzuje priamku. V každom bode nadobúda priama funkcia hodnotu a je nivelačná čiara. dávať rôzne hodnoty, napr.

, ... , dostaneme množinu čiar úrovne - sada paralelných priamy.

Poďme stavať gradient- vektor
, ktorých súradnice sa rovnajú hodnotám koeficientov premenných vo funkcii
. Tento vektor je: 1) kolmý na každú priamku (úrovňová čiara)
; 2) ukazuje smer nárastu účelovej funkcie.

Príklad . Nakreslite čiary úrovne a prechod prvkov
.

Čiary úrovne na , , sú rovné

,
,

, navzájom paralelné. Gradient je vektor kolmý na každú čiaru úrovne.

Grafické zistenie najväčších a najmenších hodnôt lineárnej funkcie v regióne

Geometrické vyjadrenie problému. Nájdite v doméne riešenia sústavy lineárnych nerovníc bod, ktorým prechádza čiara úrovne, zodpovedajúci najväčšej (najmenšej) hodnote lineárnej funkcie s dvoma premennými.

Sekvenovanie:

4. Nájdite súradnice bodu A riešením sústavy rovníc priamok pretínajúcich sa v bode A a vypočítajte najmenšiu hodnotu funkcie
. Podobne - pre bod B a najväčšiu hodnotu funkcie
. postavené na bodoch.premenné Súkromnéderivátyfunkcie niekoľko premenné a diferenciačnej techniky. Extrémne funkciedvapremenné a jeho nevyhnutné...

Každá čiastočná derivácia (nad X a podľa r) funkcie dvoch premenných je obyčajná derivácia funkcie jednej premennej s pevnou hodnotou druhej premennej:

(kde r= konštanta),

(kde X= konštanta).

Preto sa parciálne deriváty počítajú z vzorce a pravidlá na výpočet derivácií funkcií jednej premennej, pričom druhú premennú považujeme za konštantu (konštantu).

Ak nepotrebujete analýzu príkladov a na to potrebnú minimálnu teóriu, ale potrebujete len riešenie svojho problému, pokračujte online kalkulačka parciálnych derivácií .

Ak je ťažké zamerať sa na sledovanie toho, kde je konštanta vo funkcii, potom môžete nahradiť akékoľvek číslo v návrhu riešenia príkladu namiesto premennej pevnou hodnotou - potom môžete rýchlo vypočítať parciálnu deriváciu ako obyčajnú derivácia funkcie jednej premennej. Len je potrebné nezabudnúť pri dokončovaní vrátiť konštantu (premennú s pevnou hodnotou) na jej miesto.

Vyššie opísaná vlastnosť parciálnych derivácií vyplýva z definície parciálnej derivácie, ktorú možno nájsť v skúšobných otázkach. Preto, aby ste sa zoznámili s definíciou uvedenou nižšie, môžete otvoriť teoretickú referenciu.

Koncept spojitosti funkcie z= f(X, r) v bode je definovaný podobne ako tento pojem pre funkciu jednej premennej.

Funkcia z = f(X, r) sa nazýva spojitý v bode, ak

Rozdiel (2) sa nazýva celkový prírastok funkcie z(získa sa zvýšením oboch argumentov).

Nechajte funkciu z= f(X, r) a bodka

Ak sa funkcia zmení z nastane, keď sa zmení iba jeden z argumentov, napr. X s pevnou hodnotou druhého argumentu r, potom sa funkcia zvýši

nazývaný čiastočný prírastok funkcie f(X, r) zapnuté X.

Vzhľadom na zmenu funkcie z v závislosti od zmeny len jedného z argumentov vlastne prechádzame na funkciu jednej premennej.

Ak existuje konečný limit

potom sa nazýva parciálna derivácia funkcie f(X, r) argumentom X a je označený jedným zo symbolov

(4)

Čiastočný prírastok je definovaný podobne z na r:

a čiastočná derivácia f(X, r) zapnuté r:

(6)

Príklad 1

rozhodnutie. Nájdeme parciálnu deriváciu vzhľadom na premennú "x":

(r pevné);

Nájdeme parciálnu deriváciu vzhľadom na premennú "y":

(X pevné).

Ako vidíte, nezáleží na tom, do akej miery je premenná pevná: v tomto prípade je to len nejaké číslo, ktoré je súčiniteľom (ako v prípade obvyklej derivácie) s premennou, pomocou ktorej nájdeme čiastočnú derivát. Ak sa pevná premenná nevynásobí premennou, vzhľadom na ktorú nájdeme parciálnu deriváciu, potom táto osamelá konštanta, bez ohľadu na to, do akej miery, ako v prípade obyčajnej derivácie, zaniká.

Príklad 2 Daná funkcia

Nájdite čiastočné deriváty

(x) a (by y) a vypočítajte ich hodnoty v bode ALE (1; 2).

rozhodnutie. Pri pevnom r derivácia prvého člena sa nachádza ako derivácia mocninovej funkcie ( tabuľka derivačných funkcií jednej premennej):

Pri pevnom X derivácia prvého člena sa nachádza ako derivácia exponenciálnej funkcie a druhá - ako derivácia konštanty:

Teraz vypočítame hodnoty týchto parciálnych derivácií v bode ALE (1; 2):

Riešenie úloh s parciálnymi deriváciami si môžete skontrolovať na online kalkulačka parciálnych derivácií .

Príklad 3 Nájdite čiastočné deriváty funkcií

rozhodnutie. V jednom kroku nájdeme

(r X, ako keby argument sínus bol 5 X: rovnakým spôsobom sa pred znakom funkcie objaví 5);

(X je pevná a je v tomto prípade faktorom r).

Riešenie úloh s parciálnymi deriváciami si môžete skontrolovať na online kalkulačka parciálnych derivácií .

Parciálne derivácie funkcie troch alebo viacerých premenných sú definované podobne.

Ak každá sada hodnôt ( X; r; ...; t) nezávislé premenné z množiny D zodpovedá jednej konkrétnej hodnote u od mnohých E, potom u sa nazýva funkcia premenných X, r, ..., t a označujú u= f(X, r, ..., t).

Pre funkcie troch alebo viacerých premenných neexistuje žiadna geometrická interpretácia.

Parciálne derivácie funkcie viacerých premenných sú tiež definované a vypočítané za predpokladu, že sa mení iba jedna z nezávislých premenných, zatiaľ čo ostatné sú pevné.

Príklad 4 Nájdite čiastočné deriváty funkcií

rozhodnutie. r a z opravené:

X a z opravené:

X a r opravené:

Nájdite parciálne deriváty sami a potom si pozrite riešenia

Príklad 5

Príklad 6 Nájdite parciálne derivácie funkcie.

Parciálna derivácia funkcie viacerých premenných má to isté mechanický význam ako derivácia funkcie jednej premennej, je rýchlosť, ktorou sa funkcia mení vzhľadom na zmenu jedného z argumentov.

Príklad 8 prietokové množstvo P cestujúcich na železnici možno vyjadriť ako funkciu

kde P- počet cestujúcich, N- počet obyvateľov príslušných bodov, R- vzdialenosť medzi bodmi.

Parciálna derivácia funkcie P na R rovná

ukazuje, že pokles toku cestujúcich je nepriamo úmerný druhej mocnine vzdialenosti medzi zodpovedajúcimi bodmi pre rovnaký počet obyvateľov v bodoch.

Čiastočná derivácia P na N rovná

ukazuje, že nárast toku cestujúcich je úmerný dvojnásobnému počtu obyvateľov sídiel s rovnakou vzdialenosťou medzi bodmi.

Riešenie úloh s parciálnymi deriváciami si môžete skontrolovať na online kalkulačka parciálnych derivácií .

Úplný diferenciál

Súčin parciálnej derivácie a prírastku príslušnej nezávislej premennej sa nazýva parciálny diferenciál. Čiastočné rozdiely sú označené takto:

Súčet parciálnych diferenciálov nad všetkými nezávislými premennými dáva celkový diferenciál. Pre funkciu dvoch nezávislých premenných je celkový diferenciál vyjadrený rovnosťou

(7)

Príklad 9 Nájdite úplný diferenciál funkcie

rozhodnutie. Výsledok použitia vzorca (7):

Funkcia, ktorá má totálny diferenciál v každom bode určitej oblasti, sa v tejto oblasti nazýva diferencovateľná.

Nájdite celkový rozdiel sami a potom si pozrite riešenie

Rovnako ako v prípade funkcie jednej premennej, diferencovateľnosť funkcie v určitom regióne implikuje jej kontinuitu v tomto regióne, ale nie naopak.

Formulujme bez dôkazu dostatočnú podmienku diferencovateľnosti funkcie.

Veta. Ak je funkcia z= f(X, r) má spojité parciálne derivácie

v danom regióne, potom je v tomto regióne diferencovateľný a jeho diferenciál je vyjadrený vzorcom (7).

Dá sa ukázať, že tak ako v prípade funkcie jednej premennej je diferenciál funkcie hlavnou lineárnou časťou prírastku funkcie, tak aj v prípade funkcie viacerých premenných je celkový diferenciál hlavná, lineárna vzhľadom na prírastky nezávisle premenných, časť celkového prírastku funkcie.

Pre funkciu dvoch premenných má celkový prírastok funkcie tvar

(8)

kde α a β sú nekonečne malé pre a .

Parciálne deriváty vyšších rádov

Parciálne derivácie a funkcie f(X, r) sú samy osebe niektorými funkciami tých istých premenných a naopak môžu mať derivácie vzhľadom na rôzne premenné, ktoré sa nazývajú parciálne derivácie vyšších rádov.

Definícia 1.11 Nech je daná funkcia dvoch premenných z=z(x,y), (x,y)D . Bodka M 0 (X 0 ;y 0 ) - vnútorný bod oblasti D .

Ak v D existuje taká štvrť UM 0 bodov M 0 , čo pre všetky body

potom bod M 0 sa nazýva lokálny maximálny bod. Ale samotný význam z(M 0 ) - miestne maximum.

Ale ak za všetky body

potom bod M 0 sa nazýva lokálny minimálny bod funkcie z(x,y) . Ale samotný význam z(M 0 ) - miestne minimum.

Lokálne maximum a lokálne minimum sa nazývajú lokálne extrémy funkcie z(x,y) . Na obr. 1.4 vysvetľuje geometrický význam lokálneho maxima: M 0 je maximálny bod, keďže na povrchu z=z(x,y) jej zodpovedajúci bod C 0 je nad akýmkoľvek susedným bodom C (toto je lokalita maxima).

Všimnite si, že na povrchu sú body ako celok (napr. AT ), ktoré sú vyššie C 0 , ale tieto body (napr. AT ) nie sú „susedné“ s bodom C 0 .

Najmä pointa AT zodpovedá konceptu globálneho maxima:

Globálne minimum je definované podobne:

Hľadanie globálnych maxím a miním bude diskutované v časti 1.10.

Veta 1.3(nevyhnutné extrémne podmienky).

Nechajte funkciu z =z(x,y),(x,y)D . Bodka M 0 (X 0 ;y 0 D - lokálny extrémny bod.

Ak v tomto bode existujú z" X a z" r , potom

Geometrický dôkaz je "zrejmý". Ak v bode C 0 na (obr. 1.4) nakresliť dotykovú rovinu, potom bude „prirodzene“ prechádzať vodorovne, t.j. 0° do osi Oh a na os OU .

Potom v súlade s geometrickým významom parciálnych derivácií (obr. 1.3):

čo sa malo dokázať.

Definícia 1.12.

Ak v bode M 0 sú splnené podmienky (1.41), potom sa nazýva stacionárny bod funkcie z (x,y) .

Veta 1.4(dostatočné podmienky pre extrém).

Nechaj z =z(x,y),(x,y)D , ktorý má v niektorom okolí bodu parciálne derivácie druhého rádu M 0 (X 0 ,y 0 )D . A M 0 - stacionárny bod (t. j. potrebné podmienky (1.41) sú splnené). Poďme počítať:

Dôkaz vety využíva témy (Taylorov vzorec pre funkcie viacerých premenných a teória kvadratických foriem), ktoré nie sú zahrnuté v tomto návode.

Príklad 1.13.

Preskúmajte extrémy:

rozhodnutie

1. Nájdite stacionárne body riešením systému (1.41):

to znamená, že sa nájdu štyri stacionárne body. 2.

podľa vety 1.4 v bode je minimum. A

podľa vety 1.4 v bode

Maximálne. A

A nemusíte nič hľadať: v našom samostatnom článku sme už všetko pripravili, aby ste to mohli urobiť. Teraz hovorme o parciálnych deriváciách.

Vitajte na našom telegramovom kanáli, kde nájdete užitočné bulletiny a aktuálne študentské správy.

Funkcia dvoch alebo viacerých premenných

Predtým, ako hovoríme o parciálnych deriváciách, musíme sa dotknúť konceptu funkcie viacerých premenných, bez ktorej parciálna derivácia nemá zmysel. V škole sme zvyknutí narábať s funkciami jednej premennej:

Predtým sme uvažovali o derivátoch takýchto funkcií. Grafom funkcie jednej premennej je priamka v rovine: priamka, parabola, hyperbola atď.

Čo ak pridáme ďalšiu premennú? Získate funkciu ako je táto:

Ide o funkciu dvoch nezávislých premenných X a r. Grafom takejto funkcie je plocha v trojrozmernom priestore: guľa, hyperboloid, paraboloid alebo nejaký iný sférický kôň vo vákuu. Parciálne derivačné funkcie z pre x a y sa píšu takto:

Existujú aj funkcie troch alebo viacerých premenných. Je pravda, že nie je možné nakresliť graf takejto funkcie: vyžadovalo by si to aspoň štvorrozmerný priestor, ktorý nemožno zobraziť.

Čiastočná derivácia prvého rádu

Pamätajte na hlavné pravidlo:

Pri výpočte parciálnej derivácie vzhľadom na jednu z premenných sa druhá premenná berie ako konštanta. V opačnom prípade sa pravidlá pre výpočet derivátu nemenia.

To znamená, že čiastočná derivácia sa v podstate nelíši od bežnej. Majte teda pred očami tabuľku derivácií elementárnych funkcií a pravidlá na výpočet obyčajných derivácií. Pozrime sa na príklad, aby to bolo celkom jasné. Povedzme, že chcete vypočítať parciálne derivácie prvého rádu nasledujúcej funkcie:

Najprv vezmeme parciálnu deriváciu vzhľadom na x, pričom y považujeme za obyčajné číslo:

Teraz uvažujeme parciálnu deriváciu vzhľadom na y, pričom x berieme ako konštantu:

Ako vidíte, nie je na tom nič zložité a úspech so zložitejšími príkladmi je len vecou cviku.

Čiastočná derivácia druhého rádu

Čo je parciálna derivácia druhého rádu? Rovnako ako ten prvý. Ak chcete nájsť parciálne derivácie druhého rádu, stačí vziať deriváciu z derivácie prvého rádu. Vráťme sa k vyššie uvedenému príkladu a vypočítajme parciálne derivácie druhého rádu.

Podľa hry:

Parciálne deriváty tretieho a vyššieho rádu sa v princípe výpočtu nelíšia. Poďme usporiadať pravidlá:

Pri diferenciácii vzhľadom na jednu nezávislú premennú sa druhá berie ako konštanta.
Derivát druhého rádu je derivátom prvého rádu. Tretí rád je derivát druhého rádu atď.

Parciálne derivácie a totálny diferenciál funkcie

Častou otázkou v praktických úlohách je hľadanie totálneho diferenciálu funkcie. Pre funkciu niekoľkých premenných je celkový diferenciál definovaný ako hlavná lineárna časť malého celkového prírastku funkcie vzhľadom na prírastky argumentov.

Definícia znie ťažkopádne, no s písmenami je všetko jednoduchšie. Celkový diferenciál prvého rádu funkcie niekoľkých premenných vyzerá takto:

Keďže vieme, ako sa počítajú parciálne derivácie, nie je problém vypočítať celkový diferenciál.

Parciálne deriváty nie sú až taká zbytočná téma. Napríklad parciálne diferenciálne rovnice druhého rádu sa široko používajú na matematický popis reálnych fyzikálnych procesov.

Tu sme uviedli iba všeobecnú, povrchnú predstavu o čiastočných derivátoch prvého a druhého rádu. Zaujíma vás táto téma alebo máte konkrétne otázky? Opýtajte sa ich v komentároch a obráťte sa na odborníkov profesionálneho študentského servisu pre kvalifikovanú a rýchlu pomoc pri štúdiu. S nami nezostanete s problémom sami!

Všeobecný princíp hľadania parciálnych derivácií druhého rádu funkcie troch premenných je podobný princípu hľadania parciálnych derivácií druhého rádu funkcie dvoch premenných.

Aby ste našli parciálne derivácie druhého rádu, musíte najprv nájsť parciálne derivácie prvého rádu alebo v inom zápise:

Existuje deväť parciálnych derivátov druhého rádu.

Prvou skupinou sú druhé deriváty vzhľadom na rovnaké premenné:

Alebo - druhá derivácia vzhľadom na "x";

Alebo - druhá derivácia vzhľadom na "y";

Alebo - druhá derivácia vzhľadom na "z".

Druhá skupina je zmiešanéčiastočné deriváty 2. rádu, je ich šesť:

alebo - zmiešané derivácia "podľa x y";

alebo - zmiešané derivácia "by y x";

alebo - zmiešané derivát "by x z";

alebo - zmiešané derivát "po zet x";

alebo - zmiešané derivácia "podľa hry z";

alebo - zmiešané derivát "po z y".

Rovnako ako v prípade funkcie dvoch premenných sa pri riešení úloh možno zamerať na nasledujúce rovnosti zmiešaných derivácií druhého rádu:

Poznámka: Presne povedané, nie je to vždy tak. Pre rovnosť zmiešaných derivátov je potrebné splniť požiadavku ich kontinuity.

Pre každý prípad niekoľko príkladov, ako túto hanbu prečítať nahlas:

- "dva ťahy dvakrát za y";

- „de two y po de zet square“;

- „dva ťahy na x na z“;

- „de dva y po de z po de y“.

Príklad 10

Nájdite všetky parciálne derivácie prvého a druhého rádu pre funkciu troch premenných:

rozhodnutie: Najprv nájdeme parciálne derivácie prvého rádu:

Vezmeme nájdený derivát

a odlíšiť ho "y":

Vezmeme nájdený derivát

a odlíšiť ho "x":

Rovnosť je hotová. Dobre.

Zaoberáme sa druhou dvojicou zmiešaných derivátov.

Vezmeme nájdený derivát

a odlíšiť ho "z":

Vezmeme nájdený derivát

a odlíšiť ho "x":

Rovnosť je hotová. Dobre.

Podobne sa zaoberáme treťou dvojicou zmiešaných derivátov:

Rovnosť je hotová. Dobre.

Po vykonanej práci je možné zaručiť, že po prvé sme správne našli všetky parciálne derivácie 1. rádu a po druhé, správne sme našli aj zmiešané parciálne derivácie 2. rádu.

Zostáva nájsť tri ďalšie parciálne deriváty druhého rádu, tu by ste sa mali čo najviac sústrediť, aby ste sa vyhli chybám:

Pripravený. Opäť platí, že úloha nie je ani tak náročná ako objemná. Riešenie je možné skrátiť a označiť ako rovnosti zmiešaných parciálnych derivácií, ale v tomto prípade nedôjde k overeniu. Preto je lepšie nájsť si čas všetky deriváty (okrem toho to môže vyžadovať učiteľ), alebo v krajnom prípade skontrolovať návrh.

Príklad 11

Nájdite všetky parciálne derivácie prvého a druhého rádu pre funkciu troch premenných

Toto je príklad „urob si sám“.

Riešenia a odpovede:

Príklad 2:rozhodnutie:

Príklad 4:rozhodnutie: Nájdite parciálne derivácie prvého rádu.

Zložíme celkový diferenciál prvého rádu:

Príklad 6:rozhodnutie: M(1, -1, 0):

Príklad 7:rozhodnutie: Vypočítajme parciálne derivácie prvého rádu v bodeM(1, 1, 1):

Príklad 9:rozhodnutie:

Príklad 11:rozhodnutie: Nájdite parciálne derivácie prvého rádu:

Nájdite parciálne derivácie druhého rádu:

Integrály

8.1. Neurčitý integrál. Podrobné príklady riešení

Začnime študovať tému Neurčitý integrál" a tiež podrobne analyzovať príklady riešení najjednoduchších (a nie celkom) integrálov. Ako obvykle, obmedzíme sa na minimálnu teóriu, ktorá je v početných učebniciach, našou úlohou je naučiť sa riešiť integrály.

Čo potrebujete vedieť, aby ste látku úspešne zvládli? Aby ste sa vyrovnali s integrálnym počtom, musíte byť schopní nájsť deriváty, aspoň na priemernej úrovni. Nebude to zbytočná skúsenosť, ak máte za sebou niekoľko desiatok alebo lepšie sto samostatne nájdených derivátov. Prinajmenšom by ste sa nemali nechať zmiasť úlohou odlíšiť najjednoduchšie a najbežnejšie funkcie.

Zdalo by sa, kde sú vôbec derivácie, ak sa v článku bavíme o integráloch?! A tu je tá vec. Faktom je, že hľadanie derivátov a hľadanie neurčitých integrálov (diferenciácia a integrácia) sú dve vzájomne inverzné akcie, ako je sčítanie / odčítanie alebo násobenie / delenie. Bez zručnosti a akej-takej skúsenosti s hľadaním derivátov sa teda, žiaľ, nedá ďalej napredovať.

V tejto súvislosti budeme potrebovať nasledujúce metodické materiály: Tabuľka derivátov a Tabuľka integrálov.

Aké sú ťažkosti pri štúdiu neurčitých integrálov? Ak v derivátoch existuje striktne 5 pravidiel diferenciácie, tabuľka derivátov a pomerne jasný algoritmus akcií, potom v integráloch je všetko iné. Existujú desiatky integračných metód a techník. A ak bola metóda integrácie pôvodne zvolená nesprávne (to znamená, že neviete, ako ju vyriešiť), integrál môže byť doslova „pichnutý“ doslova celé dni, ako skutočný rébus, snažiac sa všimnúť si rôzne triky a triky. . Niektorým sa to dokonca páči.

Mimochodom, pomerne často sme od študentov (nie humanitných vied) počúvali názor typu: „Nikdy som nemal záujem riešiť limitu alebo deriváciu, ale integrály sú úplne iná záležitosť, je to vzrušujúce, vždy je tu chuť „ crack „komplexný integrál“. Stop. Dosť bolo čierneho humoru, prejdime k týmto veľmi neurčitým integrálom.

Keďže existuje veľa spôsobov riešenia, kde potom čajník začne študovať neurčité integrály? V integrálnom počte sú podľa nás tri piliere alebo akási „os“, okolo ktorej sa točí všetko ostatné. V prvom rade by ste mali dobre rozumieť najjednoduchším integrálom (tento článok).

Potom musíte lekciu podrobne vypracovať. TOTO JE NAJDÔLEŽITEJŠIA RECEPCIA! Možno dokonca najdôležitejší článok zo všetkých článkov venovaných integrálom. A do tretice si určite prečítajte integrácia po častiach, pretože integruje širokú triedu funkcií. Ak ovládate aspoň tieto tri lekcie, potom už „nie sú dve“. Môže vám byť odpustené, že to neviete integrály goniometrických funkcií, integrály zlomkov, integrály zlomkových racionálnych funkcií, integrály iracionálnych funkcií (odmocniny), ale ak sa „dostanete do kaluže“ pri metóde výmeny alebo metóde integrácie dielov, bude to veľmi, veľmi zlé.

Začnime teda jednoducho. Pozrime sa na tabuľku integrálov. Podobne ako pri deriváciách si všimneme niekoľko integračných pravidiel a tabuľku integrálov niektorých elementárnych funkcií. Akýkoľvek tabuľkový integrál (a vlastne každý neurčitý integrál) má tvar:

Poďme rovno k notácii a pojmom:

- integrálna ikona.

- integrandová funkcia (písaná písmenom "s").

– ikona rozdielu. Čo to je, zvážime veľmi skoro. Hlavná vec je, že pri písaní integrálu a počas riešenia je dôležité nestratiť túto ikonu. Bude tam viditeľná chyba.

je integrand alebo "výplň" integrálu.

– primitívny funkciu.

– . Netreba sa zaťažovať pojmami, tu je najdôležitejšie, že v akomkoľvek neurčitom integráli sa k odpovedi pridáva konštanta.

Vyriešiť neurčitý integrál znamená nájsťsúbor primitívnych funkcií z daného integrandu

Pozrime sa ešte raz na záznam:

Pozrime sa na tabuľku integrálov.

Čo sa deje? Naše ľavé časti sa otáčajú na ďalšie funkcie: .

Zjednodušme si definíciu:

Vyriešte neurčitý integrál - to znamená PREMENIŤ ho na neurčitú (až konštantnú) funkciu pomocou niektorých pravidiel, techník a tabuľky.

Vezmime si napríklad tabuľkový integrál . Čo sa stalo? Symbolický záznam sa zmenil na súbor primitívnych funkcií.

Podobne ako v prípade derivácií, na to, aby sme sa naučili nájsť integrály, nie je potrebné vedieť, čo je to integrál alebo primitívna funkcia z teoretického hľadiska. Stačí vykonať transformácie podľa niektorých formálnych pravidiel. Takže v prípade nie je vôbec potrebné chápať, prečo sa integrál mení na presne. Tento a ďalšie vzorce môžete považovať za samozrejmosť. Každý používa elektrinu, ale len málo ľudí premýšľa o tom, ako elektróny prebiehajú pozdĺž drôtov.

Keďže diferenciácia a integrácia sú opačné operácie, pre každý primitívny prvok, ktorý sa nájde správne, platí toto:

Inými slovami, ak je správna odpoveď diferencovaná, potom je potrebné získať pôvodný integrand.

Vráťme sa k rovnakému tabuľkovému integrálu .

Overme si platnosť tohto vzorca. Zoberieme deriváciu pravej strany:

je pôvodný integrand.

Mimochodom, bolo jasnejšie, prečo je konštanta vždy priradená k funkcii. Pri diferenciácii sa konštanta vždy zmení na nulu.

Vyriešte neurčitý integrál znamená nájsť kopa všetky primitívne deriváty a nie nejakú samostatnú funkciu. V uvažovanom tabuľkovom príklade , , , atď. - všetky tieto funkcie sú riešením integrálu . Riešení je nekonečne veľa, preto píšu stručne:

Akýkoľvek neurčitý integrál je teda dostatočne jednoduchý na kontrolu. Toto je určitá kompenzácia veľkého počtu integrálov rôznych typov.

Prejdime na konkrétne príklady. Začnime, ako pri štúdiu derivátu, dvoma pravidlami integrácie:

- stály C môže (a malo by) byť vyňaté z integrálneho znamienka.

– integrál súčtu (rozdielu) dvoch funkcií sa rovná súčtu (rozdielu) dvoch integrálov. Toto pravidlo platí pre ľubovoľný počet termínov.

Ako vidíte, pravidlá sú v podstate rovnaké ako pre deriváty. Niekedy sú tzv vlastnosti linearity integrálne.

Príklad 1

Nájdite neurčitý integrál.

Spustite kontrolu.

rozhodnutie: Je pohodlnejšie previesť to ako.

(1) Uplatnenie pravidla . Nezabudnite si zapísať ikonu rozdielu dx pod každým integrálom. Prečo pod každým? dxje plný multiplikátor. Ak maľujete podrobne, potom by mal byť prvý krok napísaný takto:

(2) Podľa pravidla vyberieme všetky konštanty zo znamienok integrálov. Všimnite si, že v poslednom termíne tg 5 je konštanta, tiež ju vytiahneme.

Okrem toho v tomto kroku pripravujeme korene a stupne integrácie. Rovnako ako pri diferenciácii musia byť korene zastúpené vo forme . Korene a stupne, ktoré sa nachádzajú v menovateli - pohyb nahor.

Poznámka: na rozdiel od derivácií, korene v integráloch nemusia byť vždy redukované do tvaru a posuňte stupne nahor.

Napríklad, - toto je hotový tabuľkový integrál, ktorý už bol vypočítaný pred vami, a všetky druhy čínskych trikov ako úplne zbytočné. Podobne: - toto je tiež tabuľkový integrál, nemá zmysel uvádzať zlomok v tvare . Pozorne si preštudujte tabuľku!

(3) Všetky integrály sú tabuľkové. Transformáciu vykonáme pomocou tabuľky pomocou vzorcov: a

pre funkciu napájania - .

Treba poznamenať, že tabuľkový integrál je špeciálnym prípadom vzorca pre výkonovú funkciu: .

Neustále C stačí ho pridať raz na koniec výrazu

(namiesto toho, aby ste ich dávali za každým integrálom).

(4) Získaný výsledok zapisujeme v kompaktnejšom tvare, keď sú všetky stupne tvaru

opäť reprezentujú ako odmocniny a mocniny so záporným exponentom sa vrátia späť na menovateľa.

Vyšetrenie. Ak chcete vykonať kontrolu, musíte rozlíšiť prijatú odpoveď:

Počiatočné integrand, teda integrál bol nájdený správne. Od toho, čo tancovali, sa k tomu vrátili. Je dobré, keď sa príbeh s integrálom skončí len tak.

Z času na čas existuje trochu iný prístup ku kontrole neurčitého integrálu, keď nie derivácia, ale diferenciál je prevzatý z odpovede:

V dôsledku toho získame nie integrand, ale integrand.

Nebojte sa konceptu diferenciálu.

Diferenciál je derivácia vynásobená dx.

Pre nás však nie sú dôležité teoretické jemnosti, ale čo ďalej s týmto diferenciálom. Rozdiel sa zobrazí nasledovne: ikona d odstrániť, dať ťah vpravo nad zátvorku, priradiť násobiteľa na koniec výrazu dx :

Prijaté iniciály integrand, to znamená, že integrál je nájdený správne.

Ako môžete vidieť, rozdiel spočíva v nájdení derivátu. Druhý spôsob kontroly sa mi páči menej, pretože musím dodatočne kresliť veľké zátvorky a ťahať ikonu diferenciálu dx do konca testu. Aj keď je to správnejšie, alebo "pevnejšie", alebo čo.

V skutočnosti sa o druhom spôsobe overovania dalo mlčať. Pointa nie je v metóde, ale v tom, že sme sa naučili otvárať diferenciál. Opäť.

Rozdiel sa prejavuje takto:

1) ikona d odstrániť;

2) umiestnite ťah vpravo nad zátvorku (označenie derivátu);

3) na koniec výrazu priradíme činiteľ dx .

Napríklad:

Zapamätaj si to. Uvažovanú techniku budeme veľmi skoro potrebovať.

Príklad 2

Keď nájdeme neurčitý integrál, VŽDY sa ho snažíme skontrolovať Navyše je na to skvelá príležitosť. Nie všetky typy úloh vo vyššej matematike sú z tohto pohľadu darom. Nezáleží na tom, že overenie sa pri kontrolných úlohách často nevyžaduje, nikto a nič nebráni tomu, aby sa vykonalo na návrhu. Výnimku možno urobiť len pri nedostatku času (napríklad na teste, skúške). Osobne vždy kontrolujem integrály a nedostatok overenia považujem za hack a zle splnenú úlohu.

Príklad 3

Nájdite neurčitý integrál:

. Spustite kontrolu.

Riešenie: Analýzou integrálu vidíme, že pod integrálom máme súčin dvoch funkcií a dokonca umocňujeme celý výraz. Bohužiaľ, na poli integrálnej bitky nie dobré a pohodlné vzorce na integráciu súčinu a kvocientu ako: alebo .

Preto, keď je daný súčin alebo kvocient, vždy má zmysel zistiť, či je možné transformovať integrand na súčet? Uvažovaný príklad je prípad, keď je to možné.

Najprv uvádzame úplné riešenie, komentáre budú uvedené nižšie.

(1) Používame starý dobrý vzorec štvorcového súčtu pre akékoľvek reálne čísla, čím sa zbavíme stupňa nad spoločnou zátvorkou. mimo zátvorky a použitím skráteného vzorca na násobenie v opačnom smere: .

Príklad 4

Nájdite neurčitý integrál

Spustite kontrolu.

Toto je príklad samoriešenia. Na konci lekcie odpovedzte a dokončite riešenie.

Príklad 5

Nájdite neurčitý integrál

. Spustite kontrolu.

V tomto príklade je integrand zlomkom. Keď vidíme zlomok v integrande, prvou myšlienkou by mala byť otázka: „Je možné sa tohto zlomku nejako zbaviť, alebo ho aspoň zjednodušiť?“.

Všimli sme si, že menovateľ obsahuje osamelý koreň „x“. Jeden v poli nie je bojovník, čo znamená, že čitateľa môžete rozdeliť na menovateľ výraz podľa výrazu:

Nekomentujeme akcie so zlomkovými mocninami, pretože sa o nich opakovane diskutovalo v článkoch o derivácii funkcie.

Ak vás stále mätie taký príklad ako

a nikto nedostane správnu odpoveď,

Všimnite si tiež, že riešenie preskočí jeden krok, a to uplatnenie pravidiel , . Zvyčajne, s určitými skúsenosťami s riešením integrálov, sa tieto pravidlá považujú za samozrejmú skutočnosť a nie sú podrobne opísané.

Príklad 6

Nájdite neurčitý integrál. Spustite kontrolu.

Toto je príklad samoriešenia. Na konci lekcie odpovedzte a dokončite riešenie.

Vo všeobecnom prípade so zlomkami v integráloch nie je všetko také jednoduché, ďalší materiál o integrácii zlomkov niektorých typov nájdete v článku: Integrácia niektorých zlomkov. Ale predtým, ako prejdete na vyššie uvedený článok, musíte si prečítať lekciu: Náhradná metóda v neurčitom integráli. Faktom je, že sčítanie funkcie pomocou diferenciálnej metódy alebo metódy premennej zmeny je kľúčový bod pri štúdiu témy, pretože sa nachádza nielen „v čistých úlohách náhradnej metódy“, ale aj v mnohých iných variantoch integrálov.

Riešenia a odpovede:

Príklad 2: Riešenie:

Príklad 4: Riešenie:

V tomto príklade sme použili vzorec zníženého násobenia

Príklad 6: Riešenie:

Metóda zmeny premennej v neurčitom integráli. Príklady riešení

V tejto lekcii sa zoznámime s jedným z najdôležitejších a najbežnejších trikov, ktorý sa používa pri riešení neurčitých integrálov - metódou zmeny premennej. Pre úspešné zvládnutie materiálu sú potrebné počiatočné znalosti a integračné zručnosti. Ak máte v integrálnom počte pocit prázdnej plnej čajovej kanvice, mali by ste sa najprv oboznámiť s materiálom Neurčitý integrál. Príklady riešení, kde je prístupnou formou vysvetlené, čo je to integrál a podrobne sú rozobraté základné príklady pre začiatočníkov.

Technicky je metóda zmeny premennej v neurčitom integráli implementovaná dvoma spôsobmi:

– Uvedenie funkcie pod znamenie diferenciálu.

– Skutočná zmena premennej.

V skutočnosti ide o to isté, no dizajn riešenia vyzerá inak. Začnime jednoduchším prípadom.