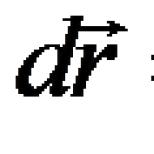شرط استقلال خطی بردارها. وابستگی خطی و استقلال بردارهای فضای خطی. وابستگی خطی و استقلال بردارهای فضایی سه بعدی. مبانی فضایی و سیستم مختصات وابسته

تعریف 18.2 سیستم عملکردf, ..., f pتماس گرفتلi-nape oساعت a in و c و m. o d در شکاف(آ، (3) اگر برخی غیر پیش پا افتاده است 5 ترکیب خطی این توابع برابر با صفر در این بازه به طور یکسان است:

تعریف 18.3 سیستم برداری f 1، ...، x n در a و c و m o d خطی نامیده می شود اگر ترکیبی خطی و غیر پیش پا افتاده از این بردارها با بردار گلوله برابر باشد:

Lبرای جلوگیری از سردرگمی، تعداد مولفه بردار (تابع-بردار) را با شاخص پایین و تعداد خود بردار (در صورت وجود چندین بردار از این قبیل) را با شاخص بالایی نشان خواهیم داد.

"به شما یادآوری می کنیم که اگر همه ضرایب موجود در آن صفر نباشند، یک ترکیب خطی غیر بی اهمیت نامیده می شود.

تعریف 18.4 سیستم توابع برداری x 1 ^)،...، x n (t) خطی نامیده می شودساعت و در و با و من در مورد هفتم در فاصله،(آ، /3) اگر ترکیبی خطی غیر بدیهی از این توابع برداری به طور یکسان برابر با بردار صفر در این بازه باشد:

درک ارتباط این سه مفهوم (وابستگی خطی توابع، بردارها و توابع برداری) با یکدیگر مهم است.

اول از همه، اگر فرمول (18.6) را به صورت بسط یافته ارائه کنیم (به یاد داشته باشید که هر یک از x g (1)بردار است)

آنگاه معادل نظام برابری ها خواهد بود

به معنای وابستگی خطی اجزای rth به معنای تعریف اول (به عنوان توابع). گفته می شود که وابستگی خطی توابع برداری دلالت بر آنها دارد جزء به جزءوابستگی خطی

عکس این قضیه به طور کلی درست نیست: کافی است مثال یک جفت توابع برداری را در نظر بگیریم

اولین اجزای این توابع برداری به سادگی بر هم منطبق هستند، به این معنی که آنها به صورت خطی وابسته هستند. مولفه های دوم متناسب هستند، بنابراین. به صورت خطی نیز وابسته هستند. با این حال، اگر سعی کنیم ترکیب خطی آنها را برابر با صفر به طور یکسان بسازیم، از رابطه

بلافاصله سیستم را دریافت کنید

که تنها راه حل دارد ج - ج-2 - 0. بنابراین، توابع برداری ما به صورت خطی مستقل هستند.

دلیل چنین ملک عجیبی چیست؟ ترفندی که به شما امکان می دهد توابع بردار مستقل خطی را از توابع وابسته آگاهانه بسازید چیست؟

به نظر می رسد که کل نقطه آنقدر در وابستگی خطی اجزا نیست، بلکه در نسبت ضرایبی است که برای به دست آوردن صفر ضروری است. در مورد وابستگی خطی توابع بردار، مجموعه یکسانی از ضرایب به همه اجزا، صرف نظر از تعداد آنها، خدمت می کند. اما در مثال ما، برای یک جزء، یک نسبت از ضرایب مورد نیاز بود، و برای دیگری، یک نسبت دیگر. بنابراین ترفند در واقع ساده است: برای به دست آوردن یک وابستگی خطی از کل توابع بردار از یک وابستگی خطی "مولفه به جزء"، لازم است که همه اجزا به صورت خطی "به یک نسبت" وابسته باشند.

اجازه دهید اکنون به بررسی رابطه بین وابستگی خطی توابع بردار و بردارها بپردازیم. در اینجا، تقریباً بدیهی است که وابستگی خطی توابع برداری دلالت بر این دارد که برای هر ثابت t*بردار

به صورت خطی وابسته خواهد بود.

برعکس، به طور کلی، صادق نیست: از وابستگی خطی بردارها برای هر یک تیاز وابستگی خطی توابع برداری پیروی نمی کند. این را در مثال دو تابع برداری به راحتی می توان مشاهده کرد

در t=1، t=2 و t=3جفت بردار به دست می آوریم

به ترتیب. هر جفت بردار متناسب است (به ترتیب با ضرایب 1،2 و 3). دیدن آن برای هر مشکلی آسان است t*جفت بردارهای ما با ضریب متناسب خواهند بود t*.

اگر بخواهیم یک ترکیب خطی از توابع برداری بسازیم که به طور یکسان برابر با صفر باشد، اولین مؤلفه ها قبلاً این رابطه را به ما می دهند.

که تنها در صورتی امکان پذیر است با = با2 = 0. بنابراین، توابع برداری ما به صورت خطی مستقل بودند. باز هم توضیح این اثر این است که در مورد وابستگی خطی توابع بردار، مجموعه ثابت های یکسان Cj به همه مقادیر خدمت می کند. تی،و در مثال ما برای هر مقدار تینسبت خود را بین ضرایب مورد نیاز است.

اجازه دهید توابع دارای مشتقاتی از حد (n-1) باشند.

تعیین کننده را در نظر بگیرید: (1)

W(x) تعیین کننده Wronsky برای توابع نامیده می شود.

قضیه 1.اگر توابع به صورت خطی در بازه (a, b) وابسته باشند، W(x) Wronskian آنها به طور یکسان برابر با صفر در این بازه است.

اثباتبا شرط قضیه، رابطه

، (2) که در آن همه برابر با صفر نیستند. بگذار باشد. سپس

(3). این هویت را n-1 بار متمایز کنید و

جایگزینی به جای مقادیر به دست آمده آنها در تعیین کننده ورونسکی،

ما گرفتیم:

(4).

در تعیین کننده Wronsky، آخرین ستون ترکیبی خطی از n-1 ستون های قبلی است و بنابراین در تمام نقاط بازه (a, b) صفر است.

قضیه 2.اگر توابع y1,…, yn راه حل های مستقل خطی معادله L[y] = 0 هستند که همه ضرایب آن در بازه (a, b) پیوسته هستند، ورونسکی این جواب ها در هر نقطه از معادله غیر صفر است. فاصله (الف، ب).

اثباتبیایید برعکس فرض کنیم. X0 وجود دارد که W(X0)=0 است. ما یک سیستم از n معادله می سازیم

(5).

بدیهی است که سیستم (5) یک راه حل غیر صفر دارد. اجازه دهید (6).

اجازه دهید یک ترکیب خطی از راه حل های y1،…، yn بسازیم.

Y(x) راه حلی برای معادله L[y] = 0 است. علاوه بر این، . بر اساس قضیه یکتایی، حل معادله L[y] = 0 با شرایط اولیه صفر فقط می تواند صفر باشد، یعنی .

ما هویت را دریافت می کنیم که در آن همه برابر با صفر نیستند، به این معنی که y1،…، yn به صورت خطی وابسته هستند، که با شرط قضیه در تضاد است. بنابراین، چنین نقطه ای وجود ندارد که W(X0)=0 باشد.

بر اساس قضیه 1 و قضیه 2، می توانیم ادعای زیر را فرموله کنیم. برای اینکه n راه حل معادله L[y] = 0 به صورت خطی مستقل در بازه (a, b) باشد، لازم و کافی است که ورونسکی آنها در هیچ نقطه ای از این بازه ناپدید نشود.

خصوصیات آشکار ورونسکی زیر نیز از قضایای اثبات شده به دست می آید.

1. اگر ورونسکی n راه حل معادله L[y] = 0 در یک نقطه x = x0 از بازه (a, b) که در آن همه ضرایب pi(x) پیوسته هستند برابر با صفر باشد، آنگاه برابر با صفر است. در تمام نقاط این فاصله
2. اگر ورونسکی n راه حل معادله L[y] = 0 در یک نقطه x = x0 از بازه (a, b) غیر صفر باشد، در تمام نقاط این بازه غیر صفر است.

بنابراین، برای خطی بودن n راه حل مستقل معادله L[y] = 0 در بازه (a, b)، که در آن ضرایب معادله pi(x) پیوسته است، لازم و کافی است که ورونسکی آنها باشد. حداقل در یک نقطه از این بازه غیر صفر است.

فضاهای خطی (بردار).

تعریف:یک دسته از Lتماس گرفت فضای خطی (بردار). ، اگر دو عملیات روی آن معرفی شود:

1) اضافه کردن: برای هر x، y Є Lجمع ( x + y) Є L,

2) ضرب در عدد: برای هر x Є Lو هر عدد λ محصول

λx Є L,

که 8 اصل را برآورده می کند:

1) x + y = y + x، جایی که x، y Є L;

2) (x + y) + z = x + (y + z)، جایی که x، y، z Є L;

3) یک عنصر صفر وجود دارد به طوری که Ө + x = x، جایی که x Є L;

4) برای هر x Є Lتنها یک عنصر مخالف وجود دارد

(-ایکس)به طوری که x + (-x) \u003d Ө;

5) 1 x = x، جایی که x Є L;

6) α(βх) = (αβ)х، جایی که x Є L، α و β اعداد هستند.

7) α(x + y) = αx + αy، جایی که x، y Є L, α - عدد;

8) (α + β) x = αx + βx، جایی که x Є L، α و β اعداد هستند.

اظهار نظر: عناصر یک فضای خطی (بردار) نامیده می شوند بردارها .

مثال ها:

مجموعه اعداد حقیقی یک فضای خطی است.

مجموعه تمام بردارها در صفحه و در فضا یک فضای خطی هستند.

مجموعه همه ماتریس های هم اندازه یک فضای خطی است.

در یک فضای خطی سیستمی از بردارها داده می شود a 1, a 2, a 3, ... a n Є L.

تعریف:بردار α 1 a 1 + α 2 a 2 +…+ α n a n Є L، جایی که یک من(i = 1،…،n) - اعداد، فراخوانی شده ترکیب خطی (LK) بردارهای a 1, a 2, a 3, ... a n.

تعریف:سیستم برداری فضای خطی a 1, a 2, a 3, ... a n Є Lتماس گرفت مستقل خطی (LNZ) اگر ترکیب خطی

α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n = 0اگر و فقط اگر ضرایب

α 1 =α 2 =α 3 =…=α n = 0.

تعریف:سیستم برداری a 1, a 2, a 3, ... a n Є Lتماس گرفت وابسته به خط (LZ) اگر مجموعه ای از اعداد وجود دارد α 1، α 2، α 3 … α n، که همه آنها برابر 0 نیستند، به طوری که ترکیب خطی α 1 a 1 + α 2 a 2 +…+ α n a n = 0.

مثال ها:

دو بردار نامیده می شوند خطیاگر موازی یک خط باشند یا روی یک خط قرار بگیرند.

1) دو بردار غیرصفر و غیر خطی را در صفحه در نظر بگیرید. مورب = 0 .

ترکیب خطی برابر با صفر است، یک ضریب غیر صفر وجود دارد، بنابراین، دو بردار خطی در هواپیما به صورت خطی وابسته هستند.

قضیه 1. شرط لازم و کافی برای وابستگی خطی.

برای اینکه سیستمی از بردارها در یک فضای خطی به صورت خطی وابسته باشد، لازم و کافی است که برخی از بردارهای این سیستم ترکیبی خطی از همه بردارهای دیگر باشد.

Doc-in: نیاز ().

با توجه به سیستم LZ. لازم است ثابت شود که یک بردار LC همه بردارهای دیگر است.

a 1, a 2, a 3, ... a n- سیستم بردارهای LZ، یعنی. بین α 1 ، α 2 ، α 3 ... α n عدد غیر صفر وجود دارد به طوری که LC α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n = 0.

فرض می کنیم که ضریب را تعیین کنیم α1 ≠ 0. دو طرف آخرین تساوی را بر تقسیم کنید α1 ≠ 0:

از این رو نتیجه می شود که یک 1- LC سایر بردارها.

نیاز ثابت شده است.

کفایت ().

بگذارید یک بردار ترکیبی خطی از بردارهای دیگر باشد. لازم است ثابت شود که سیستم بردارهای LZ.

بگذار باشد α n \u003d α 1 a 1 + α 2 a 2 + α 3 a 3 + ... + α n -1 a n -1.

α 1 a 1 + α 2 a 2 + α 3 a 3 + ... + α n -1 a n -1 - 1α n \u003d 0.

از آنجایی که یک ضریب غیر صفر وجود دارد، پس سیستم بردارها وجود دارد a 1, a 2, a 3, ... a nبه صورت خطی وابسته است

قضیه 2.یک سیستم حاوی بردار تهی به صورت خطی وابسته است.

Doc-in:سیستمی از بردارها حاوی بردار تهی را در نظر بگیرید. a 1, a 2, a 3, ... a n,Ө، جایی که Ө یک بردار تهی است. بدیهی است که برابری زیر برقرار است 0 а 1 + 0 а 2 + 0 а 3 +…+ 5 Ө = 0.

یک ضریب غیر صفر برابر با 5 وجود دارد و ترکیب خطی برابر با 0 است، از این رو سیستم بردارهای LZ نتیجه می شود.

قضیه 3.سیستمی که دارای یک زیرسیستم وابسته به خطی باشد نیز به صورت خطی وابسته خواهد بود.

Doc-in:سیستم بردارها را در نظر بگیرید a 1, a 2, ..., a k, a k+1 ... a n، جایی که a 1، a 2، ...، a kیک قطعه خطی وابسته است. α 1 a 1 + α 2 a 2 + ... + α k a k \u003d 0. ضریب دیگری غیر از صفر وجود دارد.

بدیهی است که با همان ضرایب برابری

α 1 a 1 + α 2 a 2 +…+α k a k +…+0 a k+1 +…+ 0 α n = 0.

از این رو نتیجه می شود که سیستم بردارهای LZ.

در این مقاله به موارد زیر خواهیم پرداخت:

• بردارهای خطی چیست؟
• شرایط برای بردارهای خطی چیست؟
• خواص بردارهای خطی چیست؟
• وابستگی خطی بردارهای خطی چقدر است.

بردارهای خطی بردارهایی هستند که موازی یک خط هستند یا روی یک خط قرار می گیرند.

مثال 1

شرایط برای بردارهای خطی

اگر هر یک از شرایط زیر درست باشد دو بردار هم خط هستند:

• شرط 1 . اگر عدد λ وجود داشته باشد به طوری که a = λ b باشد، بردارهای a و b هم خط هستند.
• شرط 2 . بردارهای a و b با نسبت مساوی از مختصات خطی هستند:

a = (a 1 ؛ a 2) ، b = (b 1 ؛ b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• شرط 3 . بردارهای a و b هم خط هستند به شرطی که حاصلضرب بردار و بردار صفر برابر باشند:

a ∥ b ⇔ a، b = 0

تبصره 1

شرط 2 اگر یکی از مختصات برداری صفر باشد، قابل استفاده نیست.

تبصره 2

شرط 3 فقط برای آن دسته از بردارهایی که در فضا داده شده اند قابل استفاده است.

نمونه هایی از مسائل برای مطالعه هم خطی بردارها

ما بردارهای a \u003d (1; 3) و b \u003d (2; 1) را برای همخطی بودن بررسی می کنیم.

چگونه تصمیم بگیریم؟

در این صورت لازم است از شرط 2 همخطی استفاده شود. برای بردارهای داده شده، به نظر می رسد:

برابری اشتباه است. از اینجا می توان نتیجه گرفت که بردارهای a و b غیر خطی هستند.

پاسخ : a | | ب

مثال 2

چه مقدار m از بردار a = (1 ; 2) و b = (- 1 ; m) برای هم خطی بودن بردارها لازم است؟

چگونه تصمیم بگیریم؟

با استفاده از شرط خطی دوم، بردارها در صورتی هم خط خواهند بود که مختصات آنها متناسب باشد:

این نشان می دهد که m = - 2 .

پاسخ: m = - 2 .

معیارهای وابستگی خطی و استقلال خطی سیستم های بردارها

سیستمی از بردارها در یک فضای برداری فقط زمانی به صورت خطی وابسته است که یکی از بردارهای سیستم را بتوان بر حسب بقیه بردارهای سیستم بیان کرد.

اثبات

اجازه دهید سیستم e 1 , e 2 , . . . ، e n به صورت خطی وابسته است. بیایید ترکیب خطی این سیستم را برابر با بردار صفر بنویسیم:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

که در آن حداقل یکی از ضرایب ترکیب برابر با صفر نباشد.

بگذارید a k ≠ 0 k ∈ 1, 2, . . . , n .

هر دو طرف تساوی را بر یک ضریب غیر صفر تقسیم می کنیم:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

مشخص کن:

A k - 1 a m , که در آن m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

در این مورد:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + βn e n = 0

یا e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

نتیجه این است که یکی از بردارهای سیستم بر حسب تمام بردارهای دیگر سیستم بیان می شود. چیزی که باید ثابت شود (p.t.d.).

کفایت

بگذارید یکی از بردارها به صورت خطی بر حسب تمام بردارهای دیگر سیستم بیان شود:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

بردار e k را به سمت راست این برابری منتقل می کنیم:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

از آنجایی که ضریب بردار e k برابر است با - 1 ≠ 0، ما یک نمایش غیر پیش پا افتاده صفر را با سیستمی از بردارهای e 1 , e 2 , دریافت می کنیم. . . ، e n ، و این به نوبه خود به این معنی است که سیستم داده شده از بردارها به صورت خطی وابسته است. چیزی که باید ثابت شود (p.t.d.).

نتیجه:

• یک سیستم از بردارها زمانی مستقل خطی است که هیچ یک از بردارهای آن را نتوان بر حسب تمام بردارهای دیگر سیستم بیان کرد.
• یک سیستم برداری که شامل یک بردار تهی یا دو بردار مساوی است به صورت خطی وابسته است.

ویژگی های بردارهای وابسته به خط

1. برای بردارهای 2 و 3 بعدی، این شرط محقق می شود: دو بردار وابسته خطی هم خط هستند. دو بردار خطی به صورت خطی وابسته هستند.
2. برای بردارهای سه بعدی، این شرط محقق می شود: سه بردار وابسته خطی همسطح هستند. (3 بردار همسطح - وابسته به خطی).
3. برای بردارهای n بعدی، این شرط محقق می شود: n + 1 بردار همیشه به صورت خطی وابسته هستند.

نمونه هایی از حل مسائل برای وابستگی خطی یا استقلال خطی بردارها

بیایید بردارهای a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 را برای استقلال خطی بررسی کنیم.

تصمیم گیری بردارها به صورت خطی وابسته هستند زیرا ابعاد بردارها کمتر از تعداد بردارها است.

مثال 4

بیایید بردارهای a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 را برای استقلال خطی بررسی کنیم.

تصمیم گیری مقادیر ضرایبی را پیدا می کنیم که در آنها ترکیب خطی برابر با بردار صفر خواهد بود:

x 1 a + x 2 b + x 3 c 1 = 0

معادله برداری را به صورت خطی می نویسیم:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

ما این سیستم را با استفاده از روش گاوس حل می کنیم:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

از خط 2 ما 1 را کم می کنیم ، از 3 - 1 را کم می کنیم:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

خط 2 را از خط 1 کم کنید، 2 را به 3 اضافه کنید:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

از راه حل نتیجه می شود که سیستم راه حل های زیادی دارد. این بدان معنی است که ترکیبی غیر صفر از مقادیر چنین اعداد x 1 , x 2 , x 3 وجود دارد که ترکیب خطی a , b , c برابر با بردار صفر است. بنابراین بردارهای a , b , c هستند وابسته به خط ​​​​​​​

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

فضای برداری مثال ها و ساده ترین خواص فضاهای برداری وابستگی خطی و استقلال سیستم بردارها اساس و رتبه یک سیستم متناهی از بردارها.

فضای خطی یا برداری L(P) روی فیلد P یک مجموعه غیر خالی L است که عملیات ها بر روی آن معرفی می شوند:

1. علاوه بر این، به هر جفت از عناصر مجموعه یک عنصر از همان مجموعه اختصاص داده می شود که با x + yεL نشان داده می شود.

2. ضرب در یک اسکالر (یعنی عنصری از میدان P)، یعنی هر عنصر λ ϵ P و هر عنصر x ε L با یک عنصر منفرد از L(P) مرتبط است که با λx ϵ L( نشان داده می شود. پ).

در این حالت، شرایط زیر برای عملیات اعمال می شود:

1. ایکس+ y= y+ x، برای هر x،y ϵ L.

2.ایکس+ (y + z) = (x + y) + z، x، y، z ε L. (تداعی انقباض)

3. چنین وجود دارد θ ϵ L، که ایکس+ θ =x برایهر x ε L (وجود یک عنصر خنثی با توجه به جمع)، به ویژه، خالی نیست.

4. برای هر x ϵ L یک عنصر -x ϵ L وجود دارد به طوری که ایکس+(-x)= θ (وجود عنصر مقابل نسبت به جمع).

5.(αβ)х=α(βх)، (تداعی ضرب در یک اسکالر)

6.1*x=x (وحدت: ضرب در عنصر خنثی (با ضرب) فیلد P بردار را حفظ می کند).

7.(α+ β)* x= α* x+ β*x، (توزیع ضرب در یک بردار با توجه به جمع اسکالرها)؛

8. α * (x + y) = α*x+ α *y، (توزیع ضرب در یک اسکالر با توجه به جمع بردار).

عناصر مجموعه L را بردار و عناصر میدان P را اسکالر می نامند. ویژگی های 1-4 با بدیهیات گروه آبلیان منطبق است.

ساده ترین قدیسان:

1. فضای برداری با جمع یک گروه آبلی است.

2. برای هر x ϵ L، عنصر مقابل -x ϵ L تنها عنصر است

3. 0*ایکس=θ، برای هر x ϵ L

4. 1*(-x)=-x برای هرکس x ϵ L

5.α * θ = θ ,برای هر αϵ L

نمونه ای از VP yav-Xia m \ در ماتریس‌هایی با مولفه‌های واقعی هم‌ترتیب با تعریف طبیعی از عملیات جمع و ضرب. ماتریس در تعداد ماده

وابستگی خطی \ (نه) سیستمی از بردارها (تعاریف، خصوصیات)

قضیه. (شرط لازم و کافی برای وابستگی خطی سیستم بردارها.)

سیستمی از بردارها در یک فضای برداری به صورت خطی وابسته است اگر و تنها در صورتی که یکی از بردارهای سیستم به صورت خطی بر حسب بردارهای دیگر این سیستم بیان شود.

اثبات نیاز. اجازه دهید سیستم e 1 ..e n به صورت خطی وابسته باشد. سپس، طبق تعریف، بردار تهی را به روشی غیر پیش پا افتاده نشان می دهد، یعنی. یک ترکیب خطی غیر پیش پا افتاده از این سیستم از بردارها برابر با بردار صفر وجود دارد:

α 1 e 1 +..+ α n e n = 0، که حداقل یکی از ضرایب این ترکیب خطی غیر صفر است. فرض کنید α k≠0,kϵ 1,2…n هر دو قسمت تساوی قبلی را بر این ضریب غیر صفر تقسیم کنید (یعنی ضرب در αk -1 *(α 1 e 1 +..+ αa n e n) = 0

نشان دهید: αk -1 α m =β m که در آن mϵ 1,2…,k-1,k+1,..,n سپس β 1 e 1+ … +β 1 e n = 0 یعنی. یکی از بردارهای سیستم به صورت خطی بر حسب سایر بردارهای این سیستم و غیره بیان می شود.

کفایت. بگذارید یکی از بردارهای سیستم به صورت خطی بر حسب بردارهای دیگر این سیستم بیان شود: e k =γ 1 e 1+..+ γ n e n

از آنجایی که ضریب در بردار e k برابر است با -1≠0، پس ما با سیستمی از بردارها e 1 ..e n نمایش غیر بدیهی صفر داریم که به این معنی است که این سیستم از بردارها به صورت خطی وابسته است و غیره.

قضیه ثابت شده است.

نتیجه.

1. یک سیستم از بردارها در یک فضای برداری به صورت خطی مستقل است اگر و تنها در صورتی که هیچ یک از بردارهای سیستم به صورت خطی بر حسب بردارهای دیگر این سیستم بیان نشود.

2. سیستمی از بردارها که حاوی یک بردار صفر یا دو بردار مساوی است به صورت خطی وابسته است.

نتیجه.

یک سیستم متشکل از یک بردار به صورت خطی مستقل است اگر و فقط اگر این بردار غیر صفر باشد.

پایه مجموعه ای از بردارها در یک فضای برداری است به طوری که هر بردار این فضا را می توان به طور منحصر به فرد به عنوان ترکیبی خطی از بردارها از این مجموعه - بردارهای پایه نشان داد.

تعداد بردارهای موجود در هر زیرسیستم خطی مستقل از یک سیستم معین از بردارها نامیده می شود. رتبهسیستم های.

قضیه.بگذارید دو سیستم داده شود پ-بردارهای بعدی:

آ 1 ,آ 2، ¼، آ r (9)

ب 1 ,ب 2، ¼، بس, (10)

لزوماً مستقل خطی نیست و رتبه سیستم (9) برابر با عدد است ک، رتبه سیستم (10) عدد است ل. اگر سیستم اول به صورت خطی بر حسب سیستم دوم بیان شود، پس k £ l. اگر اینها سیستم ها معادل هستند، سپس k = l.

تعداد عناصر (کاردینالیته) حداکثر زیرمجموعه مستقل خطی فضا به انتخاب این زیرمجموعه بستگی ندارد و رتبه یا بعد فضا نامیده می شود و خود این زیر مجموعه را پایه می نامند.