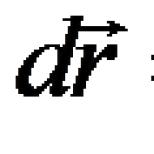چگونه می توان اساس یک سیستم معین از بردارها را پیدا کرد. وابستگی خطی اساس سیستم برداری اساس است

ترکیب خطی از بردارها یک بردار است
، که در آن λ 1 , ... , λ m ضرایب دلخواه هستند.

سیستم برداری
اگر ترکیب خطی آن برابر با وجود داشته باشد وابسته خطی نامیده می شود ، که حداقل یک ضریب غیر صفر دارد.

سیستم برداری
مستقل خطی نامیده می شود اگر در هر یک از ترکیبات خطی آن برابر باشد ، همه ضرایب صفر هستند.

اساس سیستم بردارها
زیرسیستم مستقل خطی غیر خالی آن نامیده می شود که از طریق آن می توان هر بردار سیستم را بیان کرد.

مثال 2. اساس سیستم بردارها را بیابید = (1, 2, 2, 4),= (2, 3, 5, 1),= (3, 4, 8, -2),= (2، 5، 0، 3) و بردارهای باقیمانده را بر اساس مبنا بیان کنید.

راه حل ما یک ماتریس می سازیم که در آن مختصات این بردارها را به صورت ستونی مرتب می کنیم. آن را به صورت پلکانی در می آوریم.

~
~
~
.

اساس این سیستم را بردارها تشکیل می دهند ,,، که با عناصر اصلی ردیف هایی که با دایره مشخص شده اند مطابقت دارد. برای یک عبارت برداری معادله x 1 را حل کنید +x2 +x4 =. به سیستم معادلات خطی تقلیل می‌یابد که ماتریس آن با جابجایی ستون مربوط به آن از نسخه اصلی به دست می‌آید. ، به جای ستون اصطلاحات آزاد. بنابراین برای حل سیستم از ماتریس به دست آمده به صورت گام به گام استفاده می کنیم و جایگشت های لازم را در آن انجام می دهیم.

ما متوالی پیدا می کنیم:

x 1 + 4 = 3، x 1 = -1;

= -+2.

نکته 1. اگر لازم باشد چندین بردار از طریق پایه بیان شود، برای هر یک از آنها سیستم معادلات خطی مربوطه ساخته می شود. این سیستم ها فقط در ستون های اعضای آزاد متفاوت خواهند بود. بنابراین، برای حل آنها می توان یک ماتریس را کامپایل کرد که در آن چندین ستون از اعضای آزاد وجود خواهد داشت. در این حالت هر سیستمی مستقل از سایرین حل می شود.

نکته 2. برای بیان هر بردار، فقط استفاده از بردارهای پایه سیستمی که قبل از آن هستند، کافی است. در این مورد، نیازی به تغییر شکل ماتریس نیست، کافی است یک خط عمودی را در جای مناسب قرار دهید.

تمرین 2. اساس سیستم بردارها را بیابید و بقیه بردارها را از طریق مبنا بیان کنید:

آ) = (1, 3, 2, 0),= (3, 4, 2, 1),= (1, -2, -2, 1),= (3, 5, 1, 2);

ب) = (2, 1, 2, 3),= (1, 2, 2, 3),= (3, -1, 2, 2),= (4, -2, 2, 2);

که در) = (1, 2, 3),= (2, 4, 3),= (3, 6, 6),= (4, -2, 1);= (2, -6, -2).

1. 3. سیستم تصمیم گیری اساسی

یک سیستم معادلات خطی همگن نامیده می شود که تمام عبارات آزاد آن برابر با صفر باشد.

سیستم اساسی راه حل های یک سیستم همگن معادلات خطی اساس مجموعه راه حل های آن است.

اجازه دهید یک سیستم ناهمگن از معادلات خطی داده شود. یک سیستم همگن مرتبط با یک معین، سیستمی است که از یک معین با جایگزینی تمام جمله های آزاد با صفر به دست می آید.

اگر یک سیستم ناهمگن ثابت و نامعین باشد، پس حل دلخواه آن به شکل f o1 +  1 f o1 + ... +  k f o k است، که در آن f o یک راه حل خاص از سیستم ناهمگن و f o1، ...، f o k است. راه حل های اساسی سیستم همگن مرتبط است.

مثال 3. یک راه حل خاص از سیستم ناهمگن را از مثال 1 و سیستم اساسی راه حل های سیستم همگن مرتبط پیدا کنید.

راه حل. حل به دست آمده در مثال 1 را به صورت برداری می نویسیم و بردار حاصل را به مجموع پارامترهای آزاد موجود در آن و مقادیر عددی ثابت گسترش می دهیم:

\u003d (x 1، x 2، x 3، x 4) \u003d (-2a + 7b - 2، a، -2b + 1، b) \u003d (-2a، a، 0، 0) + (7b، 0، - 2b، b) + +(– 2، 0، 1، 0) = a(-2، 1، 0، 0) + b(7، 0، -2، 1) + (– 2، 0، 1، 0).

f n = (- 2، 0، 1، 0)، f o1 = (-2، 1، 0، 0)، f o2 = (7، 0، -2، 1) دریافت می کنیم.

اظهار نظر. مشکل یافتن یک سیستم اساسی از راه حل ها برای یک سیستم همگن نیز به همین ترتیب حل می شود.

تمرین 3.1 سیستم اساسی راه حل های یک سیستم همگن را بیابید:

آ)

ب)

ج) 2x 1 - x 2 + 3x 3 \u003d 0.

تمرین 3.2. یک راه حل خاص از سیستم ناهمگن و سیستم اساسی راه حل های سیستم همگن مرتبط را پیدا کنید:

آ)

ب)

در هندسه، یک بردار به عنوان یک قطعه جهت دار درک می شود و بردارهایی که با ترجمه موازی از یکدیگر به دست می آیند برابر در نظر گرفته می شوند. همه بردارهای مساوی به عنوان بردار یکسان در نظر گرفته می شوند. ابتدای بردار را می توان در هر نقطه ای از فضا یا صفحه قرار داد.

اگر مختصات انتهای بردار در فضا داده شود: آ(ایکس 1 , y 1 , z 1), ب(ایکس 2 , y 2 , z 2) سپس

= (ایکس 2 – ایکس 1 , y 2 – y 1 , z 2 – z 1). (1)

فرمول مشابهی در هواپیما وجود دارد. این بدان معنی است که یک بردار را می توان به عنوان یک رشته مختصات نوشت. عملیات بردارها، - جمع و ضرب در یک عدد، روی رشته ها جزء به جزء انجام می شود. این امکان بسط مفهوم بردار را فراهم می کند و یک بردار را به عنوان هر رشته ای از اعداد درک می کند. به عنوان مثال، حل یک سیستم معادلات خطی و همچنین هر مجموعه ای از مقادیر متغیرهای سیستم را می توان به عنوان یک بردار در نظر گرفت.

در رشته هایی با طول یکسان، عملیات جمع بر اساس قانون انجام می شود

(a 1 , a 2 , … , a n) + (b 1 , b 2 , … , b n) = (a 1 + b 1 , a 2 + b 2 , … , a n+b n). (2)

ضرب یک رشته در یک عدد طبق قانون انجام می شود

l(a 1 , a 2 , … , a n) = (la 1 , la 2 , … , la n). (3)

مجموعه ای از بردارهای ردیف با طول معین nبا اعمال نشان داده شده جمع بردار و ضرب در یک عدد، ساختار جبری به نام فضای خطی n بعدی.

ترکیب خطی از بردارها یک بردار است ، جایی که λ 1 , ... , λ مترضرایب دلخواه هستند.

سیستمی از بردارها را در صورتی وابسته خطی می نامند که ترکیب خطی آن برابر با 1 وجود داشته باشد که حداقل یک ضریب غیر صفر داشته باشد.

سیستمی از بردارها به صورت مستقل خطی نامیده می‌شود که در هر یک از ترکیب‌های خطی آن برابر با، همه ضرایب صفر باشند.

بنابراین، حل مسئله وابستگی خطی سیستم بردارها به حل معادله کاهش می یابد.

ایکس 1 + ایکس 2 + … + x m = . (4)

اگر این معادله دارای راه حل های غیر صفر باشد، سیستم بردارها به صورت خطی وابسته است. اگر جواب صفر منحصر به فرد باشد، سیستم بردارها مستقل خطی است.

برای حل سیستم (4)، برای وضوح، بردارها را می توان نه به صورت ردیف، بلکه به صورت ستون نوشت.

سپس پس از انجام تبدیلات در سمت چپ به سیستم معادلات خطی معادل معادله (4) می رسیم. ماتریس اصلی این سیستم از مختصات بردارهای اصلی که در ستون ها چیده شده اند تشکیل می شود. ستون اعضای آزاد در اینجا مورد نیاز نیست، زیرا سیستم همگن است.

اساسسیستم بردارها (متناهی یا نامتناهی، به ویژه، کل فضای خطی) زیرسیستم مستقل خطی غیر خالی آن است که از طریق آن می توان هر بردار سیستم را بیان کرد.

مثال 1.5.2.اساس سیستم بردارها را بیابید = (1، 2، 2، 4)، = (2، 3، 5، 1)، = (3، 4، 8، -2)، = (2، 5، 0، 3) و سایر بردارها را از طریق پایه بیان کنید.

تصمیم گیری. ماتریسی می سازیم که در آن مختصات این بردارها به صورت ستونی چیده شده اند. این ماتریس سیستم است ایکس 1 + ایکس 2 + ایکس 3 + ایکس 4 = . ماتریس را به شکل پلکانی می آوریم:

~ ~ ~

اساس این سیستم از بردارها توسط بردارهای , , , که مربوط به عناصر اصلی ردیف هایی است که با دایره مشخص شده اند تشکیل می شود. برای بیان بردار، معادله را حل می کنیم ایکس 1 + ایکس 2 + ایکس 4 = . به سیستمی از معادلات خطی تقلیل می‌یابد که ماتریس آن از اصل با مرتب کردن مجدد ستون مربوط به، به محل ستون عبارت‌های آزاد به دست می‌آید. بنابراین، هنگام کاهش به یک فرم پله‌ای، همان تبدیل‌های فوق روی ماتریس انجام می‌شود. این بدان معنی است که ما می توانیم با ایجاد جایگشت های لازم برای ستون های موجود در آن، ماتریس حاصل را به صورت پلکانی استفاده کنیم: ستون های دارای دایره در سمت چپ نوار عمودی قرار می گیرند و ستون مربوط به بردار در سمت راست قرار می گیرد. از نوار

ما متوالی پیدا می کنیم:

ایکس 4 = 0;

ایکس 2 = 2;

ایکس 1 + 4 = 3, ایکس 1 = –1;

اظهار نظر. اگر لازم باشد چندین بردار از طریق پایه بیان شود، برای هر یک از آنها سیستم معادلات خطی مربوطه ساخته می شود. این سیستم ها فقط در ستون های اعضای آزاد متفاوت خواهند بود. در این حالت هر سیستمی مستقل از سایرین حل می شود.

تمرین 1.4.اساس سیستم بردارها را بیابید و بقیه بردارها را بر اساس مبنا بیان کنید:

a) = (1، 3، 2، 0)، = (3، 4، 2، 1)، = (1، –2، –2، 1)، = (3، 5، 1، 2);

ب) = (2، 1، 2، 3)، = (1، 2، 2، 3)، = (3، -1، 2، 2)، = (4، -2، 2، 2)؛

ج) = (1، 2، 3)، = (2، 4، 3)، = (3، 6، 6)، = (4، -2، 1); = (2، -6، -2).

در یک سیستم معین از بردارها، یک پایه معمولاً می تواند به روش های مختلف متمایز شود، اما همه پایه ها دارای تعداد یکسانی بردار خواهند بود. به تعداد بردارها در پایه یک فضای خطی، بعد فضا می گویند. برای nفضای خطی بعدی nبعد فضا است، زیرا این فضا دارای مبنای استاندارد = (1، 0، …، 0)، = (0، 1، …، 0)، …، = (0، 0، …، 1) است. از این طریق، هر بردار = (a 1 , a 2 , … , a n) به صورت زیر بیان می شود:

= (a 1 , 0 , … , 0) + (0, a 2 , … , 0) + … + (0, 0, … , a n) =

A 1 (1، 0، …، 0) + a 2 (0، 1، …، 0) + … + a n(0, 0, ... ,1) = a 1 + a 2 + ... + a n .

بنابراین، اجزای ردیف بردار = (a 1 , a 2 , … , a n) ضرایب آن در بسط بر حسب مبنای استاندارد می باشد.

خطوط مستقیم در هواپیما

مسئله هندسه تحلیلی استفاده از روش مختصات در مسائل هندسی است. بنابراین، مسئله به شکل جبری ترجمه شده و با استفاده از جبر حل می شود.

بیان فرم تماس گرفت ترکیب خطی بردارها A 1 , A 2 ,...,A nبا ضرایب λ 1، λ 2،...، λ n.

تعیین وابستگی خطی یک سیستم از بردارها

سیستم برداری A 1 , A 2 ,...,A nتماس گرفت وابسته به خط, اگر مجموعه ای از اعداد غیر صفر وجود داشته باشد λ 1، λ 2،...، λ n, که تحت آن ترکیب خطی بردارها λ 1 *A 1 +λ 2 *A 2 +...+λ n *A nبرابر با بردار صفریعنی سیستم معادلات: راه حل غیر صفر دارد.
مجموعه اعداد λ 1، λ 2،...، λ n اگر حداقل یکی از اعداد غیر صفر است λ 1، λ 2،...، λ n متفاوت از صفر

تعیین استقلال خطی یک سیستم از بردارها

سیستم برداری A 1 , A 2 ,...,A nتماس گرفت مستقل خطی، اگر ترکیب خطی این بردارها باشد λ 1 *A 1 +λ 2 *A 2 +...+λ n *A nفقط برای یک مجموعه صفر از اعداد برابر با بردار صفر است λ 1، λ 2،...، λ n یعنی سیستم معادلات: A 1 x 1 +A 2 x 2 +...+A n x n =Θیک راه حل صفر منحصر به فرد دارد.

بررسی کنید که آیا سیستمی از بردارها به صورت خطی وابسته است یا خیر

تصمیم گیری:

1. ما یک سیستم معادلات می سازیم:

2. با استفاده از روش گاوس آن را حل می کنیم. تغییرات اردن سیستم در جدول 29.1 آورده شده است. هنگام محاسبه، قسمت های مناسب سیستم یادداشت نمی شوند، زیرا آنها برابر با صفر هستند و تحت تبدیل جردن تغییر نمی کنند.

3. از سه ردیف آخر جدول ما سیستم مجاز را معادل اصلی می نویسیمسیستم:

4. ما راه حل کلی سیستم را دریافت می کنیم:

5. با تعیین مقدار متغیر آزاد x 3 =1 به اختیار خود، ما یک راه حل غیر صفر خاص به دست می آوریم X=(-3،2،1).

پاسخ: بنابراین، با یک مجموعه اعداد غیر صفر (-3،2،1)، ترکیب خطی بردارها برابر با بردار صفر -3A 1 +2A 2 +1A 3 =Θ است. از این رو، سیستم بردارهای وابسته خطی.

ویژگی های سیستم های برداری

اموال (1)
اگر سیستم بردارها به صورت خطی وابسته باشد، حداقل یکی از بردارها بر حسب بقیه تجزیه می شود و بالعکس، اگر حداقل یکی از بردارهای سیستم بر حسب بقیه تجزیه شود، سیستم بردارها به صورت خطی وابسته است.

اموال (2)
اگر هر زیر سیستمی از بردارها به صورت خطی وابسته باشد، کل سیستم به صورت خطی وابسته است.

اموال (3)
اگر سیستمی از بردارها مستقل خطی باشد، هر یک از زیرسیستم‌های آن مستقل خطی است.

اموال (4)
هر سیستم بردار حاوی بردار صفر به صورت خطی وابسته است.

اموال (5)
اگر تعداد بردارها n بیشتر از بعد آنها باشد (n>m) سیستمی از بردارهای m بعدی همیشه به صورت خطی وابسته است.

اساس سیستم برداری

اساس سیستم بردارها A 1 , A 2 ,..., A n چنین زیر سیستمی است B 1 , B 2 ,...,B r(هر یک از بردارهای B 1 ,B 2 ,...,B r یکی از بردارهای A 1 , A 2 ,..., A n است) که شرایط زیر را برآورده می کند:
1. B 1 ,B 2 ,...,B rسیستم بردارهای مستقل خطی؛
2. هر بردار A j از سیستم A 1 , A 2 ,..., A n به صورت خطی بر حسب بردارهای B 1 ,B 2 ,...,B r بیان می شود.

rتعداد بردارهای موجود در پایه است.

قضیه 29.1 بر اساس واحد سیستم بردارها.

اگر سیستمی از بردارهای m بعدی حاوی m بردار واحد مختلف E 1 E 2 ,..., E m باشد، آنگاه آنها اساس سیستم را تشکیل می دهند.

الگوریتمی برای یافتن اساس یک سیستم بردار

برای یافتن اساس سیستم بردارهای A 1 ,A 2 ,...,A n لازم است:

• یک سیستم همگن از معادلات متناظر با سیستم بردارها بسازید A 1 x 1 +A 2 x 2 +...+A n x n =Θ
• این سیستم را بیاورید

اساس سیستم بردارها و بردارهایی که در مبنا گنجانده نشده اند را بیابید، بر اساس آن بسط دهید:

آ 1 = {5, 2, -3, 1}, آ 2 = {4, 1, -2, 3}, آ 3 = {1, 1, -1, -2}, آ 4 = {3, 4, -1, 2}, آ 5 = {13, 8, -7, 4}.

تصمیم گیری. یک سیستم همگن از معادلات خطی را در نظر بگیرید

آ 1 ایکس 1 + آ 2 ایکس 2 + آ 3 ایکس 3 + آ 4 ایکس 4 + آ 5 ایکس 5 = 0

یا گسترش یافته است.

ما این سیستم را با استفاده از روش گاوسی، بدون جابجایی سطرها و ستون ها، و علاوه بر این، انتخاب عنصر اصلی نه در گوشه بالا سمت چپ، بلکه در سراسر ردیف حل خواهیم کرد. وظیفه این است که قسمت مورب سیستم تبدیل شده بردارها را انتخاب کنید.

~ ~

~ ~ ~ .

سیستم مجاز از بردارها که معادل بردار اصلی است دارای فرم است

آ 1 1 ایکس 1 + آ 2 1 ایکس 2 + آ 3 1 ایکس 3 + آ 4 1 ایکس 4 + آ 5 1 ایکس 5 = 0 ,

جایی که آ 1 1 = , آ 2 1 = , آ 3 1 = , آ 4 1 = , آ 5 1 = . (1)

بردارها آ 1 1 , آ 3 1 , آ 4 1 یک سیستم مورب را تشکیل می دهند. از این رو بردارها آ 1 , آ 3 , آ 4 اساس سیستم بردارها را تشکیل می دهند آ 1 , آ 2 , آ 3 , آ 4 , آ 5 .

اکنون بردارها را گسترش می دهیم آ 2 و آ 5 بر اساس آ 1 , آ 3 , آ 4 . برای این کار ابتدا بردارهای مربوطه را گسترش می دهیم آ 2 1 و آ 5 1 سیستم مورب آ 1 1 , آ 3 1 , آ 4 1، با توجه به اینکه ضرایب انبساط برداری در سیستم مورب مختصات آن است. x i.

از (1) داریم:

آ 2 1 = آ 3 1 (-1) + آ 4 1 0 + آ 1 1 1 آ 2 1 = آ 1 1 – آ 3 1 .

آ 5 1 = آ 3 1 0 + آ 4 1 1 + آ 1 1 2 آ 5 1 = 2آ 1 1 + آ 4 1 .

بردارها آ 2 و آ 5 گسترش در اساس آ 1 , آ 3 , آ 4 با ضرایبی مشابه بردارها آ 2 1 و آ 5 1 سیستم مورب آ 1 1 , آ 3 1 , آ 4 1 (آن ضرایب x i). از این رو،

آ 2 = آ 1 – آ 3 , آ 5 = 2آ 1 + آ 4 .

وظایف یکیاساس سیستم بردارها را بیابید و بردارهایی که در مبنا قرار نمی گیرند، بر اساس مبنا بسط دهید:

1. آ 1 = { 1, 2, 1 }, آ 2 = { 2, 1, 3 }, آ 3 = { 1, 5, 0 }, آ 4 = { 2, -2, 4 }.

2. آ 1 = { 1, 1, 2 }, آ 2 = { 0, 1, 2 }, آ 3 = { 2, 1, -4 }, آ 4 = { 1, 1, 0 }.

3. آ 1 = { 1, -2, 3 }, آ 2 = { 0, 1, -1 }, آ 3 = { 1, 3, 0 }, آ 4 = { 0, -7, 3 }, آ 5 = { 1, 1, 1 }.

4. آ 1 = { 1, 2, -2 }, آ 2 = { 0, -1, 4 }, آ 3 = { 2, -3, 3 }.

2. تمام پایه های یک سیستم بردار را بیابید:

1. آ 1 = { 1, 1, 2 }, آ 2 = { 3, 1, 2 }, آ 3 = { 1, 2, 1 }, آ 4 = { 2, 1, 2 }.

2. آ 1 = { 1, 1, 1 }, آ 2 = { -3, -5, 5 }, آ 3 = { 3, 4, -1 }, آ 4 = { 1, -1, 4 }.