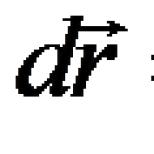ویژگی نامحدود محدودیت عملکرد عملکرد صعودی و کاهشی

توجه داشته باشید که تمام تعاریف شامل یک مجموعه عددی X است که بخشی از دامنه تابع است: X با D(f). در عمل، اغلب مواردی وجود دارد که X یک بازه عددی است (بخش، بازه، پرتو و غیره).

تعریف 1.

تابع y \u003d f (x) در مجموعه X با D (f) افزایش می یابد اگر برای هر دو نقطه x 1 و x 2 از مجموعه X به طوری که x 1 باشد.< х 2 , выполняется неравенство f(х 1 < f(х 2).

تعریف 2.

تابع y \u003d f (x) در مجموعه ایکس کاهنده با D (f) نامیده می شود اگر برای هر یکنواختی دو نقطه x 1 و x 2 از مجموعه X، به طوری که x 1< х 2 , функции выполняется неравенство f(x 1) >f (x2).

در عمل، استفاده از فرمول های زیر راحت تر است: اگر مقدار بزرگتر آرگومان با مقدار بزرگتر تابع مطابقت داشته باشد، تابع افزایش می یابد. اگر مقدار بزرگتر آرگومان با مقدار کوچکتر تابع مطابقت داشته باشد، تابع کاهش می یابد.

در کلاس های هفتم و هشتم، از تفسیر هندسی زیر از مفاهیم افزایش یا کاهش توابع استفاده کردیم: با حرکت در امتداد نمودار یک تابع افزایشی از چپ به راست، به نوعی از تپه بالا می رویم (شکل 55). حرکت در امتداد نمودار یک تابع کاهشی از چپ به راست، انگار که از تپه ای پایین می رویم (شکل 56).
معمولاً اصطلاحات "تابع افزایشی" ، "تابع کاهشی" با نام رایج تابع یکنواخت متحد می شوند و مطالعه یک تابع برای افزایش یا کاهش را مطالعه تابع برای یکنواختی می نامند.

ما به یک مورد دیگر توجه می کنیم: اگر یک تابع در حوزه طبیعی خود در حال افزایش (یا کاهش) باشد، معمولاً گفته می شود که تابع در حال افزایش (یا کاهش) است - بدون تعیین مجموعه عددی X.

مثال 1

تابع یکنواختی را بررسی کنید:

آ) y \u003d x 3 + 2; ب) y \u003d 5 - 2x.

تصمیم:

الف) مقادیر دلخواه آرگومان x 1 و x 2 را بگیرید و اجازه دهید x 1 باشد<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

آخرین نابرابری به این معنی است که f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).

بنابراین از x 1< х 2 следует f(х 1) >f(x 2)، به این معنی که تابع داده شده در حال کاهش است (در کل خط اعداد).

تعریف 3.

تابع y - f(x) از پایین در مجموعه X با D (f) نامیده می شود اگر همه مقادیر تابع در مجموعه X بزرگتر از یک عدد خاص باشد (به عبارت دیگر، اگر یک عدد وجود داشته باشد عدد m طوری که برای هر مقدار x є X نابرابری f( x) >m).

تعریف 4.

تابع y \u003d f (x) از بالا در مجموعه X با D (f) نامیده می شود اگر همه مقادیر تابع کمتر از یک عدد معین باشند (به عبارت دیگر، اگر عدد M وجود داشته باشد به طوری که برای هر مقدار x є X نابرابری f (x)< М).

اگر مجموعه X مشخص نشده باشد، فرض می شود که تابع از پایین یا از بالا در کل دامنه تعریف محدود شده است.

اگر تابعی هم از پایین و هم از بالا محدود شود، آن را محدود می نامند.

مرزبندی یک تابع به راحتی از نمودار آن خوانده می شود: اگر تابع از پایین محدود شده باشد، نمودار آن کاملاً بالای یک خط افقی y \u003d m قرار دارد (شکل 57). اگر تابع از بالا محدود شده باشد، نمودار آن کاملاً در زیر یک خط افقی y \u003d M قرار دارد (شکل 58).

مثال 2تابعی را برای مرزبندی بررسی کنید
تصمیم گیریاز یک طرف، نابرابری کاملاً آشکار است (با تعریف جذر، این بدان معنی است که تابع از زیر محدود می شود. از طرف دیگر، ما داریم و بنابراین
این بدان معنی است که تابع از بالا محدود شده است. حال به نمودار تابع داده شده نگاه کنید (شکل 52 از پاراگراف قبل). مرزبندی تابع هم از بالا و هم از پایین به راحتی از نمودار خوانده می شود.

تعریف 5.

عدد m کوچکترین مقدار تابع y \u003d f (x) در مجموعه X C D (f) نامیده می شود، اگر:

1) در X چنین نقطه ای x 0 وجود دارد که f(x 0) = m.

2) برای همه x از X نابرابری m>f(х 0) برآورده می شود.

تعریف 6.

عدد M بزرگترین مقدار تابع y \u003d f (x) در مجموعه X C D (f) نامیده می شود، اگر:
1) در X چنین نقطه ای x 0 وجود دارد که f(x 0) = M.
2) برای همه x از X، نابرابری
ما کوچکترین مقدار تابع را در کلاس هفتم و هشتم با نماد y و بزرگترین مقدار را با نماد y نشان دادیم.

اگر مجموعه X مشخص نشده باشد، فرض بر این است که ما در مورد یافتن کوچکترین یا بزرگترین مقدار تابع در کل دامنه تعریف صحبت می کنیم.

عبارات مفید زیر کاملا واضح است:

1) اگر تابعی دارای Y باشد، از زیر محدود می شود.
2) اگر تابعی دارای Y باشد، از بالا محدود می شود.
3) اگر تابع زیر محدود نشده باشد، Y وجود ندارد.
4) اگر تابع از بالا محدود نشده باشد، Y وجود ندارد.

مثال 3

کوچکترین و بزرگترین مقادیر یک تابع را پیدا کنید
تصمیم گیری

کاملاً واضح است، به خصوص اگر به نمودار تابع (شکل 52) متوسل شوید که \u003d 0 (این تابع در نقاط x \u003d -3 و x \u003d 3 به این مقدار می رسد)، a \u003d 3 ( تابع در نقطه x \u003d 0 به این مقدار می رسد.
در کلاس هفتم و هشتم به دو خاصیت دیگر از توابع اشاره کردیم. اولی خاصیت تحدب یک تابع نام داشت. در نظر گرفته می شود که تابعی در بازه X به سمت پایین محدب است اگر با اتصال هر دو نقطه از نمودار آن (با ابسیسا از X) با یک پاره خط مستقیم، متوجه شویم که قسمت مربوط به نمودار در زیر پاره ترسیم شده قرار دارد. شکل 59). پیوستگی یک تابع در بازه X به سمت بالا محدب است اگر با اتصال هر دو نقطه از نمودار آن (با ابسیسا از X) توسط یک پاره خط مستقیم، متوجه شویم که قسمت مربوطه از نمودار بالای قطعه ترسیم شده قرار دارد (شکل 60). ).

خاصیت دوم - پیوستگی تابع در بازه X - به این معنی است که نمودار تابع در بازه X پیوسته است، یعنی. بدون سوراخ و پرش

اظهار نظر.

در حقیقت ، همانطور که می گویند ، در ریاضیات همه چیز "دقیقاً برعکس" است: نمودار یک تابع به صورت یک خط جامد (بدون سوراخ و پرش) تنها زمانی نشان داده می شود که تداوم تابع ثابت شود. اما تعریف رسمی از تداوم یک تابع، که کاملاً پیچیده و ظریف است، هنوز از توان ما خارج است. همین را می توان در مورد تحدب یک تابع نیز گفت. با بحث در مورد این دو ویژگی توابع، ما همچنان به بازنمایی های بصری-شهودی تکیه خواهیم کرد.

حال بیایید دانش خود را مرور کنیم. با یادآوری توابعی که در کلاس های هفتم و هشتم مطالعه کردیم، نحوه ظاهر نمودارهای آنها را روشن خواهیم کرد و ویژگی های تابع را با رعایت نظم خاصی فهرست می کنیم، به عنوان مثال: دامنه تعریف. یکنواخت؛ محدودیت؛ , تداوم؛ محدوده مقادیر؛ محدب

متعاقباً، ویژگی‌های جدید توابع ظاهر می‌شوند و لیست ویژگی‌ها بر این اساس تغییر می‌کند.

1. تابع ثابت y \u003d C

نمودار تابع y \u003d C در شکل نشان داده شده است. 61 - خط مستقیم، موازی با محور x. این یک تابع غیر جالب است که لیست کردن ویژگی های آن بی معنی است.

نمودار تابع y \u003d kx + m یک خط مستقیم است (شکل 62، 63).

ویژگی های تابع y \u003d kx + m:

1)
2) اگر k > 0 افزایش می یابد (شکل 62)، اگر k کاهش می یابد< 0 (рис. 63);

4) نه بزرگترین و نه کوچکترین مقادیر وجود دارد.
5) تابع پیوسته است.
6)
7) صحبت در مورد تحدب معنی ندارد.

نمودار تابع y \u003d kx 2 سهمی است با راس در مبدا و با شاخه هایی که در صورت k\u003e O (شکل 64) به سمت بالا و اگر k به سمت پایین هدایت می شوند.< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

ویژگی های تابع y - kx 2:

برای مورد k > 0 (شکل 64):

1) D(f) = (-oo،+oo);


4) = وجود ندارد.
5) مستمر؛
6) Е(f) = تابع کاهش می یابد، و در بازه، در پرتو کاهش می یابد.
7) محدب به سمت بالا.

نمودار تابع y \u003d f (x) نقطه به نقطه ساخته می شود. هر چه نقاط بیشتری از شکل (x؛ f (x)) بگیریم، ایده دقیق تری از نمودار بدست می آوریم. اگر تعداد زیادی از این نکات را در نظر بگیریم، ایده نمودار کاملتر می شود. در این حالت است که شهود به ما می گوید که نمودار باید به صورت یک خط ثابت رسم شود (در این مورد به صورت سهمی). و سپس، با خواندن نمودار، در مورد تداوم تابع، در مورد تحدب آن به سمت پایین یا بالا، در مورد محدوده تابع نتیجه می گیریم. باید بدانید که از هفت ملک ذکر شده، فقط اموال 1)، 2، 3، 4) "قانونی" هستند به این معنا که می توانیم با مراجعه به تعاریف دقیق آنها را اثبات کنیم. ما فقط بازنمایی بصری-شهودی در مورد خواص باقی مانده داریم. اتفاقاً هیچ اشکالی ندارد. از تاریخ توسعه ریاضیات، مشخص شده است که بشر اغلب و برای مدت طولانی از خواص مختلف اشیاء خاص استفاده می کند، بدون اینکه تعاریف دقیق را بداند. پس از آن که چنین تعاریفی قابل تدوین بود، همه چیز در جای خود قرار گرفت.

نمودار تابع یک هذلولی است، محورهای مختصات به عنوان مجانبی از هذلول عمل می کنند (شکل 66، 67).

1) D(f) = (-00.0)1U (0.+oo);
2) اگر k > 0 باشد، تابع در پرتو باز (-oo، 0) و در پرتو باز (0، +oo) کاهش می یابد (شکل 66). اگر به< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) نه از پایین و نه از بالا محدود نمی شود.
4) نه کوچکترین و نه بزرگترین مقادیر وجود دارد.
5) تابع در پرتو باز (-oo، 0) و در پرتو باز (0، +oo) پیوسته است.
6) E(f) = (-oo، 0) U (0، + oo);
7) اگر k > 0 باشد، تابع در x به سمت بالا محدب است< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0، یعنی روی تیر باز (0, +oo) (شکل 66). اگر به< 0, то функция выпукла вверх при х >o و در x به پایین محدب می شوند< О (рис. 67).
نمودار تابع شاخه ای از سهمی است (شکل 68). ویژگی های تابع:
1) D(f) = ، در پرتو افزایش می یابد و در بازه ( آ;ب) سپس یک نکته وجود دارد که

قضیه کوشی.

اگر توابع f(x) و g(x) در بازه پیوسته باشند و در بازه (a, b) و g¢(x) 1 0 در بازه (a, b) قابل تمایز باشند، حداقل یک وجود دارد. نقطه e، a< e < b, такая, что

آن ها نسبت افزایش توابع در یک بخش معین برابر است با نسبت مشتقات در نقطه e. نمونه هایی از درس حل مسئله محاسبه حجم جسم از نواحی شناخته شده مقاطع موازی آن حساب انتگرال

نمونه هایی از کار البتهمهندسی برق

برای اثبات این قضیه در نگاه اول استفاده از قضیه لاگرانژ بسیار راحت است. فرمول تفاضل محدود را برای هر تابع بنویسید و سپس آنها را بر یکدیگر تقسیم کنید. با این حال، این دیدگاه اشتباه است، زیرا نقطه e برای هر یک از توابع به طور کلی متفاوت است. البته، در برخی موارد خاص، این نقطه از فاصله ممکن است برای هر دو تابع یکسان باشد، اما این یک تصادف بسیار نادر است، نه یک قاعده، و بنابراین نمی توان برای اثبات قضیه استفاده کرد.

اثبات تابع کمکی را در نظر بگیرید

هنگامی که x→x 0، مقدار c نیز به x 0 تمایل دارد. اجازه دهید در تساوی قبلی به حد گذر کنیم:

مانند ، سپس .

بنابراین

(حد نسبت دو بینهایت کوچک برابر است با حد نسبت مشتقات آنها در صورت وجود دومی)

قانون L'Hopital، در ∞ / ∞.

قضیه حد تابع یکنواخت. اثبات قضیه با استفاده از دو روش ارائه می شود. تعاریفی از توابع به شدت افزایشی، غیر کاهشی، شدیداً کاهشی و غیرافزاینده نیز ارائه شده است. تعریف تابع یکنواخت

عملکرد از بالا محدود نمی شود

1.1. عدد b متناهی باشد: .
1.1.2. اجازه دهید تابع از بالا نامحدود باشد.

.

در .

بیایید نشان دهیم. سپس برای هر وجود دارد، به طوری که
در .
این بدان معناست که حد سمت چپ در نقطه b است (به "تعریف حدود نامتناهی یک طرفه یک تابع در نقطه پایانی مراجعه کنید").

b اوایل به اضافه بی نهایت

عملکرد از بالا محدود شده است

1. اجازه دهید تابع در بازه کاهش نمی یابد.
1.2.1. اجازه دهید تابع از بالا با عدد M محدود شود: برای.
اجازه دهید ثابت کنیم که در این مورد یک محدودیت وجود دارد.

از آنجایی که تابع از بالا محدود شده است، یک کران بالایی محدود وجود دارد
.
با توجه به تعریف حداقل کران بالا، شرایط زیر برآورده می شود:
;
برای هر مثبت استدلالی برای آن وجود دارد
.

از آنجایی که تابع کاهش نمی یابد، پس برای . سپس در . یا
در .

بنابراین ما دریافتیم که برای هر یک عدد وجود دارد، به طوری که
در .
"تعریف حدود یک طرفه در بی نهایت").

عملکرد از بالا محدود نمی شود

1. اجازه دهید تابع در بازه کاهش نمی یابد.
1.2. عدد b به اضافه بی نهایت باشد: .
1.2.2. اجازه دهید تابع از بالا نامحدود باشد.
اجازه دهید ثابت کنیم که در این مورد یک محدودیت وجود دارد.

از آنجایی که تابع از بالا محدود نشده است، برای هر عدد M یک آرگومان وجود دارد که برای آن
.

از آنجایی که تابع کاهش نمی یابد، پس برای . سپس در .

بنابراین، برای هر یک عدد وجود دارد، به طوری که
در .
این بدان معنی است که حد در است (به "تعریف محدودیت های بی نهایت یک طرفه در بی نهایت" مراجعه کنید).

عملکرد افزایش نمی یابد

حال حالتی را در نظر بگیرید که تابع در حال افزایش نیست. همانطور که در بالا گفته شد می توانید هر گزینه را جداگانه در نظر بگیرید. اما ما بلافاصله آنها را پوشش خواهیم داد. برای این ما استفاده می کنیم. اجازه دهید ثابت کنیم که در این مورد یک محدودیت وجود دارد.

کران پایینی متناهی مجموعه مقادیر تابع را در نظر بگیرید:
.
در اینجا B می تواند یک عدد محدود یا یک نقطه در بی نهایت باشد. با توجه به تعریف infimum دقیق، شرایط زیر برآورده می شود:
;
برای هر همسایگی نقطه B استدلالی برای آن وجود دارد
.
با شرط قضیه، . بنابراین .

از آنجایی که تابع افزایش نمی یابد، پس برای . از آن به بعد
در .
یا
در .
علاوه بر این، ما توجه می کنیم که نابرابری همسایگی سوراخ شده سمت چپ نقطه b را تعریف می کند.

بنابراین، دریافتیم که برای هر همسایگی نقطه، یک همسایگی چپ سوراخ شده از نقطه b وجود دارد که
در .
این بدان معناست که حد سمت چپ در نقطه b این است:

(به تعریف جهانی حد یک تابع طبق کوشی مراجعه کنید).

محدودیت در نقطه a

حالا بیایید نشان دهیم که در نقطه a حدی وجود دارد و مقدار آن را پیدا کنیم.

بیایید یک تابع را در نظر بگیریم. با شرط قضیه، تابع یکنواخت است. بیایید متغیر x را با - x جایگزین کنیم (یا جایگزینی را انجام دهیم و سپس متغیر t را با x جایگزین کنیم). سپس تابع یکنواخت برای . ضرب نابرابری ها در -1 و با تغییر ترتیب آنها، نتیجه می گیریم که تابع برای .

به همین ترتیب، به راحتی می توان نشان داد که اگر کاهش نیابد، افزایش نمی یابد. سپس با توجه به آنچه در بالا ثابت شد، حدی وجود دارد
.
اگر زیاد نشد پس کم نمی شود. در این صورت محدودیتی وجود دارد
.

اکنون باید نشان دهیم که اگر محدودیتی برای تابع در وجود داشته باشد، در این صورت محدودیتی برای تابع در وجود دارد و این حدود برابر هستند:
.

بیایید نماد را معرفی کنیم:
(1) .
بیایید f را برحسب g بیان کنیم:
.
یک عدد مثبت دلخواه بگیرید. بگذارید یک همسایگی اپسیلونی نقطه A وجود داشته باشد. همسایگی اپسیلون برای مقادیر متناهی و نامتناهی A تعریف شده است (به "همسایگی یک نقطه" مراجعه کنید). از آنجایی که حد (1) وجود دارد، پس با توجه به تعریف حد، برای هر یک چنین وجود دارد که
در .

بگذارید یک عدد محدود باشد. اجازه دهید همسایگی سوراخ شده سمت چپ نقطه -a را با استفاده از نابرابری ها بیان کنیم:
در .
بیایید x را با -x جایگزین کنیم و این را در نظر بگیریم:
در .
دو نابرابری آخر یک همسایه سمت راست سوراخ شده نقطه a را تعریف می کنند. سپس
در .

بگذارید a یک عدد نامتناهی باشد، . بحث را تکرار می کنیم.
در ;
در ;
در ;
در .

بنابراین، ما دریافتیم که برای هر چیزی چنین وجود دارد
در .
این به آن معنا است
.

قضیه ثابت شده است.

اگر چنین عددی وجود داشته باشد، تابع y=f(x) BOUNDED UP (BOTTOM) را در مجموعه A از دامنه D(f) فراخوانی می کنیم. م ، که برای هر x از این شرط را تنظیم کنید

با استفاده از نمادهای منطقی، تعریف را می توان به صورت زیر نوشت:

f(x) – از بالا در مجموعه محدود شده است

(f(x) – از پایین در مجموعه محدود شده است

توابع محدود شده در مقدار مطلق یا به سادگی محدود نیز در نظر گرفته می شوند.

اگر یک عدد مثبت M وجود داشته باشد، تابع BOUNDED در مجموعه A را از دامنه تعریف فراخوانی می کنیم.

به زبان نمادهای منطقی

f(x) – محدود در مجموعه

تابعی که محدود نباشد نامحدود نامیده می شود. می دانیم که تعاریف ارائه شده از طریق نفی محتوای کمی دارند. برای فرمول بندی این ادعا به عنوان یک تعریف، از ویژگی های عملیات کمیت (3.6) و (3.7) استفاده می کنیم. سپس انکار کران بودن تابع در زبان نمادهای منطقی به دست خواهد آمد:

f(x) – محدود در مجموعه

نتیجه به دست آمده به ما امکان می دهد تعریف زیر را فرموله کنیم.

یک تابع در مجموعه A نامحدود نامیده می شود که متعلق به دامنه تابع است، اگر در این مجموعه برای هر عدد مثبت M چنین مقداری از آرگومان x وجود داشته باشد. , که مقدار همچنان از مقدار M فراتر خواهد رفت، یعنی .

به عنوان مثال، تابع را در نظر بگیرید

بر روی کل محور واقعی تعریف شده است. اگر قطعه [–2;1] (مجموعه A) را بگیریم، بر روی آن هم از بالا و هم از پایین محدود می شود.

در واقع، برای نشان دادن اینکه از بالا محدود است، باید محمول را در نظر بگیریم

و نشان دهید که M وجود دارد (وجود دارد) به طوری که برای تمام x های گرفته شده در قطعه [–2;1]، درست خواهد بود.

پیدا کردن چنین M کار دشواری نیست. می‌توانیم M = 7 را فرض کنیم، کمیت‌گر وجود مستلزم یافتن حداقل یک مقدار از M است. وجود چنین M این واقعیت را تأیید می‌کند که تابع در بخش [–2;1] از بالا محدود شده است.

برای اثبات کران بودن آن از پایین، باید محمول را در نظر بگیریم

مقدار M که صدق این گزاره را تضمین می کند، برای مثال M = -100 است.

می توان ثابت کرد که تابع نیز به صورت مدول محدود می شود: برای همه x از قطعه [–2;1]، مقادیر تابع با مقادیر انطباق دارد، بنابراین، به عنوان M، می توانیم بگیریم. به عنوان مثال، مقدار قبلی M = 7.

اجازه دهید نشان دهیم که همان تابع، اما در بازه، نامحدود خواهد بود، یعنی

برای نشان دادن وجود چنین x، عبارت را در نظر بگیرید

با جستجوی مقادیر مورد نیاز x در بین مقادیر مثبت آرگومان، به دست می آوریم

این بدان معناست که مهم نیست که Mwe چه مثبتی می گیرد، مقادیر x که تحقق نابرابری را تضمین می کند.

از نسبت به دست می آیند.

با در نظر گرفتن یک تابع در کل محور واقعی، می توان نشان داد که در قدر مطلق نامحدود است.

در واقع، از نابرابری

یعنی مهم نیست که M مثبت چقدر بزرگ باشد یا تحقق نابرابری را تضمین می کند.

عملکرد فوق العاده.

تابع در نقطه است با حداکثر محلی (حداقل) اگر چنین همسایگی از این نقطه وجود داشته باشد که برای ایکس¹ با این محله نابرابری را ارضا می کند

مخصوصاً اینکه نقطه منتهی فقط می تواند یک نقطه داخلی شکاف باشد و f(x) باید در آن تعریف شود. موارد احتمالی عدم وجود اکستروموم در شکل 1 نشان داده شده است. 8.8.

اگر یک تابع در یک بازه زمانی افزایش (کاهش) و در یک بازه زمانی کاهش (افزایش) شود، آن نقطه با حداکثر (حداقل) نقطه محلی است.

عدم وجود حداکثر تابع f(x) در یک نقطه با می توان اینگونه فرمول بندی کرد:

_______________________

f(x) حداکثر در c دارد

این بدان معنی است که اگر نقطه c یک نقطه حداکثر محلی نباشد، مهم نیست که همسایگی که نقطه c را به عنوان یک داخلی در بر می گیرد، حداقل یک مقدار x وجود دارد که برابر با c نیست، که برای آن . بنابراین، اگر در نقطه c ماکزیمم وجود نداشته باشد، ممکن است در این نقطه اصلاً اکستروم وجود نداشته باشد، یا ممکن است یک نقطه حداقل باشد (شکل 8.9).

مفهوم اکستروم یک ارزیابی مقایسه ای از مقدار یک تابع در هر نقطه در رابطه با تابع های نزدیک به دست می دهد. مقایسه مشابهی از مقادیر تابع را می توان برای تمام نقاط یک بازه انجام داد.

GREATEST (MINIMUM) مقدار یک تابع در یک مجموعه مقدار آن در نقطه ای از این مجموعه است به طوری که – برای . بیشترین مقدار تابع در نقطه داخلی قطعه و کوچکترین مقدار بدست می آید – در انتهای چپ آن

برای تعیین بزرگترین (کوچکترین) مقدار یک تابع داده شده در یک قطعه، لازم است که بزرگترین (کوچکترین) عدد را از بین تمام مقادیر حداکثر (حداقل) آن و همچنین مقادیر در نظر گرفته شده در آن انتخاب کنید. انتهای فاصله این بزرگترین (کوچکترین) مقدار تابع خواهد بود. این قانون بعدا مشخص خواهد شد.

مشکل یافتن بزرگترین و کوچکترین مقادیر یک تابع در بازه باز همیشه به راحتی حل نمی شود. به عنوان مثال، تابع

در فاصله (شکل 8.11) آنها را ندارد.

برای مثال مطمئن شویم که این تابع بیشترین مقدار را ندارد. در واقع، با توجه به یکنواختی تابع، می توان استدلال کرد که هر چقدر هم که مقادیر x را به سمت چپ واحد نزدیک کنیم، x دیگری وجود خواهد داشت که در آن مقادیر تابع بیشتر از مقادیر آن در نقاط ثابت داده شده، اما هنوز کمتر از واحد است.