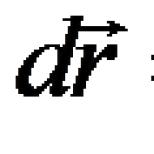مشتقات جزئی 3 متغیر. مشتقات جزئی مرتبه اول. دیفرانسیل کامل به طور مشابه، افزایش جزئی z را نسبت به y بدست می آوریم
توابع دو متغیر، مشتقات جزئی، دیفرانسیل و گرادیان
مبحث 5.توابع دو متغیر
مشتقات جزئی
تعریف تابع از دو متغیر، راه های تنظیم.
مشتقات خصوصی.
تابع گرادیان یک متغیر
یافتن بزرگترین و کوچکترین مقادیر یک تابع از دو متغیر در یک ناحیه محدود بسته
1. تعریف تابع از چند متغیر، راه های تنظیم
برای توابع دو متغیر
حوزه تعریف
مقداری است مجموعه ای از نقاط در یک هواپیما
و محدوده، شکاف روی محور است 
.
برای یک نمایش بصری توابع دو متغیر nyh اعمال شود خطوط سطح.
مثال
.
برای عملکرد 
یک نمودار و خطوط تراز بسازید. معادله یک خط تراز که از یک نقطه می گذرد را بنویسید 
.
نمودار تابع خطیهست یک سطحدر فضای.
برای یک تابع، نمودار صفحه ای است که از نقاط عبور می کند 
, 
, 
.
خطوط سطح عملکردخطوط موازی هستند که معادله آنها 
.
برای تابع خطی دو متغیر
خطوط سطح توسط معادله داده می شود 
و نمایندگی کنند خانواده ای از خطوط موازی در صفحه.
4
نمودار تابع 0 1 2 X
خطوط سطح ویژگی
Proi خصوصیتوابع مشتق دو متغیر
تابع را در نظر بگیرید 
. بیایید یک متغیر بدهیم 
در نقطه 
افزایش دلخواه 
، ترک مقدار متغیر 
بدون تغییر. افزایش تابع مربوطه
تماس گرفت افزایش جزئی یک تابع توسط متغیردر نقطه 
.
به طور مشابه تعریف شده است افزایش جزئی یک تابعتوسط متغیر: .
تعیینمشتق جزئی با توجه به: 
, 
,
, 
.
مشتق جزئی یک تابع با توجه به یک متغیر 
حد نامیده می شود :
نام گذاری ها: 
, 
,
, 
.
برای یافتن مشتق جزئی 
با توجه به یک متغیر، از قوانین تمایز یک تابع از یک متغیر استفاده می شود. با فرض ثابت بودن متغیر
به طور مشابه، برای یافتن مشتق جزئی با توجه به یک متغیر متغیر ثابت در نظر گرفته می شود 
.
مثال
. برای عملکرد 
مشتقات جزئی را پیدا کنید 
, 
و مقادیر آنها را در یک نقطه محاسبه کنید 
.
مشتق جزئی یک تابع 
توسط متغیر با این فرض ثابت است:
مشتق جزئی تابع را با فرض ثابت بودن آن بیابید:
اجازه دهید مقادیر مشتقات جزئی را محاسبه کنیم 
, 
:
; 
.
مشتقات جزئی مرتبه دوم توابع چندین متغیر را مشتقات جزئی مشتقات جزئی مرتبه اول می نامند.
بیایید مشتقات جزئی مرتبه دوم را برای تابع بنویسیم:
; 
;
; 
.
; 
و غیره.
اگر مشتقات جزئی مختلط تابعی از چندین متغیر در نقطه ای پیوسته باشند 
، سپس آنها برابر یکدیگردر این نقطه بنابراین، برای تابعی از دو متغیر، مقادیر مشتقات جزئی مختلط به ترتیب تمایز بستگی ندارد:
.
مثال.
برای یک تابع، مشتقات جزئی مرتبه دوم را پیدا کنید 
و 
.
تصمیم گیری
مشتق جزئی مختلط با تمایز متوالی اول تابع پیدا می شود 
با توجه به (با فرض ثابت)، سپس مشتق را متمایز می کنیم 
توسط (با فرض ثابت).
مشتق ابتدا با متمایز کردن تابع با توجه به و سپس مشتق با توجه به .
مشتقات جزئی مختلط با یکدیگر برابرند: 
.
3. گرادیان یک تابع از دو متغیر
خواص گرادیان
مثال
. یک تابع داده شده است 
. گرادیان را پیدا کنید 
در نقطه 
و آن را بسازید.
تصمیم گیری
مختصات گرادیان - مشتقات جزئی را پیدا کنید.
در نقطه 
شیب
برابر است با . شروع وکتور 
در نقطه و پایان در نقطه .
5 
4. یافتن بزرگترین و کوچکترین مقادیر یک تابع از دو متغیر در یک منطقه محدود بسته
فرمول بندی مسئله.
یک دامنه محدود بسته را در هواپیما بگذارید 
توسط سیستمی از نابرابری های شکل داده می شود 
. لازم است نقاطی را در منطقه ای که تابع بزرگترین و کوچکترین مقدار را می گیرد پیدا کنید.
مهم است مشکل افراطی، که مدل ریاضی آن شامل خطیمحدودیت ها (معادلات، نابرابری ها) و خطیعملکرد 
.
فرمول بندی مسئله.
بزرگترین و کوچکترین مقادیر یک تابع را پیدا کنید 
(2.1)
تحت محدودیت
(2.2)
. (2.3)
از آنجایی که هیچ نقطه بحرانی برای تابع خطی بسیاری از متغیرها وجود ندارد داخلمناطق 
، سپس راه حل بهینه ای که تابع هدف را با یک اکسترموم فراهم می کند، تنها به دست می آید در حاشیه منطقه. برای ناحیه ای که با محدودیت های خطی تعریف می شود، نقاط انتهایی ممکن هستند نقاط گوشه. این به ما اجازه می دهد تا راه حل مشکل را در نظر بگیریم روش گرافیکی.
حل گرافیکی سیستم نابرابری های خطی
برای حل این مشکل به صورت گرافیکی، باید بتوان سیستم های نابرابری های خطی را با دو متغیر به صورت گرافیکی حل کرد.
روش:
توجه داشته باشید که نابرابری 
تعریف می کند نیم صفحه مختصات راست(از محور 
) و نابرابری 
- نیم صفحه مختصات بالایی(از محور 
).
مثال.
حل نابرابری گرافیکی 
.
معادله خط مرزی را می نویسیم 
و آن را از دو نقطه بسازید، برای مثال، 
و 
. یک خط مستقیم یک صفحه را به دو نیم صفحه تقسیم می کند.
مختصات نقطه 
ارضای نابرابری ( 
درست است)، به این معنی که مختصات تمام نقاط نیم صفحه حاوی نقطه نابرابری را برآورده می کند. حل نابرابری مختصات نقاط نیم صفحه واقع در سمت راست خط مرزی شامل نقاط روی مرز خواهد بود. نیم صفحه مورد نظر در شکل مشخص شده است.
تصمیم گیری 
سیستم نابرابری نامیده می شود قابل قبول، اگر مختصات آن غیر منفی باشد، . مجموعه راه حل های قابل قبول برای سیستم نابرابری ها ناحیه ای را تشکیل می دهد که در ربع اول صفحه مختصات قرار دارد.
مثال. ناحیه حل سیستم نابرابری ها را بسازید
راه حل های نابرابری ها عبارتند از:
1) 
- نیم صفحه واقع در سمت چپ و پایین نسبت به خط مستقیم ( 
) 
;
2) 
نیم صفحه ای است که در نیم صفحه سمت راست پایین نسبت به خط مستقیم قرار دارد ( 
) 
;
3) 
- نیم صفحه واقع در سمت راست خط مستقیم ( 
) 
;
4) - یک نیم صفحه بالای محور آبسیسا، یعنی یک خط مستقیم ( 
) 
.
0 
دامنه راه حل های قابل قبولسیستم داده شده از نابرابری های خطی مجموعه نقاطی است که در داخل و روی مرز چهارضلعی قرار دارند. 
، که است تقاطعچهار هواپیمای نیمه
نمایش هندسی یک تابع خطی
(خطوط سطح و گرادیان)
بیایید مقدار را ثابت کنیم 
، معادله را بدست می آوریم 
، که از نظر هندسی یک خط مستقیم را مشخص می کند. در هر نقطه، تابع مستقیم مقدار می گیرد 
و است خط سطحدادن 
مقادیر مختلف، به عنوان مثال، 
، ... ، مجموعه ای از خطوط سطح را دریافت می کنیم - مجموعه موازی
مستقیم.
بیایید بسازیم شیب- بردار 
که مختصات آن برابر با مقادیر ضرایب متغیرهای تابع است 
. این بردار عبارت است از: 1) عمود بر هر خط مستقیم (خط تراز) 
; 2) جهت افزایش تابع هدف را نشان می دهد.
مثال
. خطوط سطح طرح و گرادیان ویژگی 
.
خطوط سطح در , , مستقیم هستند 
, 
, 
, به موازات یکدیگر. گرادیان بردار عمود بر هر خط سطح است.
یافتن گرافیکی بزرگترین و کوچکترین مقادیر یک تابع خطی در یک منطقه
بیان هندسی مسئله در حوزه حل سیستم نابرابری های خطی، نقطه ای را که خط تراز از آن می گذرد، مربوط به بزرگترین (کوچک ترین) مقدار یک تابع خطی با دو متغیر بیابید.
ترتیب دهی:
4. با حل سیستم معادلات خطوط متقاطع در نقطه A مختصات نقطه A را بیابید و کوچکترین مقدار تابع را محاسبه کنید. 
. به طور مشابه - برای نقطه B و بزرگترین مقدار تابع 
. ساخته شده بر روی points.variables خصوصیمشتقاتکارکردچندین متغیرهاو تکنیک تمایز نقاط بحرانی کارکرددومتغیرهاو لازمش...
هر مشتق جزئی (بیش از ایکسو توسط y) یک تابع از دو متغیر مشتق معمولی یک تابع از یک متغیر با مقدار ثابت متغیر دیگر است:
(جایی که y= ثابت)،
(جایی که ایکس= ثابت).
بنابراین، مشتقات جزئی از محاسبه می شود فرمول ها و قوانین برای محاسبه مشتقات توابع یک متغیر، در حالی که متغیر دیگر را ثابت (ثابت) در نظر می گیریم.
اگر نیازی به تجزیه و تحلیل مثال ها و حداقل تئوری لازم برای این ندارید، بلکه تنها به راه حلی برای مشکل خود نیاز دارید، پس ماشین حساب مشتق جزئی آنلاین .
اگر تمرکز روی پیگیری محل ثابت در تابع دشوار است، می توانید هر عددی را در حل پیش نویس مثال به جای متغیری با مقدار ثابت جایگزین کنید - سپس می توانید به سرعت مشتق جزئی را به عنوان یک عدد معمولی محاسبه کنید. مشتق تابع یک متغیر فقط لازم است فراموش نکنید که ثابت (متغیر با مقدار ثابت) را هنگام اتمام به جای خود برگردانید.
ویژگی مشتقات جزئی که در بالا توضیح داده شد از تعریف مشتق جزئی ناشی می شود که در سؤالات امتحانی یافت می شود. بنابراین برای آشنایی با تعریف زیر می توانید مرجع نظری را باز کنید.
مفهوم تداوم یک تابع z= f(ایکس, y) در یک نقطه مشابه این مفهوم برای تابعی از یک متغیر تعریف شده است.
عملکرد z = f(ایکس, y) در یک نقطه اگر پیوسته نامیده می شود
تفاوت (2) را افزایش کل تابع می گویند z(با افزایش هر دو آرگومان به دست می آید).
اجازه دهید تابع z= f(ایکس, y) و نقطه
اگر تابع تغییر کند zزمانی اتفاق می افتد که فقط یکی از آرگومان ها تغییر کند، برای مثال، ایکس، با مقدار ثابت آرگومان دیگر y، سپس تابع افزایش می یابد
افزایش جزئی تابع نامیده می شود f(ایکس, y) بر ایکس.
با توجه به تغییر تابع zبسته به تغییر تنها یکی از آرگومان ها، در واقع به تابعی از یک متغیر منتقل می کنیم.
اگر حد محدودی وجود دارد
سپس مشتق جزئی تابع نامیده می شود f(ایکس, y) با استدلال ایکسو با یکی از نمادها نشان داده می شود
(4)
افزایش جزئی به طور مشابه تعریف می شود zبر y:
و مشتق جزئی f(ایکس, y) بر y:
(6)
مثال 1
تصمیم گیری مشتق جزئی را با توجه به متغیر "x" پیدا می کنیم:
(yدرست شد)؛
مشتق جزئی را با توجه به متغیر "y" پیدا می کنیم:
(ایکسدرست شد).
همانطور که می بینید، فرقی نمی کند که تا چه حد متغیر ثابت است: در این مورد، فقط یک عدد است که یک عامل (مانند مشتق معمول) با متغیری است که با آن مقدار جزئی را پیدا می کنیم. مشتق. اگر متغیر ثابت در متغیری که مشتق جزئی آن را پیدا می کنیم ضرب نشود، این ثابت تنها، مهم نیست که تا چه حد، مانند یک مشتق معمولی، از بین می رود.
مثال 2یک تابع داده شده است
مشتقات جزئی را پیدا کنید
(با x) و (با y) و مقادیر آنها را در نقطه محاسبه کنید ولی (1; 2).
تصمیم گیری در یک ثابت yمشتق جمله اول به عنوان مشتق تابع توان یافت می شود ( جدول توابع مشتق یک متغیر):
.
در یک ثابت ایکسمشتق جمله اول به عنوان مشتق تابع نمایی و دومی - به عنوان مشتق ثابت یافت می شود:
اکنون مقادیر این مشتقات جزئی را در نقطه محاسبه می کنیم ولی (1; 2):
شما می توانید حل مشکلات با مشتقات جزئی را بررسی کنید ماشین حساب مشتق جزئی آنلاین .
مثال 3مشتقات جزئی توابع را بیابید
تصمیم گیری در یک مرحله پیدا می کنیم
(y ایکسگویا برهان سینوس 5 است ایکس: به همین ترتیب، 5 قبل از علامت تابع ظاهر می شود).
(ایکسثابت است و در این مورد عاملی در y).
شما می توانید حل مشکلات با مشتقات جزئی را بررسی کنید ماشین حساب مشتق جزئی آنلاین .
مشتقات جزئی یک تابع از سه یا چند متغیر به طور مشابه تعریف می شوند.
اگر هر مجموعه از مقادیر ( ایکس; y; ...; تی) متغیرهای مستقل از مجموعه دیمربوط به یک مقدار خاص است تواز بسیاری E، سپس توتابعی از متغیرها نامیده می شود ایکس, y, ..., تیو نشان دهند تو= f(ایکس, y, ..., تی).
برای توابع سه یا چند متغیر، هیچ تفسیر هندسی وجود ندارد.
مشتقات جزئی تابعی از چندین متغیر نیز با این فرض که تنها یکی از متغیرهای مستقل تغییر می کند، در حالی که بقیه ثابت هستند، تعریف و محاسبه می شوند.
مثال 4مشتقات جزئی توابع را بیابید
.
تصمیم گیری yو zدرست شد:
ایکسو zدرست شد:
ایکسو yدرست شد:
مشتقات جزئی را خودتان پیدا کنید و سپس راه حل ها را ببینید
مثال 5
مثال 6مشتقات جزئی یک تابع را بیابید.
مشتق جزئی تابعی از چندین متغیر یکسان است معنای مکانیکی به عنوان مشتق تابعی از یک متغیر، سرعتی است که تابع نسبت به تغییر در یکی از آرگومان ها تغییر می کند.
مثال 8مقدار جریان پمسافران راه آهن را می توان به عنوان یک تابع بیان کرد
جایی که پ- تعداد مسافران ن- تعداد ساکنان نقاط مربوطه، آر- فاصله بین نقاط
مشتق جزئی یک تابع پبر آرمساوی با
نشان می دهد که کاهش جریان مسافران با مجذور فاصله بین نقاط متناظر برای همان تعداد ساکن در نقاط نسبت معکوس دارد.
مشتق جزئی پبر نمساوی با
نشان می دهد که افزایش جریان مسافر متناسب با دو برابر تعداد ساکنان شهرک هایی با فاصله یکسان بین نقاط است.
شما می توانید حل مشکلات با مشتقات جزئی را بررسی کنید ماشین حساب مشتق جزئی آنلاین .
دیفرانسیل کامل
حاصلضرب مشتق جزئی و افزایش متغیر مستقل مربوطه را دیفرانسیل جزئی می گویند. دیفرانسیل های جزئی به صورت زیر نشان داده می شوند:
مجموع دیفرانسیل های جزئی بر روی همه متغیرهای مستقل، دیفرانسیل کل را نشان می دهد. برای تابعی از دو متغیر مستقل، دیفرانسیل کل با برابری بیان می شود
(7)
مثال 9دیفرانسیل کامل یک تابع را پیدا کنید
تصمیم گیری نتیجه استفاده از فرمول (7):
تابعی که دارای دیفرانسیل کلی در هر نقطه از دامنه باشد، در آن حوزه متمایز نامیده می شود.
دیفرانسیل کل را خودتان پیدا کنید و سپس راه حل را ببینید
همانطور که در مورد یک تابع از یک متغیر، تمایزپذیری یک تابع در یک منطقه خاص، مستلزم تداوم آن در این منطقه است، اما نه برعکس.
اجازه دهید بدون اثبات شرط کافی برای تمایزپذیری یک تابع را فرموله کنیم.
قضیه.اگر تابع z= f(ایکس, y) مشتقات جزئی پیوسته دارد
در یک منطقه معین، در این ناحیه قابل تفکیک است و دیفرانسیل آن با فرمول (7) بیان می شود.
می توان نشان داد که همانطور که در مورد تابعی از یک متغیر، دیفرانسیل تابع قسمت خطی اصلی افزایش تابع است، در مورد تابعی از چندین متغیر، دیفرانسیل کل اصلی، خطی با توجه به افزایش متغیرهای مستقل، بخشی از افزایش کل تابع.
برای تابعی از دو متغیر، افزایش کل تابع دارای شکل است
(8)
که در آن α و β برای و بی نهایت کوچک هستند.
مشتقات جزئی از مرتبه های بالاتر
مشتقات و توابع جزئی f(ایکس, y) خود برخی از توابع متغیرهای یکسان هستند و به نوبه خود ممکن است مشتقاتی نسبت به متغیرهای مختلف داشته باشند که به آنها مشتقات جزئی مرتبه بالاتر می گویند.
تعریف 1.11اجازه دهید تابعی از دو متغیر داده شود z=z(x,y), (x,y)D . نقطه م 0 (ایکس 0 ;y 0 ) - نقطه داخلی منطقه دی .
اگر در دی چنین محله ای وجود دارد UM 0 نکته ها م 0 ، که برای تمام نقاط
سپس اشاره کنید م 0 نقطه حداکثر محلی نامیده می شود. اما خود معنا z(M 0 ) - حداکثر محلی
اما اگر برای همه نکات
سپس اشاره کنید م 0 حداقل نقطه محلی تابع نامیده می شود z(x,y) . اما خود معنا z(M 0 ) - حداقل محلی
ماکزیمم محلی و حداقل محلی را منتهی الیه محلی تابع می نامند z(x,y) . روی انجیر 1.4 معنای هندسی حداکثر محلی را توضیح می دهد: م 0 حداکثر نقطه است، زیرا در سطح است z=z(x,y) نقطه متناظر آن سی 0 بالاتر از هر نقطه همسایه است سی (این محل حداکثر است).
توجه داشته باشید که نقاطی روی سطح به طور کلی وجود دارد (به عنوان مثال، AT ) که در بالا هستند سی 0 ، اما این نکات (مثلا AT ) "مجاور" نقطه نیستند سی 0 .
به طور خاص، نکته AT با مفهوم حداکثر جهانی مطابقت دارد:
حداقل جهانی به طور مشابه تعریف می شود:
یافتن حداکثر و حداقل جهانی در بخش 1.10 مورد بحث قرار خواهد گرفت.
قضیه 1.3(شرایط افراطی ضروری).
اجازه دهید تابع z =z(x,y),(x,y)D . نقطه م 0 (ایکس 0 ;y 0 دی - نقطه افراطی موضعی
اگر در این مرحله وجود دارد z" ایکس و z" y ، سپس
اثبات هندسی "بدیهی" است. اگر در نقطه سی 0 در (شکل 1.4) برای رسم یک صفحه مماس، سپس "به طور طبیعی" به صورت افقی، یعنی در یک زاویه عبور می کند. 0° به محور اوه و به محور OU .
سپس، مطابق با معنای هندسی مشتقات جزئی (شکل 1.3):
که قرار بود ثابت شود
تعریف 1.12.
اگر در نقطه م 0 شرایط (1.41) برآورده می شود، سپس به آن نقطه ثابت تابع می گویند z (x,y) .
قضیه 1.4(شرایط کافی برای یک افراطی).
اجازه دهید z =z(x,y),(x,y)D که دارای مشتقات جزئی مرتبه دوم در برخی از همسایگی های نقطه است م 0 (ایکس 0 ، y 0 )D . و م 0 - نقطه ثابت (یعنی شرایط لازم (1.41) برقرار است). بیایید محاسبه کنیم:
در اثبات قضیه از مباحثی (فرمول تیلور برای توابع چند متغیر و نظریه اشکال درجه دوم) استفاده می شود که در این آموزش به آنها پرداخته نشده است.
مثال 1.13.
تا حد زیادی کاوش کنید:
تصمیم گیری
1. نقاط ثابت را با حل سیستم (1.41) بیابید:
یعنی چهار نقطه ثابت پیدا می شود. 2.
توسط قضیه 1.4 در یک نقطه حداقل است. و 
توسط قضیه 1.4 در نقطه
بیشترین. و
و نیازی نیست به دنبال چیزی باشید: در مقاله جداگانه ما، ما قبلاً همه چیز را آماده کرده ایم تا بتوانید آن را انجام دهید. حالا بیایید در مورد مشتقات جزئی صحبت کنیم.
برای دریافت خبرنامه های مفید و اخبار روز دانشجو به کانال تلگرام ما خوش آمدید.
تابع دو یا چند متغیر
قبل از صحبت در مورد مشتقات جزئی، باید به مفهوم تابعی از چندین متغیر بپردازیم که بدون آن هیچ نقطه ای در مشتق جزئی وجود ندارد. در مدرسه، ما عادت داریم با توابع یک متغیر سر و کار داشته باشیم:
ما مشتقات چنین توابعی را قبلا در نظر گرفتیم. نمودار تابع یک متغیر یک خط در یک صفحه است: یک خط مستقیم، یک سهمی، یک هذلولی و غیره.
اگر متغیر دیگری اضافه کنیم چه؟ شما تابعی مانند این دریافت می کنید:
این تابعی از دو متغیر مستقل است ایکسو y. نمودار چنین تابعی یک سطح در فضای سه بعدی است: یک کره، یک هیپربولوئید، یک پارابولوئید یا برخی اسب های کروی دیگر در خلاء. توابع مشتق جزئی zبرای x و y به ترتیب به صورت زیر نوشته می شود:
همچنین توابعی از سه یا چند متغیر وجود دارد. درست است، ترسیم نمودار چنین تابعی غیرممکن است: حداقل به فضای چهار بعدی نیاز دارد که نمی توان آن را به تصویر کشید.
مشتق جزئی مرتبه اول
قانون اصلی را به خاطر بسپار:
هنگام محاسبه مشتق جزئی با توجه به یکی از متغیرها، متغیر دوم به عنوان یک ثابت در نظر گرفته می شود. در غیر این صورت، قوانین محاسبه مشتق تغییر نمی کند.
یعنی مشتق جزئی اساساً با مشتق معمول تفاوتی ندارد. بنابراین، جدول مشتقات توابع ابتدایی و قوانین محاسبه مشتقات معمولی را در مقابل چشمان خود نگه دارید. بیایید به یک مثال نگاه کنیم تا کاملا روشن شود. فرض کنید می خواهید مشتقات جزئی مرتبه اول تابع زیر را محاسبه کنید:
ابتدا مشتق جزئی را نسبت به x می گیریم و y را به عنوان یک عدد معمولی در نظر می گیریم:
اکنون مشتق جزئی را با توجه به y در نظر می گیریم و x را ثابت می گیریم:
همانطور که می بینید، هیچ چیز پیچیده ای در این مورد وجود ندارد و موفقیت با مثال های پیچیده تر فقط در حد تمرین است.
مشتق جزئی مرتبه دوم
مشتق جزئی مرتبه دوم چیست؟ درست مثل اولی. برای یافتن مشتقات جزئی مرتبه دوم، فقط باید مشتق مشتق مرتبه اول را بگیرید. بیایید به مثال بالا برگردیم و مشتقات جزئی مرتبه دوم را محاسبه کنیم.
بر اساس بازی:
مشتقات جزئی مرتبه سوم و بالاتر در اصل محاسبه تفاوتی ندارند. بیایید قوانین را سازماندهی کنیم:
- هنگام تمایز با توجه به یک متغیر مستقل، دومی به عنوان یک ثابت در نظر گرفته می شود.
- مشتق مرتبه دوم مشتق مشتق مرتبه اول است. مرتبه سوم مشتق مشتق مرتبه دوم و غیره است.
مشتقات جزئی و دیفرانسیل کل یک تابع
یک سوال متداول در کارهای عملی یافتن دیفرانسیل کل یک تابع است. برای تابعی از چندین متغیر، دیفرانسیل کل به عنوان بخش خطی اصلی افزایش کوچک کل تابع با توجه به افزایش آرگومان ها تعریف می شود.
تعریف دست و پا گیر به نظر می رسد، اما با حروف همه چیز آسان تر است. مجموع دیفرانسیل مرتبه اول یک تابع متشکل از چندین متغیر به صورت زیر است:
با دانستن نحوه محاسبه مشتقات جزئی، محاسبه دیفرانسیل کل مشکلی ندارد.
مشتقات جزئی چندان موضوع بیهوده ای نیستند. به عنوان مثال، معادلات دیفرانسیل جزئی مرتبه دوم به طور گسترده برای توصیف ریاضی فرآیندهای فیزیکی واقعی استفاده می شود.
در اینجا ما فقط یک ایده کلی و سطحی از مشتقات جزئی مرتبه اول و دوم ارائه کرده ایم. آیا به این موضوع علاقه دارید یا سؤال خاصی دارید؟ آنها را در نظرات بپرسید و با کارشناسان خدمات دانشجویی حرفه ای تماس بگیرید تا در تحصیل خود کمک شایانی و سریع کنند. با ما با مشکل تنها نخواهید ماند!
اصل کلی یافتن مشتقات جزئی مرتبه دوم تابعی از سه متغیر مشابه اصل یافتن مشتقات جزئی مرتبه دوم تابعی از دو متغیر است.
برای یافتن مشتقات جزئی مرتبه دوم، ابتدا باید مشتقات جزئی مرتبه اول را بیابید یا در نماد دیگری:
نه مشتق جزئی از مرتبه دوم وجود دارد.
گروه اول مشتقات دوم با توجه به متغیرهای مشابه هستند:
یا - مشتق دوم با توجه به "x"؛
یا - مشتق دوم نسبت به «ی»؛
یا - مشتق دوم نسبت به «ز».
گروه دوم هستند مختلطمشتقات جزئی مرتبه دوم، شش مورد از آنها وجود دارد:
یا - مختلطمشتق "با x y"؛
یا - مختلطمشتق "توسط y x"؛
یا - مختلطمشتق "با x z"؛
یا - مختلطمشتق "po zet x"؛
یا - مختلطمشتق "با بازی z"؛
یا - مختلطمشتق "po z y".
همانطور که در مورد تابعی از دو متغیر، هنگام حل مسائل، می توان بر برابری های زیر مشتقات مرتبه دوم مخلوط تمرکز کرد:
توجه: به طور دقیق، همیشه اینطور نیست. برای برابری مشتقات مختلط، لازم است شرط تداوم آنها برآورده شود.
در هر صورت، چند نمونه از نحوه خواندن این رسوایی با صدای بلند:
- "دو ضربه دو بار در سال"؛
- "de two y po de zet مربع"؛
- "دو ضربه روی x روی z"؛
- ” د دو ی پو د ز پو د ی ” .
مثال 10
تمام مشتقات جزئی مرتبه اول و دوم را برای تابعی از سه متغیر بیابید:
.
تصمیم:ابتدا مشتقات جزئی مرتبه اول را پیدا می کنیم:
مشتق یافت شده را می گیریم
و آن را با "y" متمایز کنید:
مشتق یافت شده را می گیریم
و آن را با "x" متمایز کنید:
برابری انجام می شود. خوب
ما با جفت دوم مشتقات مخلوط سروکار داریم.
مشتق یافت شده را می گیریم
و آن را با "z" متمایز کنید:
مشتق یافت شده را می گیریم
و آن را با "x" متمایز کنید:
برابری انجام می شود. خوب
به همین ترتیب، ما با جفت سوم مشتقات مختلط سروکار داریم:
برابری انجام می شود. خوب
پس از انجام کار، می توان تضمین کرد که اولاً همه مشتقات جزئی مرتبه 1 را به درستی پیدا کرده ایم و ثانیاً مشتقات جزئی مرکب مرتبه 2 را نیز به درستی پیدا کرده ایم.
باقی مانده است که سه مشتق جزئی دیگر از مرتبه دوم پیدا کنید، در اینجا، برای جلوگیری از خطا، باید تا حد امکان تمرکز کنید:
آماده. باز هم، کار آنقدر سخت نیست که حجیم است. راه حل را می توان کوتاه کرد و از آن به عنوان برابری مشتقات جزئی مختلط یاد کرد، اما در این مورد هیچ تأییدی وجود نخواهد داشت. پس بهتر است وقت بگذارید و پیدا کنید همهمشتقات (علاوه بر این، ممکن است معلم مورد نیاز باشد)، یا در موارد شدید، پیش نویس را بررسی کنید.
مثال 11
تمام مشتقات جزئی مرتبه اول و دوم را برای تابعی از سه متغیر بیابید
.
این یک مثال برای خودتان است.
راه حل ها و پاسخ ها:
مثال 2:تصمیم:
مثال 4:تصمیم: اجازه دهید مشتقات جزئی مرتبه اول را پیدا کنیم.
ما دیفرانسیل کل مرتبه اول را تشکیل می دهیم:
مثال 6:تصمیم: م(1, -1, 0):
مثال 7:تصمیم: اجازه دهید مشتقات جزئی مرتبه اول را در نقطه محاسبه کنیمم(1, 1, 1):
مثال 9:تصمیم:
مثال 11:تصمیم: بیایید مشتقات جزئی مرتبه اول را پیدا کنیم:
بیایید مشتقات جزئی مرتبه دوم را پیدا کنیم:
.
انتگرال ها
8.1. انتگرال نامعین. نمونه های راه حل تفصیلی
بیایید مطالعه موضوع را شروع کنیم انتگرال نامعین"، و همچنین نمونه هایی از راه حل های ساده ترین (و نه کاملاً) انتگرال ها را با جزئیات تجزیه و تحلیل کنید. طبق معمول، ما خود را به حداقل نظریه ای که در کتاب های درسی متعدد وجود دارد محدود می کنیم، وظیفه ما این است که یاد بگیریم چگونه انتگرال ها را حل کنیم.
برای تسلط موفقیت آمیز به مطالب چه چیزهایی باید بدانید؟ برای مقابله با حساب انتگرال، باید بتوانید مشتقات را حداقل در سطح متوسط پیدا کنید. اگر چندین ده، یا بهتر، صد مشتق مستقل را پشت سر خود داشته باشید، تجربه اضافی نخواهد بود. حداقل، نباید با کار تمایز ساده ترین و رایج ترین توابع گیج شوید.
به نظر می رسد، اگر در مورد انتگرال در مقاله صحبت می کنیم، اصلاً مشتقات کجا هستند؟! و موضوع اینجاست. واقعیت این است که یافتن مشتقات و یافتن انتگرال های نامعین (تمایز و انتگرال) دو عمل معکوس متقابل هستند، مانند جمع / تفریق یا ضرب / تقسیم. بنابراین، بدون مهارت و نوعی تجربه در یافتن مشتقات، متأسفانه نمی توان بیشتر از این پیش رفت.
در این راستا به مواد روش شناختی زیر نیاز خواهیم داشت: جدول مشتقو جدول انتگرال ها.
دشواری مطالعه انتگرال های نامعین چیست؟ اگر در مشتقات به شدت 5 قانون تمایز، جدول مشتقات و الگوریتم اقدامات نسبتاً واضح وجود داشته باشد، در انتگرال ها همه چیز متفاوت است. ده ها روش و تکنیک ادغام وجود دارد. و اگر روش ادغام در ابتدا اشتباه انتخاب شده باشد (یعنی شما نمی دانید چگونه آن را حل کنید) ، انتگرال را می توان به معنای واقعی کلمه برای چند روز "خارج" کرد ، مانند یک ربوس واقعی که سعی می کند متوجه ترفندها و ترفندهای مختلف شود. . حتی برخی آن را دوست دارند.
به هر حال، ما اغلب از دانش آموزان (نه علوم انسانی) نظری مانند: "من هرگز علاقه ای به حل حد یا مشتق نداشته ام، اما انتگرال ها یک موضوع کاملاً متفاوت هستند، هیجان انگیز است، همیشه میل به این وجود دارد." کرک "یک انتگرال پیچیده". متوقف کردن. طنز سیاه بس است، بیایید به سراغ این انتگرال های بسیار نامعین برویم.
از آنجایی که راه های زیادی برای حل وجود دارد، پس قوری از کجا شروع به مطالعه انتگرال های نامعین می کند؟ در حساب انتگرال، به نظر ما، سه ستون یا نوعی «محور» وجود دارد که هر چیز دیگری حول آن می چرخد. اول از همه، شما باید درک خوبی از ساده ترین انتگرال ها داشته باشید (این مقاله).
سپس باید درس را با جزئیات کار کنید. این مهم ترین پذیرش است! شاید حتی مهم ترین مقاله از همه مقالات به انتگرال ها اختصاص داده شده باشد. و سوم اینکه حتما بخوانید یکپارچه سازی توسط قطعات، زیرا کلاس وسیعی از توابع را ادغام می کند. اگر حداقل به این سه درس تسلط داشته باشید، در حال حاضر "دو تا" وجود ندارد. شما را می توان به خاطر ندانستن بخشید انتگرال توابع مثلثاتی, انتگرال کسرها, انتگرال توابع گویا کسری, انتگرال توابع غیر منطقی (ریشه)، اما اگر در روش جایگزینی یا ادغام با روش قطعات "در یک گودال قرار بگیرید" بسیار بسیار بد خواهد بود.
بنابراین، بیایید ساده شروع کنیم. بیایید به جدول انتگرال ها نگاه کنیم. همانطور که در مشتقات، چندین قانون یکپارچه سازی و جدولی از انتگرال های برخی از توابع ابتدایی را مشاهده می کنیم. هر انتگرال جدولی (و در واقع هر انتگرال نامعین) شکل زیر را دارد:
بیایید مستقیماً به نماد و اصطلاحات بپردازیم:
- نماد یکپارچه
- تابع انتگرال (نوشته شده با حرف "s").
- نماد دیفرانسیل اینکه چه چیزی است، به زودی بررسی خواهیم کرد. نکته اصلی این است که هنگام نوشتن انتگرال و در حین حل، مهم است که این نماد را از دست ندهید. نقص قابل توجهی وجود خواهد داشت.
انتگرال یا "پر کردن" انتگرال است.
– ضد مشتقعملکرد.
– . نیازی به بارگذاری شدید عبارت نیست، مهمترین چیز در اینجا این است که در هر انتگرال نامعین، یک ثابت به پاسخ اضافه می شود.
حل یک انتگرال نامعین به معنای یافتن استمجموعه ای از توابع ضد مشتقاز انتگرال داده شده
بیایید دوباره به ورودی نگاه کنیم:
بیایید به جدول انتگرال ها نگاه کنیم.
چه اتفاقی می افتد؟ قسمت های چپ ما در حال چرخش هستندبه توابع دیگر: .
بیایید تعریف خود را ساده کنیم:
انتگرال نامعین را حل کنید - به این معنی است که آن را به یک تابع نامعین (تا یک ثابت) تبدیل کنید ، با استفاده از برخی قوانین، تکنیک ها و جدول.
برای مثال انتگرال جدول را در نظر بگیرید 
. چی شد؟ رکورد نمادین به مجموعه ای از توابع ضد مشتق تبدیل شده است.
همانطور که در مورد مشتقات، برای یادگیری نحوه یافتن انتگرال، نیازی به آگاهی از چیستی انتگرال یا تابع ضد مشتق از دیدگاه نظری نیست. فقط انجام دگرگونی ها طبق برخی قوانین رسمی کافی است. بنابراین، در مورد درک اینکه چرا انتگرال دقیقاً به آن تبدیل می شود اصلاً ضروری نیست. شما می توانید این و فرمول های دیگر را مسلم فرض کنید. همه از الکتریسیته استفاده می کنند، اما تعداد کمی از مردم به این فکر می کنند که چگونه الکترون ها در طول سیم ها حرکت می کنند.
از آنجایی که تمایز و ادغام عملیات متضاد هستند، برای هر پاد مشتق که به درستی یافت می شود، موارد زیر صادق است:
به عبارت دیگر، اگر پاسخ صحیح متمایز شد، باید انتگرال اصلی به دست آید.
بیایید به همان انتگرال جدول برگردیم .
بیایید صحت این فرمول را بررسی کنیم. مشتق سمت راست را می گیریم:
انتگرال اصلی است.
به هر حال، واضح تر شد که چرا یک ثابت همیشه به یک تابع اختصاص داده می شود. هنگام تمایز، یک ثابت همیشه به صفر تبدیل می شود.
انتگرال نامعین را حل کنیدیعنی پیدا کردن یک دسته از همهضد مشتقات، و نه یک تابع واحد. در مثال جدولی در نظر گرفته شده،،،، و غیره - همه این توابع راه حل انتگرال هستند. راه حل های بی نهایت زیادی وجود دارد، بنابراین آنها به طور خلاصه می نویسند:
بنابراین، بررسی هر انتگرال نامعین به اندازه کافی آسان است. این مقداری جبران برای تعداد زیادی انتگرال از انواع مختلف است.
بیایید به مثال های خاص برویم. بیایید مانند مطالعه مشتق، با دو قانون ادغام شروع کنیم:
- مقدار ثابت سیمی توان (و باید) از علامت انتگرال خارج شود.
– انتگرال مجموع (تفاوت) دو تابع برابر است با مجموع (تفاوت) دو انتگرال. این قانون برای هر تعداد اصطلاح معتبر است.
همانطور که می بینید، قوانین اساساً مانند مشتقات است. گاهی اوقات آنها را صدا می زنند ویژگی های خطیانتگرال
مثال 1
انتگرال نامعین را پیدا کنید.
یک چک اجرا کنید.
تصمیم:راحت تر است که آن را مانند تبدیل کنید.
(1) اعمال قانون . فراموش نکنید که نماد دیفرانسیل را یادداشت کنید dxزیر هر انتگرال چرا زیر هر کدام؟ dxیک ضریب کامل است.اگر با جزئیات نقاشی می کنید، اولین مرحله باید به صورت زیر نوشته شود:
.
(2) طبق قاعده تمام ثوابت را از علائم انتگرال ها خارج می کنیم. توجه داشته باشید که در ترم گذشته tg 5 یک ثابت است، ما آن را نیز خارج می کنیم.
علاوه بر این، در این مرحله ریشه ها و درجات را برای ادغام آماده می کنیم. همانطور که در تمایز، ریشه ها باید در فرم نشان داده شوند . ریشه ها و درجاتی که در مخرج قرار دارند - به سمت بالا حرکت می کنند.
توجه داشته باشید:بر خلاف مشتقات، ریشه در انتگرال همیشه نیازی به کاهش به شکل نیست و درجه ها را به سمت بالا حرکت دهید.
مثلا، - این یک انتگرال جدولی آماده است که قبلاً محاسبه شده است و انواع ترفندهای چینی مانند کاملا غیر ضروری به همین ترتیب: - این نیز یک انتگرال جدولی است، هیچ فایده ای برای نشان دادن کسری در شکل وجود ندارد . جدول را با دقت مطالعه کنید!
(3) همه انتگرال ها جدولی هستند. ما تبدیل را با استفاده از جدول و با استفاده از فرمول ها انجام می دهیم: 
، و
برای یک تابع قدرت - 
.
لازم به ذکر است که انتگرال جدول یک مورد خاص از فرمول یک تابع توان است: 
.
مقدار ثابتسی فقط یک بار آن را در انتهای عبارت اضافه کنید
(به جای قرار دادن آنها بعد از هر انتگرال).
(4) ما نتیجه به دست آمده را در فرم فشرده تر، زمانی که تمام درجات فرم می نویسیم
دوباره به عنوان ریشه نشان داده می شود، و قدرت های دارای توان منفی به مخرج بازنشانی می شوند.
معاینه. برای انجام بررسی، باید پاسخ دریافتی را متمایز کنید:
اولیه یکپارچه، یعنی انتگرال به درستی پیدا شد. از آنچه رقصیدند، به آن بازگشتند. وقتی داستان با انتگرال همینطور تمام می شود خوب است.
گاه به گاه، رویکرد کمی متفاوت برای بررسی انتگرال نامعین وجود دارد، در حالی که مشتق نیست، بلکه دیفرانسیل از پاسخ گرفته می شود:
.
در نتیجه، ما نه یک انتگرال، بلکه یک انتگرال به دست می آوریم.
از مفهوم دیفرانسیل نترسید.
دیفرانسیل مشتق ضرب در است dx.
با این حال، این ظرافت های نظری نیست که برای ما مهم است، بلکه این است که در مرحله بعد با این تفاوت چه کنیم. دیفرانسیل به صورت زیر نشان داده می شود: نماد د حذف کنید، یک ضربه در سمت راست بالای براکت قرار دهید، یک ضریب در انتهای عبارت اختصاص دهید dx :
اصل دریافت کرد یکپارچهیعنی انتگرال به درستی پیدا می شود.
همانطور که می بینید، دیفرانسیل به یافتن مشتق می رسد. من روش دوم را برای بررسی کمتر دوست دارم، زیرا باید علاوه بر این باید براکت های بزرگ بکشم و نماد دیفرانسیل را بکشم. dx تا پایان آزمون اگر چه صحیح تر، یا «محکم تر» یا چیزی دیگر است.
در واقع می شد در مورد روش دوم راستی آزمایی سکوت کرد. نکته در روش نیست، بلکه در این است که ما یاد گرفته ایم دیفرانسیل را باز کنیم. از نو.
دیفرانسیل به صورت زیر آشکار می شود:
1) نماد دبرداشتن؛
2) یک سکته مغزی در سمت راست بالای براکت قرار دهید (تعریف مشتق).
3) در پایان عبارت یک فاکتور اختصاص می دهیم dx .
مثلا:
این را به خاطر بسپار. ما خیلی زود به تکنیک در نظر گرفته شده نیاز خواهیم داشت.
مثال 2
.
وقتی یک انتگرال نامعین پیدا می کنیم، همیشه سعی می کنیم بررسی کنیمعلاوه بر این، یک فرصت عالی برای این وجود دارد. همه انواع مسائل در ریاضیات عالی از این نظر هدیه نیستند. مهم نیست که تأیید اغلب در کارهای کنترلی مورد نیاز نیست، هیچ کس، و هیچ چیز مانع از انجام آن در یک پیش نویس نمی شود. فقط زمانی می توان استثنا قائل شد که زمان کافی وجود نداشته باشد (مثلاً در آزمون، امتحان). من شخصاً همیشه انتگرال ها را بررسی می کنم و عدم تأیید را یک هک و یک کار ضعیف می دانم.
مثال 3
انتگرال نامعین را پیدا کنید:
. یک چک اجرا کنید.
راه حل: با تجزیه و تحلیل انتگرال می بینیم که در زیر انتگرال حاصل ضرب دو تابع و حتی توان کل عبارت را داریم. متاسفانه در میدان نبرد انتگرال خیرخوب و راحت فرمول های ادغام محصول و ضریبمانند: 
یا 
.
بنابراین، هنگامی که یک محصول یا یک ضریب داده می شود، همیشه منطقی است که ببینیم آیا امکان تبدیل انتگرال به مجموع وجود دارد؟ مثال در نظر گرفته شده موردی است که ممکن است.
ابتدا راه حل کامل را می دهیم، نظرات در زیر خواهد بود.
(1) ما از فرمول خوب قدیمی برای مجذور مجموع برای هر اعداد واقعی استفاده می کنیم و از درجه بالای براکت مشترک خلاص می شویم. خارج از پرانتز و اعمال فرمول ضرب اختصاری در جهت مخالف: .
مثال 4
انتگرال نامعین را پیدا کنید
یک چک اجرا کنید.
این یک مثال برای حل خود است. پاسخ و حل کامل در پایان درس.
مثال 5
انتگرال نامعین را پیدا کنید
. یک چک اجرا کنید.
در این مثال، انتگرال یک کسری است. وقتی کسری را در انتگرال می بینیم، اولین فکر باید این سوال باشد: "آیا می توان به نحوی از شر این کسری خلاص شد یا حداقل آن را ساده کرد؟"
متوجه می‌شویم که مخرج دارای یک ریشه تنها از "x" است. یکی در میدان جنگجو نیست، به این معنی که می توانید صورت را به مخرج ترم تقسیم کنید:
ما در مورد اقدامات با قدرت کسری اظهار نظر نمی کنیم، زیرا آنها به طور مکرر در مقالات مربوط به مشتق یک تابع مورد بحث قرار گرفته اند.
اگر هنوز با چنین مثالی گیج می شوید
و هیچ کس جواب درستی نمی گیرد،
همچنین توجه داشته باشید که راه حل یک مرحله، یعنی اعمال قوانین را نادیده می گیرد , . معمولاً با تجربه خاصی در حل انتگرال ها، این قواعد یک واقعیت بدیهی تلقی می شوند و به تفصیل توضیح داده نمی شوند.
مثال 6
انتگرال نامعین را پیدا کنید. چک کنید
این یک مثال برای حل خود است. پاسخ و حل کامل در پایان درس.
در حالت کلی، با کسری در انتگرال، همه چیز چندان ساده نیست، مطالب اضافی در مورد ادغام کسرهای برخی از انواع را می توان در مقاله یافت: ادغام برخی کسرها. اما، قبل از رفتن به مقاله بالا، باید این درس را بخوانید: روش جایگزینی در انتگرال نامعین. واقعیت این است که جمع کردن یک تابع تحت یک روش تغییر دیفرانسیل یا متغیر است نقطه کلیدیدر مطالعه موضوع، زیرا نه تنها "در تکالیف خالص برای روش جایگزینی"، بلکه در بسیاری از انواع دیگر انتگرال ها نیز رخ می دهد.
راه حل ها و پاسخ ها:
مثال 2: راه حل:
مثال 4: راه حل:
در این مثال از فرمول ضرب کاهش یافته استفاده کردیم
مثال 6: راه حل:
روش تغییر متغیر در یک انتگرال نامعین. نمونه های راه حل
در این درس با یکی از مهم ترین و رایج ترین ترفندهایی که در درس حل انتگرال نامعین استفاده می شود – تغییر روش متغیر – آشنا می شویم. برای تسلط موفق بر مطالب، دانش اولیه و مهارت های یکپارچه سازی مورد نیاز است. اگر در حساب انتگرال احساس یک قوری پر خالی وجود دارد، ابتدا باید با مواد آشنا شوید. انتگرال نامعین. نمونه های راه حل، جایی که به شکلی در دسترس توضیح داده شده است که انتگرال چیست و نمونه های اساسی برای مبتدیان به تفصیل تجزیه و تحلیل می شوند.
از نظر فنی، روش تغییر یک متغیر در یک انتگرال نامعین به دو صورت اجرا می شود:
– قرار دادن تابع زیر علامت دیفرانسیل.
- تغییر واقعی متغیر.
در واقع، این یک چیز است، اما طراحی راه حل متفاوت به نظر می رسد. بیایید با یک مورد ساده تر شروع کنیم.
بارگذاری...
