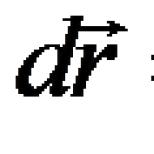وابستگی خطی اساس سیستم بردارها. وابستگی خطی و استقلال خطی بردارها. اساس بردارها. سیستم مختصات Affine با توجه به یک سیستم محدود از بردارها را پیدا کنید

در مقاله بردارهای n بعدی، به مفهوم فضای خطی تولید شده توسط مجموعه ای از بردارهای n بعدی رسیدیم. حال باید مفاهیم کم اهمیتی مانند بعد و اساس یک فضای برداری را در نظر بگیریم. آنها به طور مستقیم با مفهوم یک سیستم مستقل خطی از بردارها مرتبط هستند، بنابراین توصیه می شود که اصول این مبحث را نیز به خود یادآوری کنید.

اجازه دهید چند تعاریف را معرفی کنیم.

تعریف 1

ابعاد فضای برداریتعداد مربوط به حداکثر تعداد بردارهای مستقل خطی در این فضا است.

تعریف 2

مبنای فضای برداری- مجموعه ای از بردارهای مستقل خطی، مرتب شده و تعداد آنها برابر با بعد فضا است.

فضای مشخصی از n بردار را در نظر بگیرید. بعد آن به ترتیب برابر n است. بیایید سیستمی از بردارهای n واحدی را در نظر بگیریم:

e (1) = (1، 0، ...

بیایید از این بردارها به عنوان اجزای ماتریس A استفاده کنیم: واحدی با ابعاد n در n خواهد بود. رتبه این ماتریس n است. بنابراین، سیستم برداری e (1) , e (2) , . . . ، e (n) مستقل خطی است. در این حالت، اضافه کردن یک بردار به سیستم بدون نقض استقلال خطی آن غیرممکن است.

از آنجایی که تعداد بردارهای سیستم برابر با n است، پس بعد فضای بردارهای n بعدی برابر با n و بردارهای واحد e (1) , e (2) , . . . ، e (n) اساس فضای مشخص شده هستند.

از تعریف به دست آمده نتیجه می گیریم: هر سیستمی از بردارهای n بعدی که در آن تعداد بردارها کمتر از n باشد، مبنای فضا نیست.

اگر بردار اول و دوم را مبادله کنیم، سیستمی از بردارهای e (2) , e (1) , . . . ، e (n) . همچنین مبنای یک فضای برداری n بعدی خواهد بود. اجازه دهید یک ماتریس بسازیم و بردارهای سیستم حاصل را به عنوان ردیف آن در نظر بگیریم. ماتریس را می توان از ماتریس هویت با جابجایی دو ردیف اول بدست آورد، رتبه آن برابر با n خواهد بود. سیستم e (2) , e (1) , . . . ، e (n) مستقل خطی است و مبنای یک فضای برداری n بعدی است.

با مرتب کردن مجدد سایر بردارها در سیستم اصلی، یک پایه دیگر دریافت می کنیم.

ما می‌توانیم یک سیستم مستقل خطی از بردارهای غیر واحدی بگیریم، و این نیز مبنای یک فضای برداری n بعدی را نشان می‌دهد.

تعریف 3

فضای برداری با بعد n به تعداد سیستم های مستقل خطی از بردارهای n بعدی با عدد n پایه دارد.

هواپیما یک فضای دو بعدی است - اساس آن هر دو بردار غیر خطی خواهد بود. هر سه بردار غیرهمسطح به عنوان مبنای فضای سه بعدی عمل می کنند.

کاربرد این نظریه را در نمونه های خاص در نظر بگیرید.

مثال 1

اطلاعات اولیه:بردارها

a = (3، - 2، 1) b = (2، 1، 2) c = (3، - 1، - 2)

باید مشخص شود که آیا بردارهای مشخص شده اساس یک فضای برداری سه بعدی هستند یا خیر.

تصمیم گیری

برای حل مسئله، سیستم بردارهای داده شده را برای یک وابستگی خطی مطالعه می کنیم. بیایید یک ماتریس بسازیم که در آن سطرها مختصات بردارها هستند. اجازه دهید رتبه ماتریس را تعیین کنیم.

A = 3 2 3 - 2 1 - 1 1 2 - 2 A = 3 - 2 1 2 1 2 3 - 1 - 2 = 3 1 (- 2) + (- 2) 2 3 + 1 2 (- 1) - 1 1 3 - (- 2) 2 (- 2) - 3 2 (- 1) = = - 25 ≠ 0 ⇒ R a n k (A) = 3

در نتیجه، بردارهای داده شده توسط شرط مسئله به صورت خطی مستقل هستند و تعداد آنها برابر با بعد فضای برداری است - آنها اساس فضای برداری هستند.

پاسخ:این بردارها اساس فضای برداری هستند.

مثال 2

اطلاعات اولیه:بردارها

a = (3، - 2، 1) b = (2، 1، 2) c = (3، - 1، - 2) d = (0، 1، 2)

باید مشخص شود که آیا سیستم بردارهای مشخص شده می تواند مبنای یک فضای سه بعدی باشد یا خیر.

تصمیم گیری

سیستم بردارهای مشخص شده در شرایط مسئله به صورت خطی وابسته است، زیرا حداکثر تعداد بردارهای مستقل خطی 3 است. بنابراین، این سیستم از بردارها نمی تواند به عنوان مبنایی برای فضای برداری سه بعدی باشد. اما شایان ذکر است که زیرسیستم سیستم اصلی a = (3 , - 2 , 1) , b = (2 , 1 , 2) , c = (3 , - 1 , - 2) مبنا است.

پاسخ:سیستم بردارهای مشخص شده مبنایی نیست.

مثال 3

اطلاعات اولیه:بردارها

a = (1، 2، 3، 3) b = (2، 5، 6، 8) c = (1، 3، 2، 4) d = (2، 5، 4، 7)

آیا می توانند مبنای یک فضای چهار بعدی باشند؟

تصمیم گیری

با استفاده از مختصات بردارهای داده شده به عنوان ردیف، یک ماتریس بسازید

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

با استفاده از روش گاوس، رتبه ماتریس را تعیین می کنیم:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7 ~ 1 2 3 3 0 1 0 2 0 1 - 1 1 0 1 - 2 1 ~ ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 - 2 - 1 ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 0 1 ⇒ ⇒ R a n k (A) = 4

بنابراین، سیستم بردارهای داده شده به صورت خطی مستقل است و تعداد آنها برابر با بعد فضای برداری است - آنها اساس فضای برداری چهار بعدی هستند.

پاسخ:بردارهای داده شده اساس فضای چهار بعدی هستند.

مثال 4

اطلاعات اولیه:بردارها

a (1) = (1، 2، - 1، - 2) a (2) = (0، 2، 1، - 3) a (3) = (1، 0، 0، 5)

آیا آنها اساس یک فضای 4 بعدی را تشکیل می دهند؟

تصمیم گیری

سیستم اصلی بردارها به صورت خطی مستقل است، اما تعداد بردارهای موجود در آن برای تبدیل شدن به مبنای یک فضای چهار بعدی کافی نیست.

پاسخ:نه، آنها نمی کنند.

تجزیه یک بردار بر حسب مبنا

ما قبول داریم که بردارهای دلخواه e (1) , e (2) , . . . ، e (n) اساس یک فضای بردار n بعدی هستند. بیایید مقداری بردار n بعدی x → به آنها اضافه کنیم: سیستم بردارها به صورت خطی وابسته خواهد شد. ویژگی های وابستگی خطی بیان می کند که حداقل یکی از بردارهای چنین سیستمی را می توان به صورت خطی بر حسب بردارهای دیگر بیان کرد. با فرمول‌بندی مجدد این عبارت، می‌توان گفت که حداقل یکی از بردارهای یک سیستم وابسته خطی را می‌توان بر حسب سایر بردارها گسترش داد.

بنابراین، ما به فرمول بندی مهمترین قضیه رسیدیم:

تعریف 4

هر بردار فضای برداری n بعدی به طور منحصر به فردی بر حسب یک مبنا تجزیه می شود.

اثبات 1

بیایید این قضیه را ثابت کنیم:

پایه فضای برداری n بعدی را تنظیم کنید - e (1), e (2) , . . . ، e (n) . بیایید سیستم را با افزودن یک بردار n بعدی x → به آن وابسته خطی کنیم. این بردار را می توان به صورت خطی بر حسب بردارهای اصلی بیان کرد:

x = x 1 e (1) + x 2 e (2) + . . . + x n e (n)، که در آن x 1، x 2، . . . ، x n - تعدادی اعداد.

اکنون ثابت می کنیم که چنین تجزیه ای منحصر به فرد است. فرض کنید که اینطور نیست و بسط مشابه دیگری وجود دارد:

x = x ~ 1 e (1) + x 2 ~ e (2) + . . . + x ~ n e (n)، که در آن x ~ 1، x ~ 2، . . . , x ~ n - برخی از اعداد.

از قسمت چپ و راست این تساوی به ترتیب قسمت چپ و راست تساوی را کم کنید x = x 1 · e (1) + x 2 · e (2) + . . . + x n e (n) . ما گرفتیم:

0 = (x ~ 1 - x 1) e (1) + (x ~ 2 - x 2) e (2) + . . . (x~n - xn) e(2)

سیستم بردارهای پایه e (1) , e (2) , . . . ، e (n) مستقل خطی است. با تعریف استقلال خطی یک سیستم از بردارها، تساوی فوق تنها زمانی امکان پذیر است که همه ضرایب (x ~ 1 - x 1) , (x ~ 2 - x 2) باشند. . . ، (x ~ n - x n) برابر با صفر خواهد بود. که از آن منصفانه خواهد بود: x 1 \u003d x ~ 1، x 2 \u003d x ~ 2،. . . , x n = x ~ n . و این تنها راه را برای گسترش یک بردار از نظر مبنا ثابت می کند.

در این حالت ضرایب x 1 , x 2 , . . . , x n مختصات بردار x → در پایه e (1) , e (2) , . . . ، e (n) .

نظریه اثبات شده عبارت "بردار n بعدی x = (x 1 , x 2 , . . . , x n) داده شده است" را روشن می کند: یک فضای برداری x → n بعدی در نظر گرفته می شود و مختصات آن در برخی از پایه ها همچنین واضح است که همان بردار در مبنای متفاوتی از فضای n بعدی مختصات متفاوتی خواهد داشت.

مثال زیر را در نظر بگیرید: فرض کنید در برخی از پایه های یک فضای برداری n بعدی، سیستمی از n بردار مستقل خطی داده می شود.

و همچنین بردار x = (x 1 , x 2 , . . . , x n ) داده شده است.

بردارهای e 1 (1) , e 2 (2) , . . . ، e n (n) در این مورد نیز اساس این فضای برداری هستند.

فرض کنید که لازم است مختصات بردار x → در مبنای e 1 (1) , e 2 (2) , , تعیین شود. . . , e n (n) , با x ~ 1 , x ~ 2 , نشان داده می شود. . . , x ~ n .

بردار x → به صورت زیر نمایش داده می شود:

x = x ~ 1 e (1) + x ~ 2 e (2) + . . . + x ~ n e(n)

این عبارت را به صورت مختصات می نویسیم:

(x 1 , x 2 , . . , x n) = x ~ 1 (e (1) 1 , e (1) 2 , . . . , e (1) n) + x ~ 2 (e (2 ) 1 , e (2) 2 , . . . , e (2) n) + . . . + + x ~ n (e (n) 1 , e (n) 2 , . . . , e (n) n) = = (x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + . . . + x ~ n e 1 (n) , x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + + . . + x ~ n e 2 (n) , . . , x ~ 1 e n (1) + x ~ 2 e n (2) + . . . + x ~ n e n (n))

برابری حاصل معادل سیستمی از n عبارت جبری خطی با n متغیر خطی مجهول x ~ 1 , x ~ 2 , است. . . , x ~ n:

x 1 = x ~ 1 e 1 1 + x ~ 2 e 1 2 + . . . + x ~ n e 1 n x 2 = x ~ 1 e 2 1 + x ~ 2 e 2 2 + . . . + x ~ n e 2 n ⋮ x n = x ~ 1 e n 1 + x ~ 2 e n 2 + . . . + x ~ n e n n

ماتریس این سیستم به شکل زیر خواهد بود:

e 1 (1) e 1 (2) ⋯ e 1 (n) e 2 (1) e 2 (2) ⋯ e 2 (n) ⋮ ⋮ ⋮ ⋮ e n (1) e n (2) ⋯ e n (n)

اجازه دهید این یک ماتریس A باشد و ستون های آن بردارهای یک سیستم مستقل خطی از بردارهای e 1 (1) , e 2 (2) , . . . , e n (n) . رتبه ماتریس n و تعیین کننده آن غیر صفر است. این نشان می دهد که سیستم معادلات یک راه حل منحصر به فرد دارد که می توان آن را به هر روشی مناسب تعیین کرد: به عنوان مثال، با روش کرامر یا با روش ماتریس. به این ترتیب می توانیم مختصات x ~ 1 , x ~ 2 , را تعیین کنیم. . . , x ~ n از بردار x → در پایه e 1 (1) , e 2 (2) , . . . , e n (n) .

بیایید نظریه در نظر گرفته شده را روی یک مثال عینی اعمال کنیم.

مثال 6

اطلاعات اولیه:بردارها بر اساس فضای سه بعدی آورده شده است

e (1) = (1، - 1، 1) e (2) = (3، 2، - 5) e (3) = (2، 1، - 3) x = (6، 2، - 7)

تأیید این واقعیت ضروری است که سیستم بردارهای e (1) ، e (2) ، e (3) نیز به عنوان مبنای فضای داده شده عمل می کند و همچنین مختصات بردار x را در مبنای داده شده تعیین می کند. .

تصمیم گیری

سیستم بردارهای e (1) , e (2) , e (3) اگر به صورت خطی مستقل باشد مبنای فضای سه بعدی خواهد بود. اجازه دهید با تعیین رتبه ماتریس A به این امکان پی ببریم که ردیف های آن بردارهای داده شده e (1) , e (2) , e (3) هستند.

ما از روش گاوس استفاده می کنیم:

A = 1 - 1 1 3 2 - 5 2 1 - 3 ~ 1 - 1 1 0 5 - 8 0 3 - 5 ~ 1 - 1 1 0 5 - 8 0 0 - 1 5

R a n k (A) = 3 . بنابراین، سیستم بردارهای e (1)، e (2)، e (3) به طور خطی مستقل است و یک مبنا است.

بگذارید بردار x → در پایه دارای مختصات x ~ 1 , x ~ 2 , x ~ 3 باشد. ارتباط این مختصات با معادله تعیین می شود:

x 1 = x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + x ~ 3 e 1 (3) x 2 = x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + x ~ 3 e 2 (3) x 3 = x ~ 1 e 3 (1) + x ~ 2 e 3 (2) + x ~ 3 e 3 (3)

بیایید مقادیر را با توجه به شرایط مسئله اعمال کنیم:

x ~ 1 + 3 x ~ 2 + 2 x ~ 3 = 6 - x ~ 1 + 2 x ~ 2 + x ~ 3 = 2 x ~ 1 - 5 x ~ 2 - 3 x 3 = - 7

ما سیستم معادلات را با روش کرامر حل می کنیم:

∆ = 1 3 2 - 1 2 1 1 - 5 - 3 = - 1 ∆ x ~ 1 = 6 3 2 2 2 1 - 7 - 5 - 3 = - 1 , x ~ 1 = ∆ x ~ 1 ∆ = - 1 - 1 = 1 ∆ x ~ 2 = 1 6 2 - 1 2 1 1 - 7 - 3 = - 1 ، x ~ 2 = ∆ x ~ 2 ∆ = - 1 - 1 = 1 ∆ x ~ 3 = 1 3 6 - 1 2 2 1 - 5 - 7 = - 1 ، x ~ 3 = ∆ x ~ 3 ∆ = - 1 - 1 = 1

بنابراین، بردار x → در پایه e (1)، e (2)، e (3) دارای مختصات x ~ 1 = 1، x ~ 2 = 1، x ~ 3 = 1 است.

پاسخ: x = (1، 1، 1)

اتصال بین پایه ها

فرض کنید در برخی از پایه های یک فضای برداری n بعدی، دو سیستم مستقل خطی از بردارها آورده شده است:

c (1) = (c 1 (1) , c 2 (1) , . . . , c n (1)) c (2) = (c 1 (2) , c 2 (2) , . . . , c n (2)) ⋮ c (n) = (c 1 (n) , e 2 (n) , . . . , c n (n))

e (1) = (e 1 (1) , e 2 (1) , . . . , e n (1)) e (2) = (e 1 (2) , e 2 (2) , . . . , e n (2)) ⋮ e (n) = (e 1 (n) , e 2 (n) , . . . , e n (n))

این سیستم ها نیز پایه های فضای داده شده هستند.

بگذارید c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1) - مختصات بردار c (1) در پایه e (1) , e (2) , . . . ، e (3) ، سپس رابطه مختصات توسط یک سیستم معادلات خطی داده می شود:

c 1 (1) = c ~ 1 (1) e 1 (1) + c ~ 2 (1) e 1 (2) + . . . + c ~ n (1) e 1 (n) c 2 (1) = c ~ 1 (1) e 2 (1) + c ~ 2 (1) e 2 (2) + . . . + c ~ n (1) e 2 (n) ⋮ c n (1) = c ~ 1 (1) e n (1) + c ~ 2 (1) e n (2) + . . . + c ~ n (1) e n (n)

در قالب یک ماتریس، سیستم را می توان به صورت زیر نمایش داد:

ج 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

بیایید همان نماد را برای بردار c (2) با قیاس ایجاد کنیم:

ج 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

ج 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

برابری های ماتریسی در یک عبارت ترکیب می شوند:

c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n) = c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n)

رابطه بردارهای دو پایه مختلف را تعیین می کند.

با استفاده از همین اصل، می توان تمام بردارهای پایه e (1) , e (2) , . . . , e (3) از طریق پایه c (1) , c (2) , . . . , c (n) :

e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n) = e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n)

ما تعاریف زیر را ارائه می دهیم:

تعریف 5

ماتریس c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) ماتریس گذار از پایه e (1) , e (2) , . . . , e (3)

به پایه c (1) , c (2) , . . . ، ج (ن) .

تعریف 6

ماتریس e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) ماتریس گذار از پایه c (1) , c (2) , . . . ,c(n)

به اساس e (1) , e (2) , . . . ، ه (3) .

از این برابری ها معلوم می شود که

c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 e ~ 1 ~ 2 (1) e ) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1

آن ها ماتریس های انتقال متقابل معکوس هستند.

بیایید نظریه را بر روی یک مثال عینی در نظر بگیریم.

مثال 7

اطلاعات اولیه:لازم است ماتریس انتقال را از پایه پیدا کنیم

c (1) = (1، 2، 1) c (2) = (2، 3، 3) c (3) = (3، 7، 1)

e (1) = (3، 1، 4) e (2) = (5، 2، 1) e (3) = (1، 1، - 6)

همچنین باید رابطه مختصات یک بردار دلخواه x → را در پایه های داده شده مشخص کنید.

تصمیم گیری

1. اجازه دهید T ماتریس انتقال باشد، سپس برابری درست خواهد بود:

3 1 4 5 2 1 1 1 1 = T 1 2 1 2 3 3 3 7 1

دو طرف معادله را در ضرب کنید

1 2 1 2 3 3 3 7 1 - 1

و دریافت کنید:

T = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1

2. ماتریس انتقال را تعریف کنید:

T = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1 = = 3 1 4 5 2 1 1 1 - 6 - 18 5 3 7 - 2 - 1 5 - 1 - 1 = - 27 9 4 - 71 20 12 - 41 9 8

3. رابطه مختصات بردار x → را تعریف کنید:

فرض کنید که در مبنای c (1) , c (2) , . . . , c (n) بردار x → دارای مختصات x 1 , x 2 , x 3 است، سپس:

x \u003d (x 1، x 2، x 3) 1 2 1 2 3 3 7 1،

و در مبنای e (1) , e (2) , . . . ، e (3) دارای مختصات x ~ 1، x ~ 2، x ~ 3 است، سپس:

x = (x ~ 1، x ~ 2، x ~ 3) 3 1 4 5 2 1 1 1 - 6

زیرا قسمت‌های چپ این تساوی‌ها با هم برابر هستند، می‌توانیم قسمت‌های سمت راست را نیز برابر کنیم:

(x 1 , x 2 , x 3) 1 2 1 2 3 3 7 1 = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 - 6

هر دو طرف سمت راست را در ضرب کنید

1 2 1 2 3 3 3 7 1 - 1

و دریافت کنید:

(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1 ⇔ ⇔ ( x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) T ⇔ ⇔ (x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3 ) - 27 9 4 - 71 20 12 - 41 9 8

از طرف دیگر

(x ~ 1، x ~ 2، x ~ 3) = (x 1، x 2، x 3) - 27 9 4 - 71 20 12 - 41 9 8

آخرین برابری ها رابطه مختصات بردار x → را در هر دو پایه نشان می دهد.

پاسخ:ماتریس انتقال

27 9 4 - 71 20 12 - 41 9 8

مختصات بردار x → در پایه های داده شده با رابطه زیر مرتبط می شوند:

(x 1، x 2، x 3) = (x ~ 1، x ~ 2، x ~ 3) - 27 9 4 - 71 20 12 - 41 9 8

(x ~ 1، x ~ 2، x ~ 3) = (x 1، x 2، x 3) - 27 9 4 - 71 20 12 - 41 9 8 - 1

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

وابستگی خطی و استقلال خطی بردارها.
اساس بردارها. سیستم مختصات افین

یک گاری با شکلات در بین مخاطبان وجود دارد و امروز هر بازدیدکننده یک زوج شیرین - هندسه تحلیلی با جبر خطی - دریافت می کند. در این مقاله به طور همزمان به دو بخش از ریاضیات عالی پرداخته خواهد شد و خواهیم دید که چگونه آنها در یک بسته بندی کنار می آیند. استراحت کن، توئیکس بخور! ... لعنتی، خب، بحث مزخرف. اگرچه خوب است، من گل نمی زنم، اما در نهایت باید نگرش مثبتی برای مطالعه وجود داشته باشد.

وابستگی خطی بردارها, استقلال خطی بردارها, مبنای برداریو اصطلاحات دیگر نه تنها تفسیر هندسی دارند، بلکه بیش از همه معنای جبری دارند. خود مفهوم "بردار" از دیدگاه جبر خطی از همیشه بردار "معمولی" است که ما می توانیم در یک صفحه یا در فضا به تصویر بکشیم. برای اثبات نیازی به جستجوی دور ندارید، سعی کنید بردار فضای پنج بعدی را ترسیم کنید . یا بردار آب و هوا که من فقط به Gismeteo رفتم به ترتیب: - دما و فشار اتمسفر. مثال، البته، از نقطه نظر ویژگی های فضای برداری نادرست است، اما، با این وجود، هیچ کس رسمی کردن این پارامترها را به عنوان یک بردار ممنوع نمی کند. نفس پاییزی...

نه، من شما را با تئوری خسته نمی کنم، فضاهای برداری خطی، وظیفه این است که فهمیدنتعاریف و قضایا اصطلاحات جدید (وابستگی خطی، استقلال، ترکیب خطی، مبنا و ...) برای همه بردارها از نظر جبری قابل استفاده است، اما مثال هایی به صورت هندسی ارائه خواهد شد. بنابراین، همه چیز ساده، در دسترس و بصری است. علاوه بر مسائل هندسه تحلیلی، برخی از وظایف معمول جبر را نیز در نظر خواهیم گرفت. برای تسلط بر مطالب، توصیه می شود با دروس آشنا شوید وکتور برای آدمکو چگونه تعیین کننده را محاسبه کنیم؟

وابستگی و استقلال خطی بردارهای صفحه.
اساس صفحه و سیستم مختصات افین

صفحه میز کامپیوتر خود را در نظر بگیرید (فقط یک میز، میز کنار تخت، کف، سقف، هر چیزی که دوست دارید). وظیفه شامل اقدامات زیر خواهد بود:

1) پایه هواپیما را انتخاب کنید. به طور کلی، میز یک طول و عرض دارد، بنابراین به طور مستقیم واضح است که دو بردار برای ساختن پایه مورد نیاز است. واضح است که یک بردار کافی نیست، سه بردار زیاد است.

2) بر اساس مبنای انتخاب شده تنظیم سیستم مختصات(شبکه مختصات) برای اختصاص مختصات به همه موارد روی میز.

تعجب نکنید، در ابتدا توضیحات روی انگشتان خواهد بود. علاوه بر این، در مورد شما. لطفا قرار دهید انگشت اشاره دست چپروی لبه میز به طوری که او به مانیتور نگاه می کند. این یک بردار خواهد بود. اکنون قرار دهید انگشت کوچک دست راستروی لبه میز به همین ترتیب - به طوری که به صفحه نمایشگر هدایت شود. این یک بردار خواهد بود. لبخند بزنید، عالی به نظر می رسید! در مورد بردارها چه می توان گفت؟ بردارهای داده خطی، که به معنی به صورت خطیاز طریق یکدیگر بیان می شود:
، خوب، یا برعکس: ، جایی که یک عدد غیر صفر است.

تصویری از این عمل را در درس مشاهده می کنید. وکتور برای آدمک، جایی که قانون ضرب بردار در عدد را توضیح دادم.

آیا انگشتان شما اساس صفحه میز کامپیوتر را تعیین می کنند؟ بدیهی است که نه. بردارهای خطی به سمت جلو و عقب حرکت می کنند تنهاجهت، در حالی که یک هواپیما دارای طول و عرض است.

چنین بردارهایی نامیده می شوند وابسته به خط.

ارجاع: کلمات "خطی"، "خطی" بیانگر این واقعیت است که در معادلات، عبارات ریاضی، مربع، مکعب، توان های دیگر، لگاریتم، سینوس و غیره وجود ندارد. فقط عبارات و وابستگی های خطی (درجه 1) وجود دارد.

دو بردار صفحه وابسته به خطاگر و فقط در صورتی که هم خط باشند.

انگشتان خود را روی میز روی میز قرار دهید تا هر زاویه ای بین آنها وجود داشته باشد به جز 0 یا 180 درجه. دو بردار صفحهبه صورت خطی نهوابستگی دارند اگر و فقط اگر هم خط نباشند. بنابراین، اساس دریافت می شود. لازم نیست خجالت بکشید که پایه با بردارهای غیر عمود با طول های مختلف "مورب" است. به زودی خواهیم دید که نه تنها زاویه 90 درجه برای ساخت آن مناسب است و نه تنها بردارهای واحد با طول مساوی.

هربردار هواپیما تنها راهاز نظر پایه گسترش یافته است:
، اعداد واقعی کجا هستند. اعداد نامیده می شوند مختصات برداریدر این مبنا

این را هم می گویند برداردر فرم ارائه شده است ترکیب خطیبردارهای پایه. یعنی بیان نامیده می شود تجزیه برداریاساسیا ترکیب خطیبردارهای پایه

به عنوان مثال، می توان گفت که یک بردار در یک پایه متعامد از صفحه منبسط شده است، یا می توان گفت که به صورت ترکیبی خطی از بردارها نشان داده شده است.

فرمول بندی کنیم تعریف پایهبه طور رسمی: پایه هواپیمایک جفت بردار مستقل خطی (غیر خطی) است، ، که در آن هربردار صفحه ترکیبی خطی از بردارهای پایه است.

نکته اساسی در تعریف این واقعیت است که بردارها گرفته شده اند به ترتیب خاصی. پایه ها این دو پایه کاملا متفاوت هستند! همانطور که می گویند انگشت کوچک دست چپ را نمی توان به جای انگشت کوچک دست راست برد.

ما اساس را فهمیدیم، اما تنظیم شبکه مختصات و اختصاص مختصات به هر آیتم روی میز کامپیوتر شما کافی نیست. چرا کافی نیست؟ بردارها آزاد هستند و در کل صفحه سرگردان هستند. پس چگونه مختصات را به آن نقاط کوچک جدول کثیف باقی مانده از یک آخر هفته وحشی اختصاص دهید؟ یک نقطه شروع مورد نیاز است. و چنین نقطه مرجعی برای همه آشناست - مبدأ مختصات. آشنایی با سیستم مختصات:

من با سیستم "مدرسه" شروع می کنم. در حال حاضر در درس مقدماتی وکتور برای آدمکمن برخی از تفاوت‌های بین یک سیستم مختصات مستطیلی و یک پایه متعارف را برجسته کردم. این هم تصویر استاندارد:

هنگام صحبت در مورد سیستم مختصات مستطیلی، سپس اغلب آنها به معنای مبدا، محورهای مختصات و مقیاس در امتداد محورها هستند. سعی کنید "سیستم مختصات مستطیلی" را در موتور جستجو تایپ کنید، خواهید دید که بسیاری از منابع در مورد محورهای مختصات آشنا از کلاس پنجم تا ششم و نحوه ترسیم نقاط در هواپیما به شما می گویند.

از سوی دیگر، این تصور به وجود می‌آید که یک سیستم مختصات مستطیلی را می‌توان به‌خوبی بر اساس یک مبنای متعارف تعریف کرد. و تقریباً همینطور است. جمله بندی به این صورت است:

اصل و نسب، و متعارفمجموعه پایه سیستم مختصات دکارتی هواپیما . یعنی یک سیستم مختصات مستطیلی شکل قطعابا یک نقطه و دو بردار متعامد واحد تعریف می شود. به همین دلیل است که نقشه ای را که در بالا ارائه کردم مشاهده می کنید - در مسائل هندسی، هم بردارها و هم محورهای مختصات اغلب (اما دور از همیشه) ترسیم می شوند.

فکر می کنم همه با کمک یک نقطه (منشا) و یک مبنای متعارف آن را درک می کنند هر نقطه از هواپیما و هر بردار هواپیمامختصات را می توان اختصاص داد. به بیان تصویری، "همه چیز در هواپیما را می توان شماره گذاری کرد."

آیا بردارهای مختصات باید واحد باشند؟ نه، آنها می توانند یک طول دلخواه غیر صفر داشته باشند. یک نقطه و دو بردار متعامد با طول دلخواه غیر صفر را در نظر بگیرید:

چنین مبنایی نامیده می شود ارتودنسی. مبدأ مختصات با بردارها شبکه مختصات را مشخص می کند و هر نقطه از صفحه، هر بردار مختصات خود را در مبنای داده شده دارد. به عنوان مثال، یا. ناراحتی آشکار این است که بردارهای مختصات به طور کلیطول های متفاوتی غیر از وحدت دارند. اگر طول ها برابر با یک باشند، مبنای معمول متعارف به دست می آید.

! توجه داشته باشید : در پایه متعامد و همچنین در زیر در پایه های افین صفحه و فضا واحدهایی در امتداد محورها در نظر گرفته می شود. مشروط. به عنوان مثال، یک واحد در امتداد آبسیسا شامل 4 سانتی‌متر، یک واحد در امتداد مختصات حاوی 2 سانتی‌متر است. این اطلاعات برای تبدیل مختصات «غیر استاندارد» به «سانتی‌مترهای معمول» در صورت لزوم کافی است.

و سوال دوم که در واقع قبلاً پاسخ داده شده است - آیا لازم است زاویه بین بردارهای پایه برابر با 90 درجه باشد؟ نه! همانطور که تعریف می گوید، بردارهای پایه باید باشند فقط غیر خطی. بر این اساس، زاویه می تواند هر چیزی به جز 0 و 180 درجه باشد.

یک نقطه در هواپیما به نام اصل و نسب، و غیر خطیبردارها ، تنظیم سیستم مختصات وابسته هواپیما :

گاهی اوقات این سیستم مختصات نامیده می شود موربسیستم. نقاط و بردارها به عنوان نمونه در نقاشی نشان داده شده اند:

همانطور که می دانید، سیستم مختصات affine حتی کمتر راحت است، فرمول های طول بردارها و بخش ها، که در قسمت دوم درس در نظر گرفتیم، در آن کار نمی کنند. وکتور برای آدمک، بسیاری از فرمول های خوشمزه مربوط به حاصل ضرب اسکالر بردارها. اما قوانین جمع بردارها و ضرب یک بردار در یک عدد معتبر است، فرمول های تقسیم یک بخش از این نظر و همچنین برخی از انواع دیگر مسائل که به زودی بررسی خواهیم کرد.

و نتیجه این است که راحت‌ترین مورد خاص از یک سیستم مختصات افین، سیستم مستطیلی دکارتی است. بنابراین، او، خودش، اغلب باید دیده شود. ... با این حال، همه چیز در این زندگی نسبی است - موقعیت های زیادی وجود دارد که در آنها مناسب است یک مورب (یا موارد دیگر، برای مثال، قطبی) دستگاه مختصات. بله، و انسان نماها ممکن است چنین سیستم هایی را بچشند =)

بیایید به بخش عملی آن برویم. تمام مشکلات این درس هم برای یک سیستم مختصات مستطیلی و هم برای حالت کلی آفین معتبر است. در اینجا هیچ چیز پیچیده ای وجود ندارد، تمام مطالب حتی برای یک دانش آموز در دسترس است.

چگونه می توان هم خطی بردارهای صفحه را تعیین کرد؟

چیز معمولی به منظور دو بردار صفحه خطی هستند، لازم و کافی است که مختصات مربوطه آنها متناسب باشداساساً، این یک اصلاح مختص به مختصات از رابطه آشکار است.

مثال 1

الف) بررسی کنید که آیا بردارها خطی هستند یا خیر .
ب) آیا بردارها مبنایی را تشکیل می دهند؟ ?

تصمیم:
الف) بررسی کنید که آیا برای بردارها وجود دارد یا خیر ضریب تناسب، به طوری که برابری برآورده شود:

من قطعاً در مورد نسخه "foppish" استفاده از این قانون به شما خواهم گفت که در عمل بسیار خوب عمل می کند. ایده این است که فوراً نسبتی را ترسیم کنید و ببینید درست است یا خیر:

بیایید نسبتی از نسبت مختصات مربوط به بردارها ایجاد کنیم:

کوتاه می کنیم:
بنابراین مختصات مربوطه متناسب هستند، بنابراین،

رابطه می تواند ایجاد شود و بالعکس، این یک گزینه معادل است:

برای خودآزمایی، می توان از این واقعیت استفاده کرد که بردارهای خطی به صورت خطی از طریق یکدیگر بیان می شوند. در این مورد برابری هایی وجود دارد . اعتبار آنها را می توان به راحتی از طریق عملیات ابتدایی با بردارها بررسی کرد:

ب) دو بردار مسطح اگر خطی نباشند (مستقل خطی) مبنایی را تشکیل می دهند. ما بردارها را برای همخطی بودن بررسی می کنیم . بیایید یک سیستم ایجاد کنیم:

از معادله اول نتیجه می شود که از معادله دوم نتیجه می شود که به این معنی است که سیستم ناسازگار است(بدون راه حل). بنابراین، مختصات متناظر بردارها متناسب نیستند.

نتیجه: بردارها به صورت خطی مستقل هستند و پایه را تشکیل می دهند.

نسخه ساده شده راه حل به این صورت است:

نسبت را از مختصات مربوطه بردارها بسازید :
از این رو، این بردارها به صورت خطی مستقل هستند و مبنایی را تشکیل می دهند.

معمولا بررسی کنندگان این گزینه را رد نمی کنند، اما در مواردی که برخی مختصات برابر با صفر هستند، مشکل ایجاد می شود. مثل این: . یا مثل این: . یا مثل این: . چگونه می توان از طریق نسبت در اینجا کار کرد؟ (واقعا نمی توان بر صفر تقسیم کرد). به همین دلیل است که من راه حل ساده شده را "foppish" نامیدم.

پاسخ:الف)، ب) شکل.

یک مثال خلاقانه کوچک برای یک راه حل مستقل:

مثال 2

در چه مقدار از بردارهای پارامتر خطی خواهد بود؟

در حل نمونه، پارامتر از طریق نسبت پیدا می شود.

یک روش جبری ظریف برای بررسی بردارها برای همخطی بودن وجود دارد. بیایید دانش خود را سیستماتیک کنیم و فقط آن را به عنوان نقطه پنجم اضافه کنیم:

برای دو بردار صفحه، عبارات زیر معادل هستند:

2) بردارها اساس را تشکیل می دهند.
3) بردارها خطی نیستند.

+ 5) تعیین کننده، متشکل از مختصات این بردارها، غیر صفر است.

به ترتیب، عبارات مقابل زیر معادل هستند:
1) بردارها به صورت خطی وابسته هستند.
2) بردارها مبنایی را تشکیل نمی دهند.
3) بردارها خطی هستند.
4) بردارها را می توان به صورت خطی از طریق یکدیگر بیان کرد.
+ 5) تعیین کننده متشکل از مختصات این بردارها برابر با صفر است..

من واقعاً، واقعاً امیدوارم که در حال حاضر همه اصطلاحات و عباراتی را که با آنها برخورد شده است، درک کرده باشید.

بیایید نگاهی دقیق تر به نکته جدید، پنجم بیندازیم: دو بردار صفحه خطی هستند اگر و فقط در صورتی که تعیین کننده متشکل از مختصات بردارهای داده شده برابر با صفر باشد.: برای استفاده از این ویژگی، البته باید بتوانید تعیین کننده ها را پیدا کنید.

تصمیم خواهیم گرفتمثال 1 به روش دوم:

الف) تعیین کننده را که از مختصات بردارها تشکیل شده است محاسبه کنید :
، بنابراین این بردارها خطی هستند.

ب) دو بردار مسطح اگر خطی نباشند (مستقل خطی) مبنایی را تشکیل می دهند. اجازه دهید دترمینان متشکل از مختصات بردارها را محاسبه کنیم :
، از این رو بردارها به صورت خطی مستقل هستند و یک پایه را تشکیل می دهند.

پاسخ:الف)، ب) شکل.

بسیار فشرده تر و زیباتر از راه حل با نسبت به نظر می رسد.

با کمک مواد در نظر گرفته شده، می توان نه تنها همخطی بردارها، بلکه موازی بودن قطعات، خطوط مستقیم را نیز اثبات کرد. چند مشکل با اشکال هندسی خاص را در نظر بگیرید.

مثال 3

رئوس یک چهارضلعی داده شده است. ثابت کنید که چهارضلعی متوازی الاضلاع است.

اثبات: نیازی به ایجاد نقشه در مسئله نیست، زیرا راه حل صرفاً تحلیلی خواهد بود. تعریف متوازی الاضلاع را به خاطر بسپار:
متوازی الاضلاع چهار ضلعی نامیده می شود که در آن اضلاع مقابل به صورت جفتی موازی هستند.

بنابراین لازم است ثابت شود:
1) توازی اضلاع مقابل و;
2) توازی اضلاع مقابل و .

ما ثابت می کنیم:

1) بردارها را بیابید:

2) بردارها را بیابید:

نتیجه همان بردار است ("طبق مدرسه" - بردارهای برابر). خطی بودن کاملاً واضح است، اما بهتر است با چیدمان درست تصمیم بگیرید. تعیین کننده را که از مختصات بردارها تشکیل شده است محاسبه کنید:
، بنابراین این بردارها خطی هستند و .

نتیجه: اضلاع مقابل یک چهار ضلعی به صورت جفتی موازی هستند، بنابراین طبق تعریف متوازی الاضلاع است. Q.E.D.

ارقام خوب و متفاوت تر:

مثال 4

رئوس یک چهارضلعی داده شده است. ثابت کنید که چهارضلعی ذوزنقه است.

برای فرمول دقیق تر اثبات، البته بهتر است که تعریف ذوزنقه را بدست آوریم، اما کافی است فقط به یاد بیاوریم که چگونه به نظر می رسد.

این یک وظیفه برای تصمیم گیری مستقل است. راه حل کامل در پایان درس.

و اکنون زمان آن است که به آرامی از هواپیما به فضا حرکت کنیم:

چگونه می توان همخطی بردارهای فضایی را تعیین کرد؟

قانون بسیار شبیه است. برای هم خطی بودن دو بردار فضایی، کافی و ضروری است که مختصات متناظر آنها متناسب با.

مثال 5

دریابید که آیا بردارهای فضایی زیر هم خط هستند:

آ) ؛
ب)
که در)

تصمیم:
الف) بررسی کنید که آیا ضریب تناسبی برای مختصات مربوط به بردارها وجود دارد:

سیستم هیچ راه حلی ندارد، به این معنی که بردارها خطی نیستند.

"ساده شده" با بررسی نسبت ساخته می شود. در این مورد:
- مختصات مربوطه متناسب نیستند، به این معنی که بردارها هم خط نیستند.

پاسخ:بردارها خطی نیستند.

ب-ج) اینها نکاتی برای تصمیم گیری مستقل هستند. از دو طریق آن را امتحان کنید.

روشی برای بررسی بردارهای فضایی برای همخطی بودن وجود دارد و از طریق یک تعیین کننده مرتبه سوم، این روش در مقاله پوشش داده شده است. حاصل ضرب بردارها.

همانند حالت صفحه، از ابزارهای در نظر گرفته شده می توان برای مطالعه موازی قطعات و خطوط فضایی استفاده کرد.

به بخش دوم خوش آمدید:

وابستگی خطی و استقلال بردارهای فضایی سه بعدی.
مبانی فضایی و سیستم مختصات وابسته

بسیاری از نظم هایی که در هواپیما در نظر گرفته ایم برای فضا نیز معتبر خواهد بود. من سعی کردم خلاصه نظریه را به حداقل برسانم، زیرا سهم شیر از اطلاعات قبلاً جویده شده است. با این وجود، توصیه می کنم که قسمت مقدماتی را با دقت مطالعه کنید، زیرا اصطلاحات و مفاهیم جدیدی ظاهر می شوند.

حال به جای صفحه میز کامپیوتر، فضای سه بعدی را بررسی می کنیم. ابتدا بیایید اساس آن را ایجاد کنیم. یک نفر اکنون در داخل خانه است، کسی در خارج از منزل است، اما در هر صورت، ما نمی توانیم از سه بعد: عرض، طول و ارتفاع دور شویم. بنابراین، سه بردار فضایی برای ساخت پایه مورد نیاز است. یک یا دو بردار کافی نیست، چهارمی اضافی است.

و دوباره روی انگشتان گرم می شویم. لطفا دست خود را بالا ببرید و در جهات مختلف باز کنید انگشت شست، اشاره و وسط. این ها بردار خواهند بود، در جهت های مختلف نگاه می کنند، طول های متفاوتی دارند و زوایای متفاوتی بین خود دارند. تبریک می گوییم، اساس فضای سه بعدی آماده است! به هر حال، لازم نیست این را به معلمان نشان دهید، مهم نیست که چگونه انگشتان خود را بچرخانید، اما نمی توانید از تعاریف دور شوید =)

در مرحله بعد یک سوال مهم می پرسیم آیا هر سه بردار اساس یک فضای سه بعدی را تشکیل می دهند؟? لطفا سه انگشت خود را محکم روی میز کامپیوتر فشار دهید. چی شد؟ سه بردار در یک صفحه قرار دارند، و به طور تقریبی، ما یکی از اندازه گیری ها - ارتفاع را از دست داده ایم. چنین بردارهایی هستند هم صفحهو کاملا بدیهی است که اساس فضای سه بعدی ایجاد نشده است.

لازم به ذکر است که بردارهای همسطح لزومی ندارد که در یک صفحه قرار بگیرند، آنها می توانند در صفحات موازی باشند (فقط این کار را با انگشتان خود انجام ندهید، فقط سالوادور دالی به این شکل خارج شد =)).

تعریف: بردارها نامیده می شوند هم صفحهاگر صفحه ای وجود داشته باشد که با آن موازی باشند. در اینجا منطقی است که اضافه کنیم که اگر چنین صفحه ای وجود نداشته باشد، بردارها همسطح نخواهند بود.

سه بردار همسطح همیشه به صورت خطی وابسته هستند، یعنی به صورت خطی از طریق یکدیگر بیان می شوند. برای سادگی، دوباره تصور کنید که آنها در یک صفحه قرار دارند. اولا، بردارها نه تنها همسطح هستند، بلکه می توانند هم خط باشند، سپس هر بردار را می توان از طریق هر بردار بیان کرد. در حالت دوم، اگر برای مثال، بردارها هم خط نباشند، بردار سوم از طریق آنها به روشی منحصر به فرد بیان می شود: (و چرا از مطالب بخش قبل به راحتی می توان حدس زد).

عکس آن نیز صادق است: سه بردار غیرهمسطح همیشه به صورت خطی مستقل هستند، یعنی به هیچ وجه از طریق یکدیگر بیان نمی شوند. و بدیهی است که تنها چنین بردارهایی می توانند اساس یک فضای سه بعدی را تشکیل دهند.

تعریف: اساس فضای سه بعدیسه گانه از بردارهای مستقل خطی (غیر همسطح) نامیده می شود، به ترتیب خاصی گرفته شده است، در حالی که هر بردار از فضا تنها راهدر مبنای داده شده گسترش می یابد، جایی که مختصات بردار در مبنای داده شده است

به عنوان یادآوری، همچنین می توانید بگویید که یک بردار به صورت نمایش داده می شود ترکیب خطیبردارهای پایه

مفهوم یک سیستم مختصات دقیقاً به همان شکلی که برای حالت صفحه معرفی شده است، یک نقطه و هر سه بردار مستقل خطی کافی است:

اصل و نسب، و غیر همسطحبردارها به ترتیب خاصی گرفته شده است، تنظیم سیستم مختصات افین فضای سه بعدی :

البته، شبکه مختصات "مورب" و ناخوشایند است، اما، با این وجود، سیستم مختصات ساخته شده به ما اجازه می دهد تا قطعامختصات هر بردار و مختصات هر نقطه در فضا را تعیین کنید. مشابه هواپیما، در سیستم مختصات افین فضا، برخی از فرمول هایی که قبلا ذکر کردم کار نمی کنند.

همانطور که همه می توانند حدس بزنند، آشناترین و راحت ترین مورد خاص یک سیستم مختصات افین است سیستم مختصات فضایی مستطیلی:

نقطه ای در فضا نامیده می شود اصل و نسب، و متعارفمجموعه پایه سیستم مختصات دکارتی فضا . عکس آشنا:

قبل از انجام کارهای عملی، دوباره اطلاعات را سیستماتیک می کنیم:

برای سه بردار فضایی، عبارات زیر معادل هستند:
1) بردارها به صورت خطی مستقل هستند.
2) بردارها اساس را تشکیل می دهند.
3) بردارها همسطح نیستند.
4) بردارها را نمی توان به صورت خطی از طریق یکدیگر بیان کرد.
5) تعیین کننده، متشکل از مختصات این بردارها، با صفر متفاوت است.

به نظر من اظهارات مخالف قابل درک است.

وابستگی خطی / استقلال بردارهای فضا به طور سنتی با استفاده از تعیین کننده بررسی می شود (مورد 5). کارهای عملی باقیمانده ماهیت جبری مشخصی خواهند داشت. وقت آن است که چوب هندسی را به میخ آویزان کنید و چوب بیسبال جبر خطی را به کار بگیرید:

سه بردار فضاییهمسطح هستند اگر و فقط در صورتی که تعیین کننده متشکل از مختصات بردارهای داده شده برابر با صفر باشد: .

توجه شما را به یک نکته ظریف فنی کوچک جلب می کنم: مختصات بردارها را می توان نه تنها در ستون ها، بلکه در ردیف ها نیز نوشت (مقدار تعیین کننده از این تغییر نمی کند - ویژگی های تعیین کننده ها را ببینید). اما در ستون ها بسیار بهتر است، زیرا برای حل برخی از مشکلات عملی مفیدتر است.

برای آن دسته از خوانندگانی که روش‌های محاسبه تعیین‌کننده‌ها را کمی فراموش کرده‌اند، یا شاید اصلاً جهت‌گیری ضعیفی دارند، یکی از قدیمی‌ترین درس‌های خود را توصیه می‌کنم: چگونه تعیین کننده را محاسبه کنیم؟

مثال 6

بررسی کنید که آیا بردارهای زیر اساس یک فضای سه بعدی را تشکیل می دهند:

تصمیم گیری: در واقع کل راه حل به محاسبه دترمینان می رسد.

الف) تعیین کننده را که از مختصات بردارها تشکیل شده است محاسبه کنید (تعیین کننده در خط اول بسط می یابد):

، به این معنی که بردارها مستقل خطی هستند (همسطح نیستند) و اساس یک فضای سه بعدی را تشکیل می دهند.

پاسخ: این بردارها اساس را تشکیل می دهند

ب) این نقطه ای برای تصمیم گیری مستقل است. حل کامل و پاسخ در پایان درس.

همچنین وظایف خلاقانه وجود دارد:

مثال 7

در چه مقدار از پارامتر بردارها همسطح خواهند بود؟

تصمیم گیری: بردارها همسطح هستند اگر و فقط در صورتی که تعیین کننده متشکل از مختصات بردارهای داده شده برابر با صفر باشد:

در اصل، حل یک معادله با یک دترمینال مورد نیاز است. ما مانند بادبادک ها به سمت صفرها در جربوآها پرواز می کنیم - سودآورتر است که تعیین کننده را در خط دوم باز کنیم و فوراً از شر معایب خلاص شویم:

ما ساده سازی های بیشتری انجام می دهیم و ماده را به ساده ترین معادله خطی کاهش می دهیم:

پاسخ: در

بررسی اینجا آسان است، برای این کار باید مقدار حاصل را با تعیین کننده اصلی جایگزین کنید و مطمئن شوید که با بازگشایی آن

در خاتمه، بیایید یک مسئله معمولی دیگر را در نظر بگیریم که بیشتر ماهیت جبری دارد و به طور سنتی در درس جبر خطی گنجانده شده است. آنقدر رایج است که سزاوار یک موضوع جداگانه است:

ثابت کنید که 3 بردار اساس یک فضای سه بعدی را تشکیل می دهند
و مختصات بردار 4 را در مبنای داده شده بیابید

مثال 8

بردارها داده شده است. نشان دهید که بردارها اساس فضای سه بعدی را تشکیل می دهند و مختصات بردار را در این مبنا پیدا کنید.

تصمیم گیری: اول به شرط بپردازیم. بر اساس شرط، چهار بردار داده می شود، و همانطور که می بینید، آنها قبلاً مختصاتی دارند. اساس چیست - ما علاقه ای نداریم. و نکته زیر جالب است: سه بردار ممکن است پایه جدیدی را تشکیل دهند. و مرحله اول کاملاً مشابه جواب مثال 6 است، باید بررسی شود که آیا بردارها واقعاً مستقل خطی هستند یا خیر:

تعیین کننده را که از مختصات بردارها تشکیل شده است محاسبه کنید:

، از این رو بردارها به صورت خطی مستقل هستند و اساس یک فضای سه بعدی را تشکیل می دهند.

! مهم : مختصات برداری لزومابنویس به ستون هاتعیین کننده، نه رشته ها. در غیر این صورت، در الگوریتم حل بعدی سردرگمی وجود خواهد داشت.

در هندسه، یک بردار به عنوان یک قطعه جهت دار درک می شود و بردارهایی که با ترجمه موازی از یکدیگر به دست می آیند برابر در نظر گرفته می شوند. همه بردارهای مساوی به عنوان بردار یکسان در نظر گرفته می شوند. ابتدای بردار را می توان در هر نقطه ای از فضا یا صفحه قرار داد.

اگر مختصات انتهای بردار در فضا داده شود: آ(ایکس 1 , y 1 , z 1), ب(ایکس 2 , y 2 , z 2) سپس

= (ایکس 2 – ایکس 1 , y 2 – y 1 , z 2 – z 1). (1)

فرمول مشابهی در هواپیما وجود دارد. این بدان معنی است که یک بردار را می توان به عنوان یک رشته مختصات نوشت. عملیات بردارها، - جمع و ضرب در یک عدد، روی رشته ها جزء به جزء انجام می شود. این امکان بسط مفهوم بردار را فراهم می کند و یک بردار را به عنوان هر رشته ای از اعداد درک می کند. به عنوان مثال، حل یک سیستم معادلات خطی و همچنین هر مجموعه ای از مقادیر متغیرهای سیستم را می توان به عنوان یک بردار در نظر گرفت.

در رشته هایی با طول یکسان، عملیات جمع بر اساس قانون انجام می شود

(a 1 , a 2 , … , a n) + (b 1 , b 2 , … , b n) = (a 1 + b 1 , a 2 + b 2 , … , a n+b n). (2)

ضرب یک رشته در یک عدد طبق قانون انجام می شود

l(a 1 , a 2 , … , a n) = (la 1 , la 2 , … , la n). (3)

مجموعه ای از بردارهای ردیف با طول معین nبا اعمال نشان داده شده جمع بردار و ضرب در یک عدد، ساختار جبری به نام فضای خطی n بعدی.

ترکیب خطی از بردارها یک بردار است ، جایی که λ 1 , ... , λ مترضرایب دلخواه هستند.

سیستمی از بردارها را در صورتی وابسته خطی می نامند که ترکیب خطی آن برابر با 1 وجود داشته باشد که حداقل یک ضریب غیر صفر داشته باشد.

سیستمی از بردارها به صورت مستقل خطی نامیده می‌شود که در هر یک از ترکیب‌های خطی آن برابر با، همه ضرایب صفر باشند.

بنابراین، حل مسئله وابستگی خطی سیستم بردارها به حل معادله کاهش می یابد.

ایکس 1 + ایکس 2 + … + x m = . (4)

اگر این معادله دارای راه حل های غیر صفر باشد، سیستم بردارها به صورت خطی وابسته است. اگر جواب صفر منحصر به فرد باشد، سیستم بردارها مستقل خطی است.

برای حل سیستم (4)، برای وضوح، بردارها را می توان نه به صورت ردیف، بلکه به صورت ستون نوشت.

سپس پس از انجام تبدیلات در سمت چپ به سیستم معادلات خطی معادل معادله (4) می رسیم. ماتریس اصلی این سیستم از مختصات بردارهای اصلی که در ستون ها چیده شده اند تشکیل می شود. ستون اعضای آزاد در اینجا مورد نیاز نیست، زیرا سیستم همگن است.

اساسسیستم بردارها (متناهی یا نامتناهی، به ویژه، کل فضای خطی) زیرسیستم مستقل خطی غیر خالی آن است که از طریق آن می توان هر بردار سیستم را بیان کرد.

مثال 1.5.2.اساس سیستم بردارها را بیابید = (1، 2، 2، 4)، = (2، 3، 5، 1)، = (3، 4، 8، -2)، = (2، 5، 0، 3) و سایر بردارها را از طریق پایه بیان کنید.

تصمیم گیری. ماتریسی می سازیم که در آن مختصات این بردارها به صورت ستونی چیده شده اند. این ماتریس سیستم است ایکس 1 + ایکس 2 + ایکس 3 + ایکس 4 = . ماتریس را به شکل پلکانی می آوریم:

~ ~ ~

اساس این سیستم از بردارها توسط بردارهای , , , که مربوط به عناصر اصلی ردیف هایی است که با دایره مشخص شده اند تشکیل می شود. برای بیان بردار، معادله را حل می کنیم ایکس 1 + ایکس 2 + ایکس 4 = . به سیستمی از معادلات خطی تقلیل می‌یابد که ماتریس آن از اصل با مرتب کردن مجدد ستون مربوط به، به محل ستون عبارت‌های آزاد به دست می‌آید. بنابراین، هنگام کاهش به یک فرم پله‌ای، همان تبدیل‌های فوق روی ماتریس انجام می‌شود. این بدان معنی است که ما می توانیم با ایجاد جایگشت های لازم برای ستون های موجود در آن، ماتریس حاصل را به صورت پلکانی استفاده کنیم: ستون های دارای دایره در سمت چپ نوار عمودی قرار می گیرند و ستون مربوط به بردار در سمت راست قرار می گیرد. از نوار

ما متوالی پیدا می کنیم:

ایکس 4 = 0;

ایکس 2 = 2;

ایکس 1 + 4 = 3, ایکس 1 = –1;

اظهار نظر. اگر لازم باشد چندین بردار از طریق پایه بیان شود، برای هر یک از آنها سیستم معادلات خطی مربوطه ساخته می شود. این سیستم ها فقط در ستون های اعضای آزاد متفاوت خواهند بود. در این حالت هر سیستمی مستقل از سایرین حل می شود.

تمرین 1.4.اساس سیستم بردارها را بیابید و بقیه بردارها را بر اساس مبنا بیان کنید:

a) = (1، 3، 2، 0)، = (3، 4، 2، 1)، = (1، –2، –2، 1)، = (3، 5، 1، 2);

ب) = (2، 1، 2، 3)، = (1، 2، 2، 3)، = (3، -1، 2، 2)، = (4، -2، 2، 2)؛

ج) = (1، 2، 3)، = (2، 4، 3)، = (3، 6، 6)، = (4، -2، 1); = (2، -6، -2).

در یک سیستم معین از بردارها، یک پایه معمولاً می تواند به روش های مختلف متمایز شود، اما همه پایه ها دارای تعداد یکسانی بردار خواهند بود. به تعداد بردارها در پایه یک فضای خطی، بعد فضا می گویند. برای nفضای خطی بعدی nبعد فضا است، زیرا این فضا دارای مبنای استاندارد = (1، 0، …، 0)، = (0، 1، …، 0)، …، = (0، 0، …، 1) است. از این طریق، هر بردار = (a 1 , a 2 , … , a n) به صورت زیر بیان می شود:

= (a 1 , 0 , … , 0) + (0, a 2 , … , 0) + … + (0, 0, … , a n) =

A 1 (1، 0، …، 0) + a 2 (0، 1، …، 0) + … + a n(0, 0, ... ,1) = a 1 + a 2 + ... + a n .

بنابراین، اجزای ردیف بردار = (a 1 , a 2 , … , a n) ضرایب آن در بسط بر حسب مبنای استاندارد می باشد.

خطوط مستقیم در هواپیما

مسئله هندسه تحلیلی استفاده از روش مختصات در مسائل هندسی است. بنابراین، مسئله به شکل جبری ترجمه شده و با استفاده از جبر حل می شود.

اساس سیستم بردارها و بردارهایی که در مبنا گنجانده نشده اند را بیابید، بر اساس آن بسط دهید:

آ 1 = {5, 2, -3, 1}, آ 2 = {4, 1, -2, 3}, آ 3 = {1, 1, -1, -2}, آ 4 = {3, 4, -1, 2}, آ 5 = {13, 8, -7, 4}.

تصمیم گیری. یک سیستم همگن از معادلات خطی را در نظر بگیرید

آ 1 ایکس 1 + آ 2 ایکس 2 + آ 3 ایکس 3 + آ 4 ایکس 4 + آ 5 ایکس 5 = 0

یا گسترش یافته است.

ما این سیستم را با استفاده از روش گاوسی، بدون جابجایی سطرها و ستون ها، و علاوه بر این، انتخاب عنصر اصلی نه در گوشه بالا سمت چپ، بلکه در سراسر ردیف حل خواهیم کرد. وظیفه این است که قسمت مورب سیستم تبدیل شده بردارها را انتخاب کنید.

~ ~

~ ~ ~ .

سیستم مجاز از بردارها که معادل بردار اصلی است دارای فرم است

آ 1 1 ایکس 1 + آ 2 1 ایکس 2 + آ 3 1 ایکس 3 + آ 4 1 ایکس 4 + آ 5 1 ایکس 5 = 0 ,

جایی که آ 1 1 = , آ 2 1 = , آ 3 1 = , آ 4 1 = , آ 5 1 = . (1)

بردارها آ 1 1 , آ 3 1 , آ 4 1 یک سیستم مورب را تشکیل می دهند. از این رو بردارها آ 1 , آ 3 , آ 4 اساس سیستم بردارها را تشکیل می دهند آ 1 , آ 2 , آ 3 , آ 4 , آ 5 .

اکنون بردارها را گسترش می دهیم آ 2 و آ 5 بر اساس آ 1 , آ 3 , آ 4 . برای این کار ابتدا بردارهای مربوطه را گسترش می دهیم آ 2 1 و آ 5 1 سیستم مورب آ 1 1 , آ 3 1 , آ 4 1، با توجه به اینکه ضرایب انبساط برداری در سیستم مورب مختصات آن است. x i.

از (1) داریم:

آ 2 1 = آ 3 1 (-1) + آ 4 1 0 + آ 1 1 1 آ 2 1 = آ 1 1 – آ 3 1 .

آ 5 1 = آ 3 1 0 + آ 4 1 1 + آ 1 1 2 آ 5 1 = 2آ 1 1 + آ 4 1 .

بردارها آ 2 و آ 5 گسترش در اساس آ 1 , آ 3 , آ 4 با ضرایبی مشابه بردارها آ 2 1 و آ 5 1 سیستم مورب آ 1 1 , آ 3 1 , آ 4 1 (آن ضرایب x i). از این رو،

آ 2 = آ 1 – آ 3 , آ 5 = 2آ 1 + آ 4 .

وظایف یکیاساس سیستم بردارها را بیابید و بردارهایی که در مبنا قرار نمی گیرند، بر اساس مبنا بسط دهید:

1. آ 1 = { 1, 2, 1 }, آ 2 = { 2, 1, 3 }, آ 3 = { 1, 5, 0 }, آ 4 = { 2, -2, 4 }.

2. آ 1 = { 1, 1, 2 }, آ 2 = { 0, 1, 2 }, آ 3 = { 2, 1, -4 }, آ 4 = { 1, 1, 0 }.

3. آ 1 = { 1, -2, 3 }, آ 2 = { 0, 1, -1 }, آ 3 = { 1, 3, 0 }, آ 4 = { 0, -7, 3 }, آ 5 = { 1, 1, 1 }.

4. آ 1 = { 1, 2, -2 }, آ 2 = { 0, -1, 4 }, آ 3 = { 2, -3, 3 }.

2. تمام پایه های یک سیستم بردار را بیابید:

1. آ 1 = { 1, 1, 2 }, آ 2 = { 3, 1, 2 }, آ 3 = { 1, 2, 1 }, آ 4 = { 2, 1, 2 }.

2. آ 1 = { 1, 1, 1 }, آ 2 = { -3, -5, 5 }, آ 3 = { 3, 4, -1 }, آ 4 = { 1, -1, 4 }.