Piramidin yan yüzlerinin eğim açıları. Piramit. Kesik piramit. Düzenli bir kesik piramit için formül doğrudur

Yan yüzlerin tabana dik olduğu piramitlerin özelliklerini düşünün.

Eğer bir bir piramidin iki bitişik yan yüzü tabana diktir, o zamanlar bu yüzlerin ortak yan kenarı piramidin yüksekliğidir.. Görev bunu söylüyorsa piramidin kenarı yüksekliğidir, o zaman bu tür piramitlerden bahsediyoruz.

Piramidin tabana dik olan yüzleri dik açılı üçgenlerdir.

Piramidin tabanı üçgen ise

Böyle bir piramidin yan yüzeyi genellikle tüm yan yüzlerin alanlarının toplamı olarak aranır.

Piramidin tabanı, tabana dik olmayan bir yüzün ortogonal izdüşümüdür (bu durumda, SBC). Dolayısıyla, ortogonal izdüşüm alanı teoremine göre, taban alanı, bu yüzün alanının çarpımı ile taban düzlemi arasındaki açının kosinüsüne eşittir.

Piramidin tabanı bir dik üçgen ise

Bu durumda piramidin tüm yüzleri dik üçgendir.

SA piramidin yüksekliği olduğu için SAB ve SAC üçgenleri dik açılıdır. ABC üçgeni bir dik üçgendir.

SBC üçgeninin dik açılı olduğu gerçeği, üç dik üzerindeki teoremden kaynaklanmaktadır (AB, eğik SB'nin taban düzlemi üzerindeki izdüşümüdür. AB, BC'ye koşula göre dik olduğundan, SB de BC'ye diktir. ).

Bu durumda SBC yan yüzü ile taban arasındaki açı ABS açısıdır.

Yan yüzey alanı, dik üçgenlerin alanlarının toplamına eşittir:

Bu durumda beri

Piramidin tabanı ikizkenar üçgen ise

Bu durumda, BCS yan yüzünün düzlemi ile taban düzlemi arasındaki açı, AFS açısıdır; burada AF, ABC ikizkenar üçgeninin yüksekliği, medyanı ve açıortayıdır.

Benzer şekilde - piramidin tabanında eşkenar bir ABC üçgeni varsa.

Piramidin tabanı paralelkenar ise

Bu durumda, piramidin tabanı, tabana dik olmayan yan yüzlerin dik bir izdüşümüdür.

Tabanı iki üçgene bölersek,

burada α ve β sırasıyla ADS ve CDS düzlemleri ile taban düzlemi arasındaki açılardır.

BF ve BK paralelkenarın yükseklikleri ise, BFS açısı CDS yan yüzünün taban düzlemine eğim açısıdır ve BKS açısı ADS yüzünün eğim açısıdır.

(çizim B'nin geniş açı olduğu durum için yapılmıştır).

Piramidin tabanı eşkenar dörtgen ABCD ise, BFS ve BKS açıları eşittir. Bu durumda ABS ve CBS ile ADS ve CDS üçgenleri de eşittir.

Piramidin tabanı dikdörtgen ise

Bu durumda, yan yüz SAD düzlemi ile taban düzlemi arasındaki açı SAB açısıdır,

ve SCD yan yüzünün düzlemi ile taban düzlemi arasındaki açı, SCB açısıdır.

(üç dik teoremi ile).

Hatırlayın: özlü söz, piramidin tepesinden tabanın kenarına çizilen yan yüzünün yüksekliğidir.
teorem 5 . Piramidin tüm yan yüzleri taban düzlemine aynı açıda eğimliyse, böyle bir piramidin tabanına bir daire çizilebilir ve tepeden tabana indirilen yükseklik, piramidin merkezine düşer. tabanda yazılı daire.
Bu teorem şu şekilde de formüle edilebilir:
Teorem 5.1 . Bir piramidin tüm özlü sözleri eşitse, böyle bir piramidin tabanına bir daire yazılabilir ve tepeden tabana indirilen yükseklik, tabanda yazılı dairenin merkezine düşer.
Dörtgen bir piramit örneği kullanarak teoremi kanıtlayalım. KABCD piramidi verilsin, K üst, ABCD taban olsun. Piramidin KO'sunun yüksekliğini çizin. Her bir yan yüzde, piramidin tepesinden tabanın yanına bir yükseklik çiziyoruz. Taban düzleminde, O noktasını (yüksekliğin tabanı) bu yüksekliklerin tabanlarının noktası - apothem ile birleştiririz. OP, OT, OM ve OE sırasıyla AB, BC, CD ve AD'ye diktir (üç dik teoremi). Tanım olarak, KRO, KTO, KMO, KEO açıları, karşılık gelen yan yüzler ile ABCD tabanı arasındaki dihedral açıların lineer açılarıdır. KO'nun yüksekliği tabana diktir, bu nedenle bu düzlemdeki herhangi bir düz çizgiye diktir, yani. OR, OT, OM ve OE düz çizgilerine dik. Bu, KRO, KTO, KMO, KEO üçgenlerinin dikdörtgen olduğunu söylüyor.
Duruma göre (Teorem 5), KRO, KTO, KMO, KEO açıları eşittir. KRO, KTO, KMO, KEO üçgenlerini düşünün, bunlar dikdörtgen ve eşittir (bacak ve dar açı boyunca, KO - ortak ve KRO, KTO, KMO, KEO açıları koşula göre eşittir).
Duruma göre (teorem 5.1) KR, KT, KM ve KE eşittir, bu nedenle KRO, KTO, KMO, KEO üçgenleri dikdörtgendir ve bacak ve hipotenüs bakımından eşittir.
Bu üçgenlerin eşitliğinden, ilgili kenarlarının VEYA, OT, OM ve OE eşit olduğu sonucu çıkar, bu, ABCD dörtgeninde kenarlarından eşit uzaklıkta bir nokta olduğu anlamına gelir, yani içine bir daire yazılabilir. .

Teorem 6 . Piramidin tüm yan kenarları taban düzlemine aynı açıda eğimliyse, o zaman böyle bir piramidin tabanına yakın bir daire tanımlanabilir ve tepeden tabana indirilen yükseklik merkeze düşer. tabanın yakınında açıklanan daire.
Bu teorem şu şekilde de formüle edilebilir:
Teorem 6.1 . Piramidin tüm yan kenarları eşitse, böyle bir piramidin tabanına yakın bir daire çizilebilir ve tepeden tabana indirilen yükseklik, çevrelenmiş dairenin tabanına yakın olan merkezine düşer.
Dörtgen bir piramit örneği kullanarak teoremi kanıtlayalım. KABCD piramidi verilsin, K üst, ABCD taban olsun. Piramidin KO'sunun yüksekliğini çizin. Taban düzleminde, O noktasını (yüksekliğin tabanı) A, B, C ve D tabanının tüm köşeleriyle birleştirin. Açı KBO, KB kenarı ile taban düzlemi (yükseklik tabanı) arasındaki açıdır. çizgi ile düzlem arasındaki açı, bu çizgi ile bu düzleme izdüşümü arasındaki açıdır). Aynı şekilde, KSO, KAO ve KDO açılarının, karşılık gelen KS, KA ve KD kenarlarının taban düzlemiyle oluşturduğu açılar olduğunu kanıtlıyoruz. KO'nun yüksekliği tabana diktir, bu nedenle bu düzlemdeki herhangi bir düz çizgiye diktir, yani. OA, OB, OC ve OD çizgilerine dik. Bu, KAO, KBO, KCO, KDO üçgenlerinin dikdörtgen olduğunu söylüyor.
KVO, KSO, KAO ve KDO açıları eşittir (Teorem 6'nın koşullarına göre). KAO, KBO, KCO, KDO üçgenlerini düşünün, bunlar dikdörtgen ve eşittir (bacak ve dar açı boyunca, KO ortaktır ve KAO, KVO, KSO, KDO açıları koşula göre eşittir).
Teorem 6.1'i kanıtlayarak, KAO, KBO, KCO, KDO üçgenlerini de göz önünde bulunduruyoruz, bunlar dikdörtgen ve bacak ve hipotenüste eşittir (KO - genel, KA=KV=KS=KD teoremin hipotezine göre).
Bu üçgenlerin eşitliğinden, ilgili kenarlarının OA, OB, OS ve OD eşit olduğu sonucu çıkar, bu, tabanda ABCD dörtgeninin köşelerinden eşit uzaklıkta bir nokta olduğu anlamına gelir, yani bir daire çizilebilir. etrafında.

Piramit yüzlerinden biri çokgen olan çokyüzlü olarak adlandırılır ( temel ) ve diğer tüm yüzler ortak bir tepe noktasına sahip üçgenlerdir ( yan yüzler ) (Şek. 15). piramit denir doğru , tabanı düzenli bir çokgen ise ve piramidin tepesi tabanın merkezine yansıtılırsa (Şek. 16). Tüm kenarları eşit olan üçgen piramit denir tetrahedron .

yan kaburga piramit, yan yüzün tabana ait olmayan tarafına denir. Yükseklik piramit, tepesinden taban düzlemine olan mesafedir. Düzgün bir piramidin tüm yan kenarları birbirine eşittir, tüm yan yüzler eşit ikizkenar üçgenlerdir. Köşeden çizilen düzgün bir piramidin yan yüzünün yüksekliğine denir. özlü söz . diyagonal bölüm Piramidin bir bölümüne, aynı yüze ait olmayan iki yan kenardan geçen düzlem denir.

yan yüzey alanı Piramit, tüm yan yüzlerin alanlarının toplamı olarak adlandırılır. Tam yüzey alanı tüm yan yüzlerin ve tabanın alanlarının toplamıdır.

teoremler

1. Bir piramitte tüm yan kenarlar taban düzlemine eşit derecede eğimliyse, piramidin tepesi, tabanın yakınındaki çevrelenmiş dairenin merkezine yansıtılır.

2. Bir piramitte tüm yan kenarların uzunlukları eşitse, piramidin tepesi, tabanın yakınında çevrelenmiş dairenin merkezine yansıtılır.

3. Piramitte tüm yüzler taban düzlemine eşit eğimliyse, piramidin tepesi tabanda yazılı dairenin merkezine yansıtılır.

Rastgele bir piramidin hacmini hesaplamak için formül doğrudur:

nerede V- Ses;

ana- taban alanı;

H piramidin yüksekliğidir.

Düzenli bir piramit için aşağıdaki formüller doğrudur:

nerede p- tabanın çevresi;

bir- özlü söz;

H- yükseklik;

S dolu

S tarafı

ana- taban alanı;

V düzgün bir piramidin hacmidir.

kesik piramit taban ile piramidin tabanına paralel olan kesme düzlemi arasında kalan piramidin parçası olarak adlandırılır (Şekil 17). Doğru kesik piramit düzgün bir piramidin, tabanı ile tabanına paralel bir kesme düzlemi arasında kalan parçası olarak adlandırılır.

Vakıflar kesik piramit - benzer çokgenler. yan yüzler - yamuk. Yükseklik kesik piramit, tabanları arasındaki mesafe olarak adlandırılır. Diyagonal Kesik bir piramit, aynı yüzde yer almayan köşelerini birleştiren bir segmenttir. diyagonal bölüm Kesik bir piramidin bir bölümüne, aynı yüze ait olmayan iki yan kenardan geçen bir düzlem denir.

Kesik bir piramit için formüller geçerlidir:

(4)

nerede S 1 , S 2 - üst ve alt tabanların alanları;

S dolu toplam yüzey alanıdır;

S tarafı yan yüzey alanıdır;

H- yükseklik;

V kesik piramidin hacmidir.

Düzenli bir kesik piramit için aşağıdaki formül doğrudur:

nerede p 1 , p 2 - taban çevreleri;

bir- düzenli bir kesik piramidin özü.

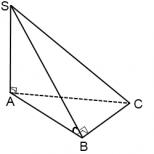
örnek 1 Düzgün üçgen piramitlerde tabandaki dihedral açı 60º'dir. Yan kenarın taban düzlemine eğim açısının tanjantını bulun.

Karar. Bir çizim yapalım (Şek. 18).

Piramit düzenlidir, bu, tabanın bir eşkenar üçgen olduğu ve tüm yan yüzlerin eşit ikizkenar üçgenler olduğu anlamına gelir. Tabandaki dihedral açı, piramidin yan yüzünün taban düzlemine olan eğim açısıdır. Doğrusal açı açı olacaktır a iki dikme arasında: yani. Piramidin tepesi üçgenin merkezine yansıtılır (sınırlandırılmış dairenin merkezi ve üçgendeki yazılı daire ABC). Yan nervürün eğim açısı (örneğin SB) kenarın kendisi ile taban düzlemine izdüşümü arasındaki açıdır. kaburga için SB bu açı açı olacak SBD. Teğeti bulmak için bacakları bilmeniz gerekir. BÖYLE ve OB. Segmentin uzunluğu olsun BD 3 a. nokta Öçizgi segmenti BD parçalara ayrılır: ve BÖYLE: Bulduğumuz:

Cevap:

Örnek 2 Tabanlarının köşegenleri cm ve cm ve yüksekliği 4 cm ise düzgün bir kesik dörtgen piramidin hacmini bulun.

Karar. Kesik bir piramidin hacmini bulmak için formül (4)'ü kullanırız. Tabanların alanlarını bulmak için köşegenlerini bilerek taban karelerinin kenarlarını bulmanız gerekir. Tabanların kenarları sırasıyla 2 cm ve 8 cm'dir Bu, tabanların alanları anlamına gelir ve Tüm verileri formüle koyarak, kesilmiş piramidin hacmini hesaplarız:

Cevap: 112 cm3.

Örnek 3 Tabanlarının kenarları 10 cm ve 4 cm olan ve piramidin yüksekliği 2 cm olan düzgün bir üçgen kesik piramidin yan yüzünün alanını bulun.

Karar. Bir çizim yapalım (Şekil 19).

Bu piramidin yan yüzü bir ikizkenar yamuktur. Bir yamuğun alanını hesaplamak için tabanları ve yüksekliği bilmeniz gerekir. Bazlar duruma göre verilmiştir, sadece yükseklik bilinmemektedir. Nereden bul ANCAK 1 E bir noktadan dik ANCAK 1 alt tabanın düzleminde, A 1 D- dik ANCAK 1 AC. ANCAK 1 E\u003d 2 cm, çünkü bu piramidin yüksekliğidir. Bulmak için DEüstten görünümü tasvir edeceğimiz ek bir çizim yapacağız (Şek. 20). Nokta Ö- üst ve alt tabanların merkezlerinin izdüşümü. beri (bkz. Şekil 20) ve Öte yandan TAMAM yazılı dairenin yarıçapı ve OM yazılı dairenin yarıçapı:

MK=DE.

Pisagor teoremine göre

Yan yüz alanı:

Cevap:

Örnek 4 Piramidin tabanında, tabanları olan bir ikizkenar yamuk bulunur. a ve b (a> b). Her bir yan yüz, piramidin tabanının düzlemine eşit bir açı oluşturur. j. Piramidin toplam yüzey alanını bulun.

Karar. Bir çizim yapalım (Şek. 21). Piramidin toplam yüzey alanı SABCD alanların toplamına ve yamuğun alanına eşittir ABCD.

Piramidin tüm yüzleri taban düzlemine eşit derecede eğimliyse, tepe noktası tabanda yazılı dairenin merkezine yansıtılır ifadesini kullanırız. Nokta Ö- köşe projeksiyonu S piramidin tabanında. Üçgen SODüçgenin ortogonal izdüşümüdür CSD temel düzleme. Düz bir figürün ortogonal izdüşümü alanındaki teoreme göre şunları elde ederiz:

Benzer şekilde, şu anlama gelir Böylece sorun yamuğun alanını bulmaya indirgendi. ABCD. Bir yamuk çiz ABCD ayrı olarak (Şek. 22). Nokta Ö yamukta yazılı bir dairenin merkezidir.

Bir daire yamukta yazılabileceğinden, o zaman veya Pisagor teoremine göre