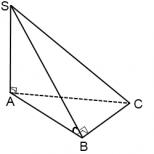
Uhly sklonu bočných plôch pyramídy. Pyramída. Zrezaná pyramída. Pre pravidelnú skrátenú pyramídu platí vzorec

Zvážte vlastnosti pyramíd, v ktorých sú bočné steny kolmé na základňu.

Ak dve susedné bočné strany pyramídy sú kolmé na základňu, potom spoločná bočná hrana týchto plôch je výška pyramídy. Ak to hovorí úloha okraj pyramídy je jej výška, potom hovoríme o tomto type pyramíd.

Plochy pyramídy kolmé na základňu sú pravouhlé trojuholníky.

Ak je základňou pyramídy trojuholník

Bočný povrch takejto pyramídy sa všeobecne hľadá ako súčet plôch všetkých bočných stien.

Základňa pyramídy je ortogonálna projekcia tváre, ktorá nie je kolmá na základňu (v tomto prípade SBC). Takže podľa vety o ortogonálnej projekčnej ploche sa základná plocha rovná súčinu plochy tejto plochy kosínusom uhla medzi ňou a základnou rovinou.

Ak je základňou pyramídy pravouhlý trojuholník

V tomto prípade všetky strany pyramídy sú pravouhlé trojuholníky.

Trojuholníky SAB a SAC sú pravouhlé, pretože SA je výška pyramídy. Trojuholník ABC je pravouhlý trojuholník.

To, že trojuholník SBC je pravouhlý vyplýva z vety o troch odvesniciach (AB je priemet šikmej SB do roviny podstavy. Keďže AB je podľa podmienky kolmá na BC, tak aj SB je kolmá na BC. ).

Uhol medzi bočnou stranou SBC a základňou je v tomto prípade uhol ABS.

Bočný povrch sa rovná súčtu plôch pravouhlých trojuholníkov:

Keďže v tomto prípade

Ak je základňou pyramídy rovnoramenný trojuholník

V tomto prípade je uhol medzi rovinou bočnej plochy BCS a rovinou základne uhol AFS, kde AF je nadmorská výška, medián a stred rovnoramenného trojuholníka ABC.

Podobne - ak na základni pyramídy leží rovnostranný trojuholník ABC.

Ak je základňou pyramídy rovnobežník

V tomto prípade je základňa pyramídy ortogonálnym priemetom bočných plôch, ktoré nie sú kolmé na základňu.

Ak rozdelíme základňu na dva trojuholníky, tak

kde α a β sú v tomto poradí uhly medzi rovinami ADS a CDS a základnou rovinou.

Ak BF a BK sú výšky rovnobežníka, potom uhol BFS je uhol sklonu bočnej plochy CDS k základnej rovine a uhol BKS je uhol sklonu plochy ADS.

(výkres je urobený pre prípad, keď B je tupý uhol).

Ak je základňou pyramídy kosoštvorec ABCD, potom sú uhly BFS a BKS rovnaké. Trojuholníky ABS a CBS, ako aj ADS a CDS sú v tomto prípade rovnaké.

Ak je základňou pyramídy obdĺžnik

V tomto prípade je uhol medzi rovinou bočnej plochy SAD a rovinou základne uhol SAB,

a uhol medzi rovinou bočnej plochy SCD a rovinou základne je uhol SCB

(podľa vety o troch kolmých).

Pripomeňme si: apotém je výška bočnej steny pyramídy, nakreslená zhora po okraj základne.
Veta 5 . Ak sú všetky bočné strany pyramídy naklonené k rovine základne pod rovnakým uhlom, potom môže byť do základne takejto pyramídy vpísaný kruh a výška znížená zhora na základňu spadá do stredu kruh vpísaný do základne.
Túto vetu možno formulovať aj takto:
Veta 5.1 . Ak sú všetky apotémy pyramídy rovnaké, potom je možné do základne takejto pyramídy vpísať kruh a výška znížená zhora k základni spadá do stredu kruhu vpísaného do základne.
Dokážme vetu na príklade štvorhrannej pyramídy. Nech je daná pyramída KABCD, K je vrchol, ABCD je základňa. Nakreslite výšku KO pyramídy. V každej bočnej ploche nakreslíme výšku od vrcholu pyramídy po stranu základne. V rovine podstavy spojíme bod O (základňa výšky) s bodom podôb týchto výšok - apotéma. OP, OT, OM a OE sú kolmé na AB, BC, CD a AD (veta o troch kolmiciach). Podľa definície sú uhly KRO, KTO, KMO, KEO lineárne uhly dihedrálnych uhlov medzi zodpovedajúcimi bočnými plochami a základňou ABCD. Výška KO je kolmá na základňu, preto je kolmá na akúkoľvek priamku v tejto rovine, t.j. kolmé na priamky OR, OT, OM a OE. To hovorí, že trojuholníky KRO, KTO, KMO, KEO sú pravouhlé.
Podľa podmienky (Veta 5) sú uhly KRO, KTO, KMO, KEO rovnaké. Zoberme si trojuholníky KRO, KTO, KMO, KEO, sú pravouhlé a rovnaké (pozdĺž nohy a ostrého uhla, KO - spoločný a uhly KRO, KTO, KMO, KEO sú rovnaké podľa podmienky).
Podľa podmienky (veta 5.1) sú KR, KT, KM a KE rovnaké, preto sú trojuholníky KRO, KTO, KMO, KEO pravouhlé a rovné v ramene a prepone.
Z rovnosti týchto trojuholníkov vyplýva, že ich strany OR, OT, OM a OE sú rovnaké, čo znamená, že v štvoruholníku ABCD je bod, ktorý je rovnako vzdialený od jeho strán, to znamená, že do neho možno vpísať kružnicu. .

Veta 6 . Ak sú všetky bočné okraje pyramídy naklonené k rovine základne pod rovnakým uhlom, potom je možné opísať kruh v blízkosti základne takejto pyramídy a výška znížená zhora na základňu klesá do stredu kruh opísaný v blízkosti základne.
Túto vetu možno formulovať aj takto:
Veta 6.1 . Ak sú všetky bočné okraje pyramídy rovnaké, potom môže byť kruh opísaný blízko základne takejto pyramídy a výška znížená zhora k základni klesá do stredu opísanej kružnice blízko základne.
Dokážme vetu na príklade štvorhrannej pyramídy. Nech je daná pyramída KABCD, K je vrchol, ABCD je základňa. Nakreslite výšku KO pyramídy. V rovine základne spojte bod O (základňu výšky) so všetkými vrcholmi základne A, B, C a D. Uhol KBO je uhol medzi hranou KB a rovinou základne (tj. uhol medzi priamkou a rovinou je uhol medzi touto priamkou a jej priemetom do tejto roviny) . Rovnakým spôsobom dokážeme, že uhly KSO, KAO a KDO sú uhly, ktoré zvierajú zodpovedajúce hrany KS, KA a KD so základnou rovinou. Výška KO je kolmá na základňu, preto je kolmá na akúkoľvek priamku v tejto rovine, t.j. kolmo na priamky OA, OB, OC a OD. To hovorí, že trojuholníky KAO, KBO, KCO, KDO sú pravouhlé.
Uhly KVO, KSO, KAO a KDO sú rovnaké (podľa podmienok vety 6). Zoberme si trojuholníky KAO, KBO, KCO, KDO, sú pravouhlé a rovnaké (pozdĺž nohy a ostrého uhla je KO spoločný a uhly KAO, KVO, KSO, KDO sú rovnaké podľa podmienky).
Na dôkaz vety 6.1 uvažujeme aj trojuholníky KAO, KBO, KCO, KDO, sú pravouhlé a rovné v ramene a prepone (KO - všeobecné, KA=KV=KS=KD podľa hypotézy vety).
Z rovnosti týchto trojuholníkov vyplýva, že ich príslušné strany OA, OB, OS a OD sú rovnaké, čo znamená, že na základni je bod, ktorý je rovnako vzdialený od vrcholov štvoruholníka ABCD, to znamená, že kruh možno opísať. okolo toho.

Pyramída sa nazýva mnohosten, ktorého jedna strana je mnohouholník ( základňu ) a všetky ostatné plochy sú trojuholníky so spoločným vrcholom ( bočné steny ) (obr. 15). Pyramída je tzv správne , ak je jeho základňa pravidelný mnohouholník a vrchol pyramídy sa premieta do stredu základne (obr. 16). Trojuholníková pyramída, v ktorej sú všetky hrany rovnaké, sa nazýva štvorsten .

Bočné rebro pyramída sa nazýva strana bočnej steny, ktorá nepatrí k základni Výška pyramída je vzdialenosť od jej vrcholu k rovine základne. Všetky bočné hrany pravidelnej pyramídy sú si navzájom rovné, všetky bočné strany sú rovnaké rovnoramenné trojuholníky. Výška bočnej plochy pravidelnej pyramídy vytiahnutej z vrcholu sa nazýva apotéma . diagonálny rez Časť pyramídy sa nazýva rovina prechádzajúca dvoma bočnými hranami, ktoré nepatria k tej istej ploche.

Bočná plocha povrchu pyramída sa nazýva súčet plôch všetkých bočných plôch. Celá plocha je súčet plôch všetkých bočných plôch a základne.

Vety

1. Ak sú v pyramíde všetky bočné hrany rovnako naklonené k rovine podstavy, potom sa vrchol pyramídy premieta do stredu opísanej kružnice blízko podstavy.

2. Ak v pyramíde majú všetky bočné hrany rovnakú dĺžku, potom sa vrchol pyramídy premieta do stredu opísanej kružnice blízko základne.

3. Ak sú v pyramíde všetky steny rovnako naklonené k rovine základne, potom sa vrchol pyramídy premieta do stredu kruhu vpísaného do základne.

Na výpočet objemu ľubovoľnej pyramídy je vzorec správny:

kde V- objem;

S hlavná- základná plocha;

H je výška pyramídy.

Pre pravidelnú pyramídu platia nasledujúce vzorce:

kde p- obvod základne;

h a- apotéma;

H- výška;

S plný

S strana

S hlavná- základná plocha;

V je objem pravidelnej pyramídy.

zrezaná pyramída nazývaná časť pyramídy uzavretá medzi základňou a reznou rovinou rovnobežnou so základňou pyramídy (obr. 17). Správna zrezaná pyramída nazývaná časť pravidelnej pyramídy, uzavretá medzi základňou a reznou rovinou rovnobežnou so základňou pyramídy.

základy zrezaná pyramída - podobné mnohouholníky. Bočné plochy - lichobežník. Výška zrezaná pyramída sa nazýva vzdialenosť medzi jej základňami. Uhlopriečka Zrezaný ihlan je segment spájajúci jeho vrcholy, ktoré neležia na rovnakej ploche. diagonálny rez Úsek zrezaného ihlana sa nazýva rovina prechádzajúca dvoma bočnými hranami, ktoré nepatria k tej istej ploche.

Pre skrátenú pyramídu platia tieto vzorce:

(4)

kde S 1 , S 2 - oblasti hornej a dolnej základne;

S plný je celková plocha povrchu;

S strana je plocha bočného povrchu;

H- výška;

V je objem zrezanej pyramídy.

Pre pravidelnú skrátenú pyramídu platí nasledujúci vzorec:

kde p 1 , p 2 - obvody základne;

h a- apotém pravidelnej zrezanej pyramídy.

Príklad 1 V pravidelnej trojuholníkovej pyramíde je dihedrálny uhol pri základni 60º. Nájdite dotyčnicu uhla sklonu bočnej hrany k rovine základne.

rozhodnutie. Urobme si nákres (obr. 18).

Pyramída je pravidelná, čo znamená, že základňa je rovnostranný trojuholník a všetky bočné strany sú rovnaké rovnoramenné trojuholníky. Dihedrálny uhol pri základni je uhol sklonu bočnej steny pyramídy k rovine základne. Lineárny uhol bude uhol a medzi dvoma kolmicami: t.j. Vrch pyramídy sa premieta do stredu trojuholníka (stred opísanej kružnice a kružnice vpísanej v trojuholníku ABC). Uhol sklonu bočného rebra (napr SB) je uhol medzi samotnou hranou a jej priemetom do základnej roviny. Pre rebro SB tento uhol bude uhol SBD. Ak chcete nájsť dotyčnicu, musíte poznať nohy SO a OB. Nechajte dĺžku segmentu BD je 3 a. bodka Oúsečka BD sa delí na časti: a Od nachádzame SO: Z toho nájdeme:

odpoveď:

Príklad 2 Nájdite objem pravidelného zrezaného štvorbokého ihlana, ak uhlopriečky jeho podstav sú cm a cm a výška je 4 cm.

rozhodnutie. Na zistenie objemu zrezanej pyramídy použijeme vzorec (4). Ak chcete nájsť oblasti základní, musíte nájsť strany základných štvorcov a poznať ich uhlopriečky. Strany podstavy sú 2 cm a 8 cm. To znamená plochy podstav a Nahradením všetkých údajov do vzorca vypočítame objem zrezaného ihlana:

odpoveď: 112 cm3.

Príklad 3 Nájdite plochu bočnej steny pravidelného trojuholníkového zrezaného ihlana, ktorého základné strany sú 10 cm a 4 cm a výška pyramídy je 2 cm.

rozhodnutie. Urobme si nákres (obr. 19).

Bočná strana tejto pyramídy je rovnoramenný lichobežník. Na výpočet plochy lichobežníka potrebujete poznať základy a výšku. Základy sú dané stavom, neznáma zostáva len výška. Nájdite to odkiaľ ALE 1 E kolmo od bodu ALE 1 v rovine spodnej základne, A 1 D- kolmý od ALE 1 na AC. ALE 1 E\u003d 2 cm, pretože toto je výška pyramídy. Na nájdenie DE urobíme dodatočný výkres, na ktorom znázorníme pohľad zhora (obr. 20). Bodka O- priemet stredov hornej a dolnej podstavy. keďže (pozri obr. 20) a Na druhej strane OK je polomer vpísanej kružnice a OM je polomer vpísanej kružnice:

MK=DE.

Podľa Pytagorovej vety z

Oblasť bočnej tváre:

odpoveď:

Príklad 4 Na základni pyramídy leží rovnoramenný lichobežník, ktorého základne a a b (a> b). Každá bočná plocha zviera uhol rovný rovine základne pyramídy j. Nájdite celkovú plochu pyramídy.

rozhodnutie. Urobme si nákres (obr. 21). Celková plocha pyramídy SABCD sa rovná súčtu plôch a plochy lichobežníka A B C D.

Použime tvrdenie, že ak sú všetky steny pyramídy rovnako naklonené k rovine podstavy, potom sa vrchol premieta do stredu kružnice vpísanej do podstavy. Bodka O- vrcholová projekcia S na základni pyramídy. Trojuholník SOD je ortogonálny priemet trojuholníka CSD do základnej roviny. Podľa vety o oblasti ortogonálnej projekcie plochej postavy dostaneme:

Podobne to znamená Problém sa teda zmenšil na nájdenie oblasti lichobežníka A B C D. Nakreslite lichobežník A B C D samostatne (obr. 22). Bodka O je stred kružnice vpísanej do lichobežníka.

Pretože kruh môže byť vpísaný do lichobežníka, potom alebo Podľa Pytagorovej vety máme