Gli angoli di inclinazione delle facce laterali della piramide. Piramide. Tronco di piramide. Per una piramide tronca regolare, la formula è vera

Considera le proprietà delle piramidi in cui le facce laterali sono perpendicolari alla base.

Se un due facce laterali adiacenti di una piramide sono perpendicolari alla base, poi il bordo laterale comune di queste facce è l'altezza della piramide. Se il compito lo dice il bordo della piramide è la sua altezza, quindi stiamo parlando di questo tipo di piramidi.

Le facce della piramide perpendicolari alla base sono triangoli rettangoli.

Se la base della piramide è un triangolo

La superficie laterale di tale piramide è generalmente ricercata come somma delle aree di tutte le facce laterali.

La base della piramide è una proiezione ortogonale di una faccia che non è perpendicolare alla base (in questo caso, SBC). Quindi, secondo il teorema dell'area di proiezione ortogonale, l'area di base è uguale al prodotto dell'area di questa faccia per il coseno dell'angolo tra essa e il piano di base.

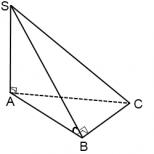
Se la base della piramide è un triangolo rettangolo

In questo caso tutte le facce della piramide sono triangoli rettangoli.

I triangoli SAB e SAC sono ad angolo retto, poiché SA è l'altezza della piramide. Il triangolo ABC è un triangolo rettangolo.

Il fatto che il triangolo SBC sia rettangolo deriva dal teorema su tre perpendicolari (AB è la proiezione dell'obliquo SB sul piano della base. Poiché AB è perpendicolare a BC dalla condizione, allora SB è anche perpendicolare a BC ).

L'angolo tra la faccia laterale dell'SBC e la base in questo caso è l'angolo dell'ABS.

L'area della superficie laterale è uguale alla somma delle aree dei triangoli rettangoli:

Poiché in questo caso

Se la base della piramide è un triangolo isoscele

In questo caso, l'angolo tra il piano della faccia laterale BCS e il piano della base è l'angolo AFS, dove AF è l'altitudine, mediana e bisettrice del triangolo isoscele ABC.

Allo stesso modo - se alla base della piramide si trova un triangolo equilatero ABC.

Se la base della piramide è un parallelogramma

In questo caso, la base della piramide è una proiezione ortogonale delle facce laterali che non sono perpendicolari alla base.

Se dividiamo la base in due triangoli, allora

dove α e β sono, rispettivamente, gli angoli tra i piani ADS e CDS e il piano di base.

Se BF e BK sono le altezze del parallelogramma, l'angolo BFS è l'angolo di inclinazione della faccia laterale CDS rispetto al piano di base e l'angolo BKS è l'angolo di inclinazione della faccia ADS.

(il disegno è fatto per il caso in cui B è un angolo ottuso).

Se la base della piramide è un rombo ABCD, gli angoli BFS e BKS sono uguali. Anche i triangoli ABS e CBS, così come ADS e CDS sono uguali in questo caso.

Se la base della piramide è un rettangolo

In questo caso, l'angolo tra il piano della faccia laterale SAD e il piano della base è l'angolo SAB,

e l'angolo tra il piano della faccia laterale SCD e il piano della base è l'angolo SCB

(dal teorema delle tre perpendicolari).

Ricordiamo: l'apotema è l'altezza della faccia laterale della piramide, disegnata dall'alto al bordo della base.
Teorema 5 . Se tutte le facce laterali della piramide sono inclinate rispetto al piano della base con lo stesso angolo, allora un cerchio può essere inscritto nella base di tale piramide e l'altezza abbassata dalla cima alla base cade nel centro di il cerchio inscritto nella base.
Questo teorema può anche essere formulato come segue:
Teorema 5.1 . Se tutti gli apotemi di una piramide sono uguali, allora un cerchio può essere inscritto nella base di tale piramide e l'altezza abbassata dall'alto alla base cade nel centro del cerchio inscritto nella base.
Dimostriamo il teorema usando l'esempio di una piramide quadrangolare. Sia data la piramide KABCD, K è la sommità, ABCD è la base. Disegna l'altezza del KO della piramide. In ciascuna faccia laterale, disegniamo un'altezza dalla sommità della piramide al lato della base. Nel piano della base, colleghiamo il punto O (la base dell'altezza) con il punto delle basi di queste altezze - apotema. OP, OT, OM e OE sono rispettivamente perpendicolari ad AB, BC, CD e AD (teorema delle tre perpendicolari). Per definizione, gli angoli KRO, KTO, KMO, KEO sono gli angoli lineari degli angoli diedri tra le facce laterali corrispondenti e la base ABCD. L'altezza di KO è perpendicolare alla base, quindi è perpendicolare a qualsiasi retta in questo piano, cioè perpendicolare alle rette OR, OT, OM e OE. Questo dice che i triangoli KRO, KTO, KMO, KEO sono rettangolari.
Per condizione (Teorema 5), ​​gli angoli KRO, KTO, KMO, KEO sono uguali. Considera i triangoli KRO, KTO, KMO, KEO, sono rettangolari e uguali (lungo la gamba e l'angolo acuto, KO è comune e gli angoli KRO, KTO, KMO, KEO sono uguali per condizione).
Per condizione (teorema 5.1) KR, KT, KM e KE sono uguali, quindi i triangoli KRO, KTO, KMO, KEO sono rettangolari e uguali in gamba e ipotenusa.
Dall'uguaglianza di questi triangoli deriva che i loro rispettivi lati OR, OT, OM e OE sono uguali, il che significa che c'è un punto nel quadrilatero ABCD che è equidistante dai suoi lati, cioè in esso può essere inscritta una circonferenza .

Teorema 6 . Se tutti i bordi laterali della piramide sono inclinati rispetto al piano della base con lo stesso angolo, allora un cerchio può essere descritto vicino alla base di tale piramide e l'altezza abbassata dalla cima alla base cade al centro di il cerchio descritto vicino alla base.
Questo teorema può anche essere formulato come segue:
Teorema 6.1 . Se tutti i bordi laterali della piramide sono uguali, allora un cerchio può essere circoscritto vicino alla base di tale piramide e l'altezza abbassata dall'alto alla base cade al centro del cerchio circoscritto vicino alla base.
Dimostriamo il teorema usando l'esempio di una piramide quadrangolare. Sia data la piramide KABCD, K è la sommità, ABCD è la base. Disegna l'altezza del KO della piramide. Nel piano della base, connetti il ​​punto O (la base dell'altezza) con tutti i vertici della base A, B, C e D. L'angolo KBO è l'angolo tra lo spigolo KB e il piano della base (il l'angolo tra la linea e il piano è l'angolo tra questa linea e la sua proiezione su questo piano) . Allo stesso modo dimostriamo che gli angoli KSO, KAO e KDO sono gli angoli formati dai corrispondenti spigoli KS, KA e KD con il piano di base. L'altezza di KO è perpendicolare alla base, quindi è perpendicolare a qualsiasi retta in questo piano, cioè perpendicolare alle linee OA, OB, OC e OD. Questo dice che i triangoli KAO, KBO, KCO, KDO sono rettangolari.
Gli angoli KVO, KSO, KAO e KDO sono uguali (per le condizioni del Teorema 6). Considera i triangoli KAO, KBO, KSO, KDO, sono rettangolari e uguali (lungo la gamba e l'angolo acuto, KO è comune e gli angoli KAO, KVO, KSO, KDO sono uguali per condizione).
Dimostrando il Teorema 6.1, consideriamo anche i triangoli KAO, KBO, KCO, KDO, sono rettangolari e uguali in gamba e ipotenusa (KO - comune, KA=KV=KS=KD per la condizione del teorema).
Dall'uguaglianza di questi triangoli deriva che i loro rispettivi lati OA, OB, OS e OD sono uguali, il che significa che c'è un punto alla base che è equidistante dai vertici del quadrilatero ABCD, cioè si può circoscrivere un cerchio intorno ad esso.

Piramideè chiamato poliedro, una delle cui facce è un poligono ( base ), e tutte le altre facce sono triangoli con un vertice comune ( facce laterali ) (Fig. 15). La piramide si chiama corretta , se la sua base è un poligono regolare e la sommità della piramide è proiettata al centro della base (Fig. 16). Si chiama piramide triangolare in cui tutti gli spigoli sono uguali tetraedro .

Costata laterale piramide è chiamato il lato della faccia laterale che non appartiene alla base Altezza piramide è la distanza dalla sua sommità al piano della base. Tutti gli spigoli laterali di una piramide regolare sono uguali tra loro, tutte le facce laterali sono triangoli isoscele uguali. Si chiama l'altezza della faccia laterale di una piramide regolare disegnata dal vertice apotema . sezione diagonale Una sezione di una piramide è chiamata piano passante per due spigoli laterali che non appartengono alla stessa faccia.

Superficie laterale piramide è chiamata la somma delle aree di tutte le facce laterali. Piena superficie è la somma delle aree di tutte le facce laterali e della base.

Teoremi

1. Se in una piramide tutti i bordi laterali sono ugualmente inclinati rispetto al piano della base, la sommità della piramide viene proiettata nel centro del cerchio circoscritto vicino alla base.

2. Se in una piramide tutti i bordi laterali hanno la stessa lunghezza, la sommità della piramide viene proiettata nel centro del cerchio circoscritto vicino alla base.

3. Se nella piramide tutte le facce sono ugualmente inclinate rispetto al piano della base, la sommità della piramide viene proiettata nel centro del cerchio inscritto nella base.

Per calcolare il volume di una piramide arbitraria, la formula è corretta:

dove V- volume;

S principale- superficie di base;

Hè l'altezza della piramide.

Per una piramide regolare, valgono le seguenti formule:

dove p- il perimetro della base;

h a- apotema;

H- altezza;

S pieno

lato S

S principale- superficie di base;

Vè il volume di una piramide regolare.

tronco di piramide detta parte della piramide racchiusa tra la base ed il piano di taglio parallelo alla base della piramide (Fig. 17). Corretta piramide tronca detta parte di una piramide regolare, racchiusa tra la base ed un piano di taglio parallelo alla base della piramide.

Fondamenti tronco di piramide - poligoni simili. Facce laterali - trapezio. Altezza tronco piramidale si chiama distanza tra le sue basi. Diagonale Una piramide tronca è un segmento che collega i suoi vertici che non giacciono sulla stessa faccia. sezione diagonale Una sezione di una piramide tronca è chiamata piano passante per due spigoli laterali che non appartengono alla stessa faccia.

Per una piramide tronca valgono le formule:

(4)

dove S 1 , S 2 - aree delle basi superiore e inferiore;

S pienoè la superficie totale;

lato Sè la superficie laterale;

H- altezza;

Vè il volume della piramide tronca.

Per una piramide tronca regolare, vale la seguente formula:

dove p 1 , p 2 - perimetri di base;

h a- l'apotema di una piramide tronca regolare.

Esempio 1 In una piramide triangolare regolare, l'angolo diedro alla base è di 60º. Trova la tangente dell'angolo di inclinazione del bordo laterale al piano della base.

Decisione. Facciamo un disegno (Fig. 18).

La piramide è regolare, il che significa che la base è un triangolo equilatero e tutte le facce laterali sono triangoli isoscele uguali. L'angolo diedro alla base è l'angolo di inclinazione della faccia laterale della piramide rispetto al piano della base. L'angolo lineare sarà l'angolo un tra due perpendicolari: cioè La sommità della piramide è proiettata al centro del triangolo (il centro del cerchio circoscritto e il cerchio inscritto nel triangolo ABC). L'angolo di inclinazione della nervatura laterale (ad es SB) è l'angolo tra il bordo stesso e la sua proiezione sul piano di base. Per costolette SB questo angolo sarà l'angolo SBD. Per trovare la tangente devi conoscere le gambe COSÌ e OB. Lascia la lunghezza del segmento BDè 3 un. punto o segmento BDè diviso in parti: e Da troviamo COSÌ: Da troviamo:

Risposta:

Esempio 2 Trova il volume di una piramide tronca quadrangolare regolare se le diagonali delle sue basi sono cm e cm e l'altezza è 4 cm.

Decisione. Per trovare il volume di una piramide tronca, utilizziamo la formula (4). Per trovare le aree delle basi, devi trovare i lati dei quadrati delle basi, conoscendone le diagonali. I lati delle basi sono rispettivamente di 2 cm e 8 cm Questo significa le aree delle basi e Sostituendo tutti i dati nella formula, calcoliamo il volume della piramide tronca:

Risposta: 112 cm3.

Esempio 3 Trova l'area della faccia laterale di una piramide tronca triangolare regolare i cui lati delle basi sono 10 cm e 4 cm e l'altezza della piramide è 2 cm.

Decisione. Facciamo un disegno (Fig. 19).

La faccia laterale di questa piramide è un trapezio isoscele. Per calcolare l'area di un trapezio, devi conoscere le basi e l'altezza. Le basi sono date dalla condizione, solo l'altezza rimane sconosciuta. Trovalo da dove MA 1 e perpendicolare a un punto MA 1 sul piano della base inferiore, UN 1 D- perpendicolare da MA 1 su corrente alternata. MA 1 e\u003d 2 cm, poiché questa è l'altezza della piramide. Per trovare DE faremo un disegno aggiuntivo, in cui rappresenteremo una vista dall'alto (Fig. 20). Punto o- proiezione dei centri delle basi superiore e inferiore. poiché (vedi Fig. 20) e D'altra parte OKè il raggio del cerchio inscritto e OMè il raggio del cerchio inscritto:

MK=DE.

Secondo il teorema di Pitagora di

Area del viso laterale:

Risposta:

Esempio 4 Alla base della piramide giace un trapezio isoscele, le cui basi un e b (un> b). Ciascuna faccia laterale forma un angolo uguale al piano della base della piramide j. Trova la superficie totale della piramide.

Decisione. Facciamo un disegno (Fig. 21). Superficie totale della piramide SABCDè uguale alla somma delle aree e dell'area del trapezio ABCD.

Usiamo l'affermazione che se tutte le facce della piramide sono ugualmente inclinate rispetto al piano della base, allora il vertice è proiettato nel centro del cerchio inscritto nella base. Punto o- proiezione dei vertici S alla base della piramide. Triangolo ZOLLA ERBOSAè la proiezione ortogonale del triangolo CSD al piano di base. Secondo il teorema sull'area della proiezione ortogonale di una figura piatta, otteniamo:

Allo stesso modo, significa Pertanto, il problema si è ridotto a trovare l'area del trapezio ABCD. Disegna un trapezio ABCD separatamente (Fig. 22). Punto oè il centro di un cerchio inscritto in un trapezio.

Poiché un cerchio può essere inscritto in un trapezio, allora o Per il teorema di Pitagora abbiamo